The complex that exists as a pair of enantiomers is
(a) trans−[Co(H2NCH2CH2CNH2)2Cl2]+
(b) [Co(H2NCH2CH2NH2)3]3+
(c) [Pt(PPh3)(Cl)(Br)(CH3)]−
(d) cis−[CoNH3)4Cl2]+
The correct Answer is:B
To determine which complex exists as a pair of enantiomers, we need to analyze the given options based on the criteria for optical activity and the presence of a plane of symmetry (PoS). Enantiomers are non-superimposable mirror images, and for a complex to be optically active, it must lack any symmetry elements that would make it superimposable on its mirror image.
1. Understanding Enantiomers:
- Enantiomers are pairs of molecules that are mirror images of each other but cannot be superimposed. For a complex to exhibit enantiomerism, it must be optically active, meaning it does not have a plane of symmetry.
2. Analyzing the First Option (trans-Co(en)₂Cl₂⁺):
- The structure of trans-Co(en)₂Cl₂⁺ can be drawn, where "en" represents ethylenediamine ligands.
- In this case, if we draw the structure, we find that there is a plane of symmetry present. Thus, this complex is not optically active and does not exist as enantiomers.
3. Analyzing the Second Option ((Co(en)₃)³⁺):
- For (Co(en)₃)³⁺, we can visualize the arrangement of the ligands.
- Since the ethylenediamine ligands are arranged in a way that does not allow for a plane of symmetry, this complex is optically active. Therefore, it can exist as a pair of enantiomers.
4. Analyzing the Third Option (Square planar Pt complex):
- In the square planar complex with platinum, if we draw the structure, we notice that there is a plane of symmetry present. Thus, this complex is also not optically active and does not exhibit enantiomerism.
5. Analyzing the Fourth Option (Cobalt complex with Cl and NH₃):
- For the cobalt complex with Cl and NH₃, when we draw the structure, we find that there is a plane of symmetry. Therefore, this complex is not optically active and does not exist as enantiomers.
6. Conclusion:
- Based on the analysis, the only complex that exists as a pair of enantiomers is (Co(en)₃)³⁺.
Final Answer:
The complex that exists as a pair of enantiomers is (Co(en)₃)³⁺.
- Enantiomers are pairs of molecules that are mirror images of each other but cannot be superimposed. For a complex to exhibit enantiomerism, it must be optically active, meaning it does not have a plane of symmetry.
- The structure of trans-Co(en)₂Cl₂⁺ can be drawn, where "en" represents ethylenediamine ligands.
- In this case, if we draw the structure, we find that there is a plane of symmetry present. Thus, this complex is not optically active and does not exist as enantiomers.
- For (Co(en)₃)³⁺, we can visualize the arrangement of the ligands.
- Since the ethylenediamine ligands are arranged in a way that does not allow for a plane of symmetry, this complex is optically active. Therefore, it can exist as a pair of enantiomers.
- In the square planar complex with platinum, if we draw the structure, we notice that there is a plane of symmetry present. Thus, this complex is also not optically active and does not exhibit enantiomerism.
- For the cobalt complex with Cl and NH₃, when we draw the structure, we find that there is a plane of symmetry. Therefore, this complex is not optically active and does not exist as enantiomers.
- Based on the analysis, the only complex that exists as a pair of enantiomers is (Co(en)₃)³⁺.
The complex that exists as a pair of enantiomers is (Co(en)₃)³⁺.
Topper's Solved these Questions
- COORDINATION COMPOUNDSBOOK - A2ZCHAPTER - COORDINATION COMPOUNDSEXERCISE - Wemer Theory And Vbt
42 Videos
- COORDINATION COMPOUNDSBOOK - A2ZCHAPTER - COORDINATION COMPOUNDSEXERCISE - Crystal Field Theory (Cft)
16 Videos
- COORDINATION COMPOUNDSBOOK - A2ZCHAPTER - COORDINATION COMPOUNDSEXERCISE - Structural Isomerism
31 Videos
- CHEMICAL KINETICSBOOK - A2ZCHAPTER - CHEMICAL KINETICSEXERCISE - Section D - Chapter End Test
30 Videos
- ELECTROCHEMISTRYBOOK - A2ZCHAPTER - ELECTROCHEMISTRYEXERCISE - Section D - Chapter End Test
30 Videos
Similar Questions
Knowledge Check
Enantiomers are
Amolecule that have at least one chiral carbonBnon-superimposible molecules that are mirror images of one anotherCnon-superimposible constitutional isomersDnon-superimposible moleculesThe two projection formulae that represent a pair of enantiomers are.
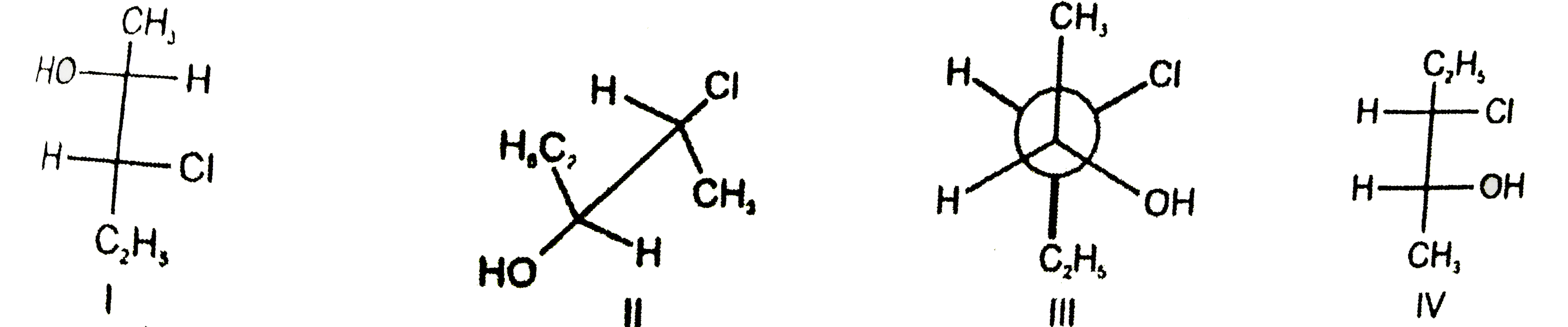 AI and IIBIII and IVCI and IIIDII and IV
AI and IIBIII and IVCI and IIIDII and IVEnantiomers have
Aidentical melting point/boiling point but different refractive indicesBidentical melting point/boiling point and refractive indices but rotate plane polarised light in opposite directions but to the same extentCdifferent refractive indices and rotate plane polarized light in the same direction but to different extentsDdifferent melting/boiling points but rotate plane of polarised light in diferent directions but to the same extents.
Which is not the pair of enantiomers ?
View SolutionEnantiomers have:
View SolutionWhich of the following compounds can exist both as a cis pair of enantiomers and a trans pair of enantiomers?
View SolutionThe following represents a pair of enantiomers:
View SolutionWhich of the following complexes will give a pair of enantiomers ?
View Solution

