The value of Δ0 for RhCl3−6 is 243kJ/mol what wavelength of light will promote an electron from. The colour of the complex is
(a) Blue
(b) Green
(c) Yellow
(d) Orange
The correct Answer is:D
Δ0RhCl−36 is 243kJ/mol
E=hcλ
λ=6.626×10−34×3×108234×103
=511nm. Nearest color is orange.
Topper's Solved these Questions
- COORDINATION COMPOUNDSBOOK - A2ZCHAPTER - COORDINATION COMPOUNDSEXERCISE - Metal Carbonyls, Stability Of Complexes And Applications
23 Videos
- COORDINATION COMPOUNDSBOOK - A2ZCHAPTER - COORDINATION COMPOUNDSEXERCISE - Section B - Assertion Reasoning
15 Videos
- COORDINATION COMPOUNDSBOOK - A2ZCHAPTER - COORDINATION COMPOUNDSEXERCISE - Wemer Theory And Vbt
42 Videos
- CHEMICAL KINETICSBOOK - A2ZCHAPTER - CHEMICAL KINETICSEXERCISE - Section D - Chapter End Test
30 Videos
- ELECTROCHEMISTRYBOOK - A2ZCHAPTER - ELECTROCHEMISTRYEXERCISE - Section D - Chapter End Test
30 Videos
Similar Questions
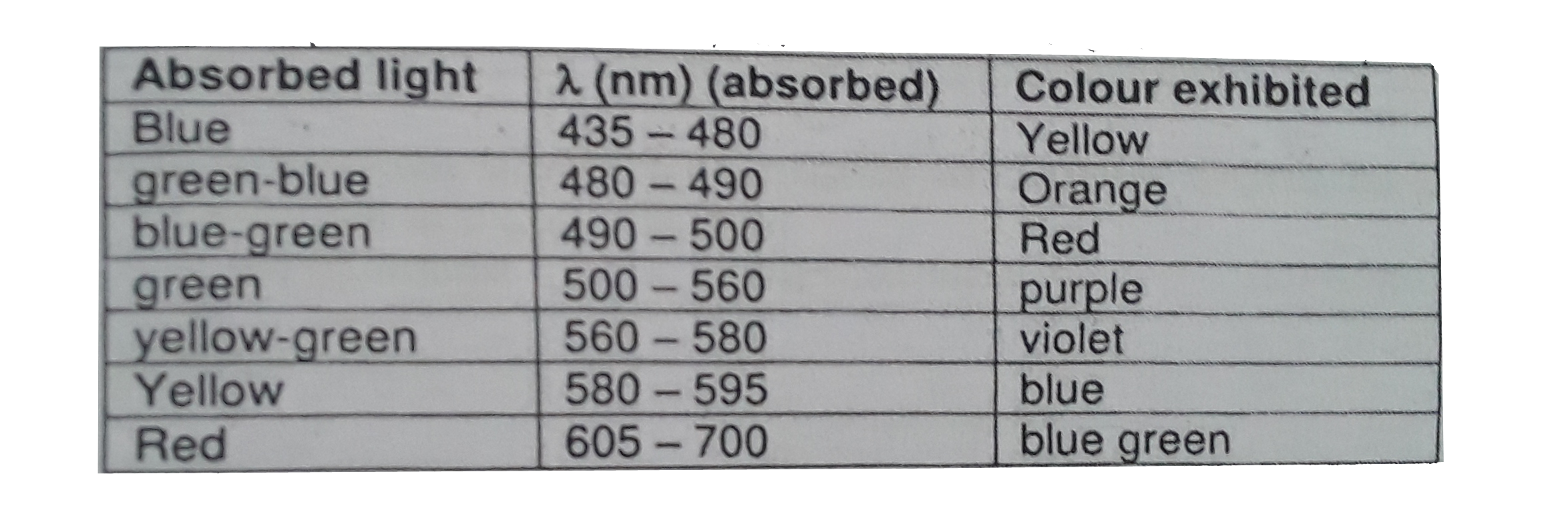
The value of Δ0 for [Ti(H2O)6]3+ is found to be 240 kJ mol−1 then predict the colour of the complex using the following table . (h=6×10−34J−sec,NA=6×1023c=3×108m/sec)
View SolutionIf the energy difference between the electronic states is 214.68kJmol−1, calculate the frequency of light emited when an electron drop form the height to the lower state. Planck's constant , h=39.79×10−14kJsmol−1
View Solution
Knowledge Check
Crystal field theory views the bonding in complexes as arising from electrostatic interaction and considers the effect of the ligand charges on the energies of the metal ion d-orbitals
In this theory, a ligand lone pair is modelled as a point negative charge that repels electrons in the d-orbitals of the central metal ion.The theory concentrated on the resulting splitting of the d-orbitals in two groups with different energies and used that splitting to rationalize and correlate the optical spectra,thermodynamic stability, and magnetic properties of complexes.This energy splitting between the two sets of d-orbitals is called the crystal field splitting Δ.
In general, the crystal field splitting energy Δ corresponds to wavelenght of light in visible region of the spectrum, and colours of the complexes can therefore be attributed to electronic transition between the lower and higher energy sets of d-orbitals.
In general, the colour that we see is complementry to the colour absorbed.

Different metal ions have different value of Δ, which explains why their complexes with the same ligand have different colour.
Similarly the crystal field splitting also depends on the nature of ligands and as the ligand for the same metal varies from H2O to NH3 to ethylenediamine, Δ for complexes increase.Accordingly, the electronic transition shifts to higher energy (shorter wavelength) as the ligand varies from H2O from NH3 to en, thus accounting for the variation in colour.
Crystal field theory accounts for the magnetic properties of complexes in terms of the relative values of Δ and the spin pairing energy P. Small Δ values favour high spin complexes, and large Δ values favour low spin complexes.
The [Ti(NCS)6]3− ion exhibits a single absorption band at 544 nm.What will be the crystal field splitting energy (in kJ mol−1) of the complex ? (h=6.626×10−34J.s,C=3.0×105m/s,NA=6.02×1023 ions/mole.A240B220C270D250The first ionization energy of Na is 495.9 kJ mol−1 . What is the longest wavelength of light that could remove an electron from a Na-atom?
A2.41×10−7mB2.41×10−4mC4.14 mD4.14×103mSplitting energy (Δ0) can usually be measured form the absorption spectra of the complex ions. In simple cases when light is absorbed by a complex ion, an electron in one of the lower energy orbitals is excited to one of the higher energy orbital. The energy corresponding to the frequency of absorbed light is equal to Δ0. If value of Δ0 for the complex is in visible region, the complex is coloured and the value of Δ0 lies in ultraviolet or infrared region, the complex is colourless. For octahedral complexes, the cyrstal field stabilisation energy is given by CFSE=+[−0.4t2gN+0.6egN1]Δ0 Where N and N1 are number of electrons in t2g and eg orbitals respectively.
The value of CFSE can be used for the correction of the experimental values of heats of hydration of divalent can be obtained by substracting the calculated CFSE values form the experimental values.
The value of crystal field splitting (Δ0) for [Ti(H2O)3+6 is 243 kj mol−1. The crystal field stabilisation energy (CFSE) in this complex is : (in kj mol−1)A−35×243B−25×243C−3×25×243D−243
The energy difference between two electronic states is 399.1 kJ mol−1. Calculate the wavelength and frequency of light emitted when an electron drops from a higher to a lower state. (Planck's constant, h=3.98×10−13kJmol−1).
View SolutionSplitting energy (Δ0) can usually be measured form the absorption spectra of the complex ions. In simple cases when light is absorbed by a complex ion, an electron in one of the lower energy orbitals is excited to one of the higher energy orbital. The energy corresponding to the frequency of absorbed light is equal to Δ0. If value of Δ0 for the complex is in visible region, the complex is coloured and the value of Δ0 lies in ultraviolet or infrared region, the complex is colourless. For octahedral complexes, the cyrstal field stabilisation energy is given by CFSE=+[−0.4t2gN+0.6egN1]Δ0 Where N and N1 are number of electrons in t2g and eg orbitals respectively.
The value of CFSE can be used for the correction of the experimental values of heats of hydration of divalent can be obtained by substracting the calculated CFSE values form the experimental values.
The value of crystal field splitting (Δ0) for [Ti(H2O)3+6 is 243 kj mol−1. The crystal field stabilisation energy (CFSE) in this complex is : (in kj mol−1)
View SolutionSplitting energy (Δ0) can usually be measured form the absorption spectra of the complex ions. In simple cases when light is absorbed by a complex ion, an electron in one of the lower energy orbitals is excited to one of the higher energy orbital. The energy corresponding to the frequency of absorbed light is equal to Δ0. If value of Δ0 for the complex is in visible region, the complex is coloured and the value of Δ0 lies in ultraviolet or infrared region, the complex is colourless. For octahedral complexes, the cyrstal field stabilisation energy is given by CFSE=+[−0.4t2gN+0.6egN1]Δ0 Where N and N1 are number of electrons in t2g and eg orbitals respectively.
The value of CFSE can be used for the correction of the experimental values of heats of hydration of divalent can be obtained by substracting the calculated CFSE values form the experimental values.
Which of the following statements is correct ?
View SolutionSplitting energy (Δ0) can usually be measured form the absorption spectra of the complex ions. In simple cases when light is absorbed by a complex ion, an electron in one of the lower energy orbitals is excited to one of the higher energy orbital. The energy corresponding to the frequency of absorbed light is equal to Δ0. If value of Δ0 for the complex is in visible region, the complex is coloured and the value of Δ0 lies in ultraviolet or infrared region, the complex is colourless. For octahedral complexes, the cyrstal field stabilisation energy is given by CFSE=+[−0.4t2gN+0.6egN1]Δ0 Where N and N1 are number of electrons in t2g and eg orbitals respectively.
The value of CFSE can be used for the correction of the experimental values of heats of hydration of divalent can be obtained by substracting the calculated CFSE values form the experimental values.
Which of the following statements is correct ?
View SolutionSplitting energy (Δ0) can usually be measured form the absorption spectra of the complex ions. In simple cases when light is absorbed by a complex ion, an electron in one of the lower energy orbitals is excited to one of the higher energy orbital. The energy corresponding to the frequency of absorbed light is equal to Δ0. If value of Δ0 for the complex is in visible region, the complex is coloured and the value of Δ0 lies in ultraviolet or infrared region, the complex is colourless. For octahedral complexes, the cyrstal field stabilisation energy is given by CFSE=+[−0.4t2gN+0.6egN1]Δ0 Where N and N1 are number of electrons in t2g and eg orbitals respectively.
The value of CFSE can be used for the correction of the experimental values of heats of hydration of divalent can be obtained by substracting the calculated CFSE values form the experimental values.
The heat of hydration of Cr2+ ion is −450k cal/mol. For [Cr(H2O)6]2+,Δ0=13,900 cm(−1). What heat of hydration would be, if there were no crystal field stabilisation energy ?
View Solution
