समचतुर्भुज ABCD में सिद्ध कीजिये कि AC2+BD2=4AB2
Step by step video & image solution for समचतुर्भुज ABCD में सिद्ध कीजिये कि AC^2+BD^2=4AB^2 by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - NOOTAN HINDICHAPTER - त्रिभुज EXERCISE - एन0 सी0 आर0 टी0 प्रश्न (प्रश्नावली 6.1)3videos
त्रिभुज
- BOOK - NOOTAN HINDICHAPTER - त्रिभुज EXERCISE - एन0 सी0 आर0 टी0 प्रश्न (प्रश्नावली 6.2)10videos
त्रिभुज
- BOOK - NOOTAN HINDICHAPTER - त्रिभुज EXERCISE - प्रश्नावली 6C11videos
त्रिभुज
- BOOK - NOOTAN HINDICHAPTER - त्रिकोणमिति के कुछ अनुप्रयोग EXERCISE - विविध प्रश्नावली (दीर्घ उतरिये प्रश्न)6videos
त्रिकोणमिति के कुछ अनुप्रयोग
- BOOK - NOOTAN HINDICHAPTER - दो चर वाले रैखिक समीकरण युग्म EXERCISE - विविध प्रश्नावली (बहुविकल्पीय प्रश्न)7videos
दो चर वाले रैखिक समीकरण युग्म
Similar Questions
कोष्ठकों में दिया शब्दों में से सही शब्दों का प्रयोग करते हुए , रिक्त स्थानों को भरिये
(i) सभी वृत्त ............... होते है (सर्वांगसम , समरूप )
(ii) सभी वर्ग ............... होते है
(iii) सभी ............... त्रिभुज समरूप होते है ( समद्विबाहु , समबाहु )
(iv) भुजाओ की समान संख्या वाले दो बहुभुज समरूप होते है , यदि (a) उनके संगत कोण ............... हो तथा (b) उनकी संगत भुजाएँ ............... हो ( बराबर, समानुपाती )06:13View Solutionआकृति (i) और (ii) में , DE || BC है (i) में EC और (ii) में AD ज्ञात कीजिये
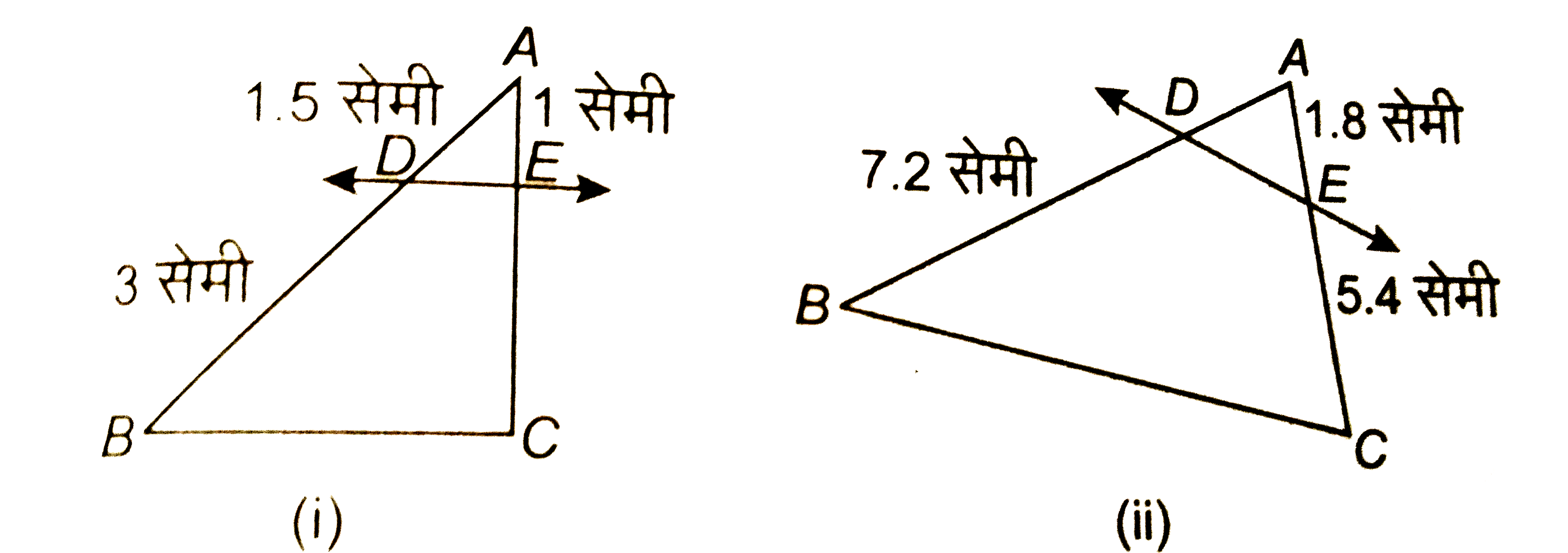
03:01View Solutionमान लीजिये ΔABC~ΔPQR है और इनके क्षेत्रफल क्रमशः 64 सेमी2 और 121 सेमी2 है यदि QR=15.4 सेमी2 हो तो BC ज्ञात कीजिए
04:22View Solutionकिसी सीधी क्षैतिज सड़क के ऊपर एक हवाई जहाज क्रमागत किलोमीटर के दो पत्थरों के बीच उड़ रहा है। ये पत्थर हवाई जहाज के दोनों ओर स्थित हैं। हवाई जहाज से पत्थरों के अवनतांश 30∘ और 60∘ हैं। सड़क से वायुयान की ऊँचाई मीटर में ज्ञात कीजिए।
04:35View Solutionसमीकरण 5x−15y=16 और 3x−9y=485 के युग्म का के हल होंगे :
02:36View SolutionABCD is a trapezium in which AB||CD then AC^(2)+BD^(2) is equal to
03:30View SolutionIn rhombus ABCD, show that 4AB2=AC2+BD2
02:48View SolutionIn the parallelogram ABCD,vec AC^(2)-vec BD^(2)=
02:43View SolutionABCD is a parallelogram Fig. 2 (c ) .64. ACand(BD)areitsdiagonals.Showtˆ<br> (a) vec (AC) +vec (BD) =2 vec (BC)<br>(b)vec (AC) - vec (BD) =2 vec (AB)
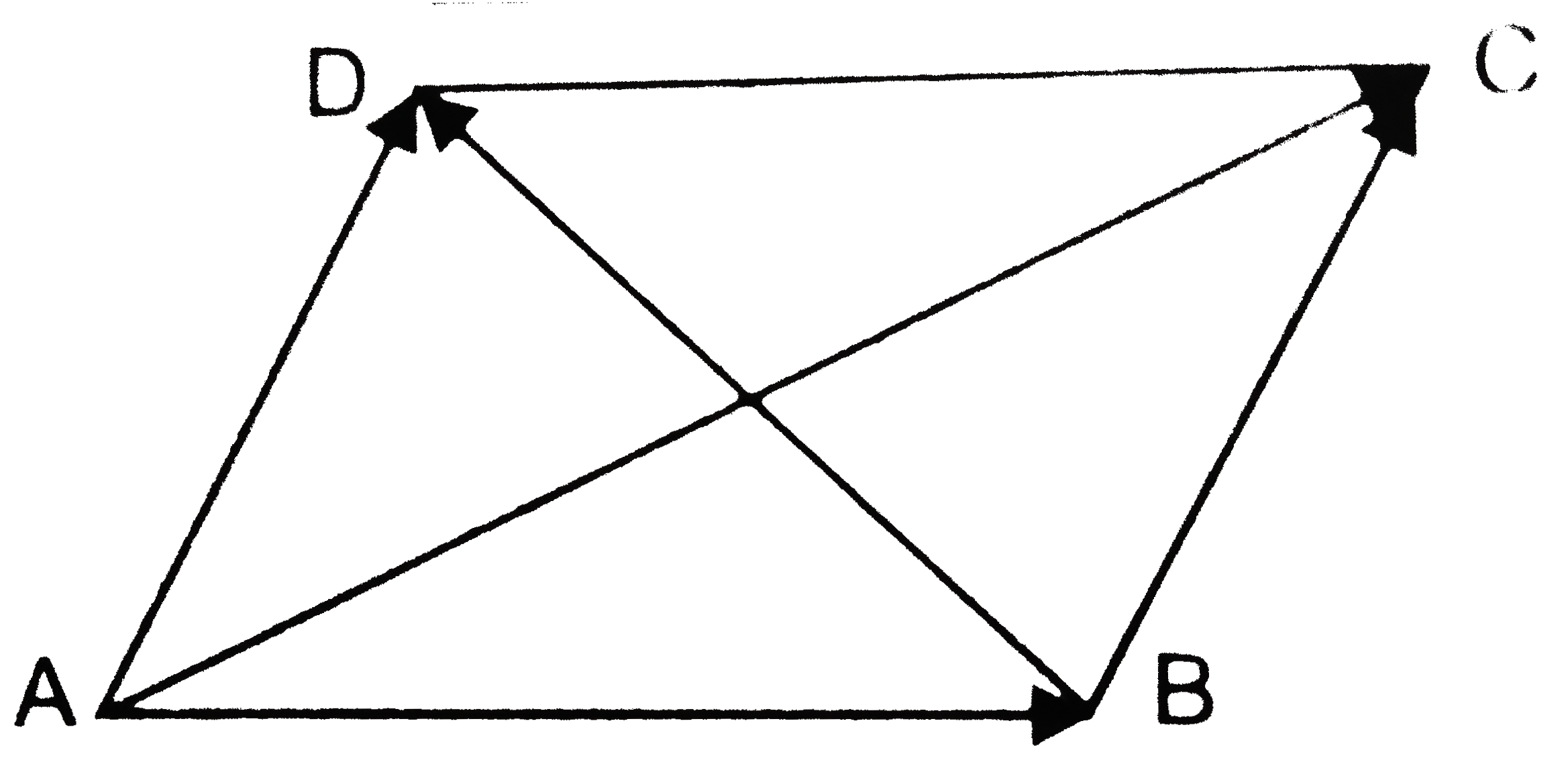. 02:12View SolutionIn a rhombus ABCD, prove that AC2+BD2=4AB2
03:31View SolutionIn the parallelogram ABCD, ¯¯¯¯¯¯AC2−¯¯¯¯¯¯BD2 =
03:47View Solutionकिसी समांतर चतुर्भुज ABCD में यदि −−→AB=¯a तथा −−→BC=¯b तो सिद्ध कीजिए कि
−−→AC=¯a+¯b और −−→BD=¯b−¯a.02:34View Solutionसिद्ध कीजिये कि (0,2π) में फलन f(x)=x−sinx वर्धमान है।
01:58View Solutionसिद्ध कीजिये कि प्रदत फलन f(x)=cosx
(0, pi) में निरंतर हस्यमान है।05:22View Solutionसिद्ध कीजिये कि3−2√5 एक अपरिमेय संख्या है।
05:26View Solution