बिंदु P(h, k) एक रेखा के अक्षो के बिच कटे अन्त:खण्ड को 1 : 2 के अनुपात में विभाजित करता है । इस रेखाखण्ड द्वारा अक्षो के बिच कटे अन्त:खण्ड कि लम्बाई ज्ञात कीजिए । इस रेखाखण्ड और अक्षो द्वारा बने त्रिभुज का क्षेत्रफल भी ज्ञात कीजिए ।
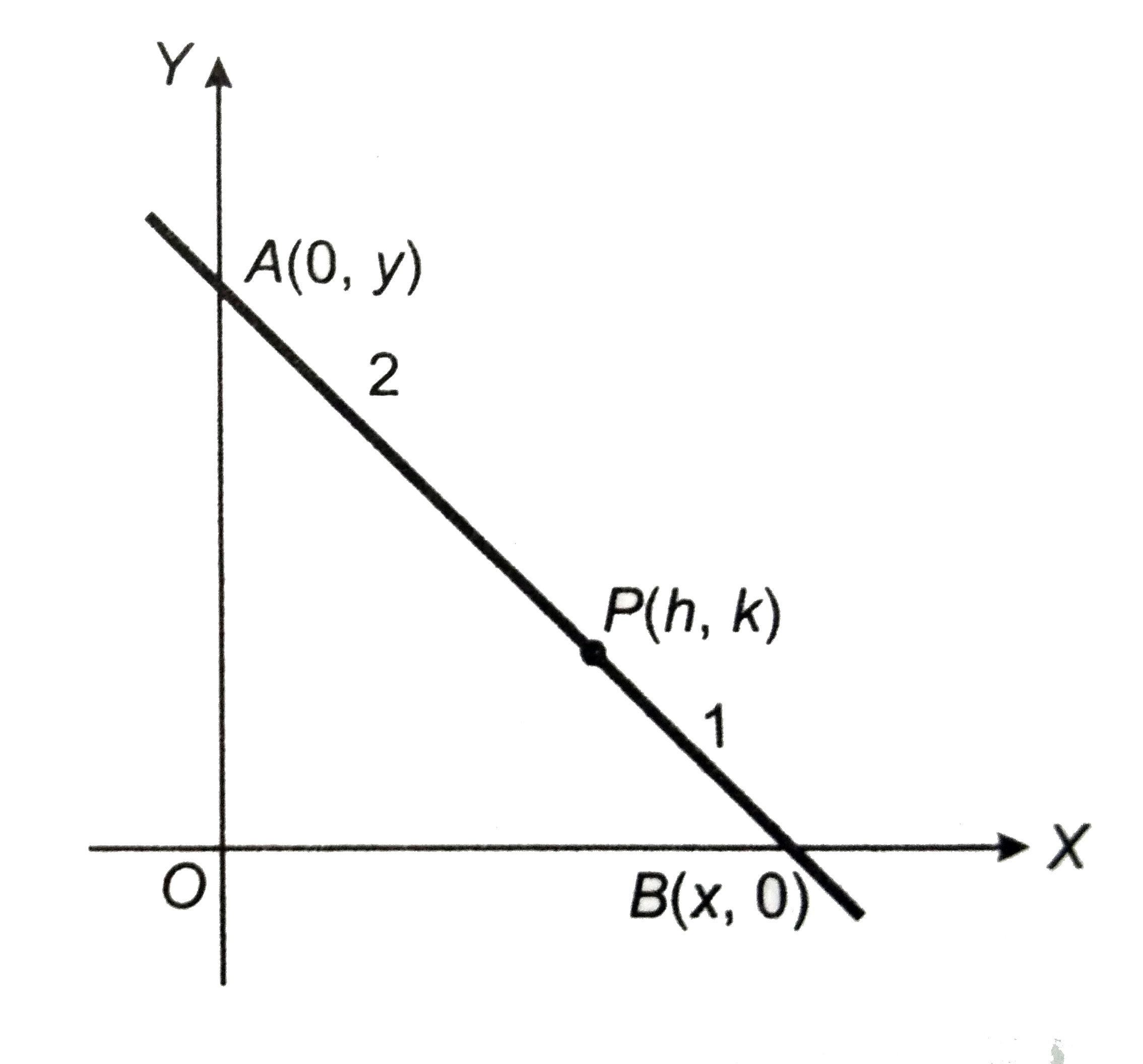
माना अक्षो के बीच रेखाखण्ड AB है जहाँ A≡(0,y) और B≡(x,0) है । P(h, k) एक रेखाखण्ड को 1 : 2 के अनुपात में विभाजित करता है ।
अब प्रश्न है कि PA : PB = 1 : 2
या PB : PA = 1 : 2
इसका उत्तर यह है कि अनुपात का प्रथम भाग सदैव X-अक्ष तथा दूसरा सदैव Y-अक्ष कि ओर से लिया जाता है ।
∴ यहाँ PB : PA = 1 : 2
∴ विभाजन सूत्र से,
h=1(0)+2(x)1+2 ⇒ h=2x3 ⇒ x=3h2
और k=1(y)+2(0)1+2 ⇒ k=y3 ⇒ y=3k
X-अक्ष पर कटे अन्त: खण्ड कि लम्बाई =OB=x=3h2
और Y-अक्ष पर कटे अन्त: खण्ड कि लम्बाई = OA = y = 3k.
∴ΔAOB का क्षेत्रफल =12×OB×OA=12×3h2×3k=94hk वर्ग मात्रक
Topper's Solved these Questions
- निर्देशांक ज्यामितिBOOK - NOOTAN HINDICHAPTER - निर्देशांक ज्यामितिEXERCISE - विविध उदाहरण
8 Videos
- निर्देशांक ज्यामितिBOOK - NOOTAN HINDICHAPTER - निर्देशांक ज्यामितिEXERCISE - प्रश्नावली 7 A
21 Videos
- द्विघात समीकरण BOOK - NOOTAN HINDICHAPTER - द्विघात समीकरण EXERCISE - विविध प्रश्नावली (बहुविकल्पीय प्रश्न)
7 Videos
- पृष्ठीय क्षेत्रफल और आयतन BOOK - NOOTAN HINDICHAPTER - पृष्ठीय क्षेत्रफल और आयतन EXERCISE - बहुविकल्पीय प्रश्न
7 Videos
Similar Questions
यदि बिंदु P(k - 1, 2) बिन्दुओ A(3, k) और B(k, 5) से समदूरस्थ है, तो k का मान ज्ञात कीजिए ।
View Solutionनिम्नलिखित बिंदु युग्मो के बीच की दूरी ज्ञात कीजिए :
(i) A(-6, 4) और B(2, -2)
(ii) A(-5, -1) और B(0, 4)
(iii) A(4, -1) और B(7, 3)
(iv) A(3, 4) और B(5, 2)
(v) A(4, 5) और B(-2, 5)
(vi) A(3, -4) और B(7, 0)
View Solutionनिम्नलिखित प्रश्न में चार विकल्प दिए गए हैं। उस विकल्प को चुनकर अपनी उत्तर पुस्तिका में लिखिए जिसके मूल वास्तविक हैं:
View Solutionएक सुराही निम्नलिखित का संयोजन है :
View Solutionदीर्घवृत्त x2+2y2=2 पर बाह्य बिंदु से खींची गयी स्पर्शियो के अक्षो के बीच कटे अन्तः खण्ड के मध्य - बिंदुओं का पथ होगा :
View Solutionरेखा 4x+3y=12 अक्षो को बिन्दुओ L और M पर प्रतिच्छेद करती है बिंदु इस प्रकार गति करता है की त्रिभुज PLM का क्षेत्रफल सदैव वर्ग इकाई रहता है , तो P का बिन्दुपथ ज्ञात कीजिये
View Solutionरेखाखण्ड AB अक्षो के बीच इस प्रकर गति करता है की A सदैव Y-अक्ष पर तथा B सदैव X- अक्ष पर हो । रेखाखण्ड AB पर एक बिंदु P इस प्रकार है की PA =a और PB =b यदि AB=a+b हो , तो बिंदु P का बिन्दुपथ ज्ञात कीजिये
View SolutionA(1,1) और B(−2,3) दो स्थिर बिंदु है एक बिंदु P इस प्रकार गति करता है की त्रिभुज PAB का क्षेत्रफल 9 वर्ग इकाई है , तो P के बिन्दुपथ का समीकरण ज्ञात कीजिए।
View Solutionयदि अक्षो को 45∘ से घुमाया जाये तो बिंदु (4,3) के नए निर्देशांक ज्ञात कीजिए ।
View Solutionएक सरल रेखा द्वारा अक्षो के बीच काटे गये अन्तः खण्ड को बिंदु (7,9),3:1 के अनुपात में अन्तः विभाजित करता है रेखा का समीकरण ज्ञात कीजिए
View Solutionरेखा 3x+2y=6 अक्षो को बिन्दुओ A और B पर काटती है ।बिंदु P इस प्रकार गति करता है की त्रिभुज PAB का क्षेत्रफल10 वर्ग इकाई रहता है , तो P का बिन्दुपथ ज्ञात कीजिए ।
View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए जो बिंदु (−1,5) से होकर जाती है ओर यह बिंदु उसके द्वारा 3:2 अक्षो के बीच कटे हुए भाग को 3:2 के अनुपात में विभाजित करता है
View Solutionएक सरल रेखा , अक्षो के साथ ऐसा समकोण त्रिभुज बनातीं है कि जिसके कर्ण कि लम्बाई √53 तथा क्षेत्रफल 7 वर्ग इकाई है । रेखा का समीकरण ज्ञात कीजिए
View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए जो बिंदु(1,2) से होकर जाती है जिसके द्वारा अक्षो से बने त्रिभुज का क्षेत्रफल 92 वर्ग इकाई है
View Solutionदो बिंदुओं P और Q के स्थिति सदिश क्रमशः 2¯a+¯b और ¯a−2¯b है। एक बिंदु R का स्थिति सदिश ज्ञात कीजिए जो रेखा खण्ड PQ को 1:2 के अनुपात में अंतः तथा बाहृातः विभाजित करता है।
View SolutionA और B दो बिंदु है। बिंदुओं A और B के स्थिति क्रमशः 6¯a−2¯b और ¯b−9¯a है। वह अनुपात ज्ञात कीजिए जिसमें बिंदु P जिसका स्थिति सदिश ¯a−¯b है रेखाखण्ड AB को विभाजित करता है।
View Solution
