निम्नलिखित सर्वसमिकाएँ सिद्ध कीजिए, जहाँ वे कोण, जिनके लिए व्यंजक परिभाषित है, न्यून कोण है :
सर्वसमिका cosec2A=1+cot2A को लागू करके
cosA−sinA+1cosA+sinA−1=cosecA+cotA
L.H.S=cosA−sinA+1cosA+sinA−1
=cotA−1+cosecAcotA+1−cosecA
(अंश और हर को sinA के भाग करने पर )
=(cotA+cosecA)−(1+cot2A)+cot2AcotA+1−cosecA
=(cotA+cossecA)−cosec2A+cot2AcotA+1−cosecA
(cotA+cosecA)−cosecA−cotA)
(cosecA+cotA)cotA+1−cosecA
=(cosecA+cotA)(1−cosecA+cotA)cotA+1−cosecA
=cosecA+cotA=R.H.S.
Topper's Solved these Questions
- त्रिकोणमिति का परिचय BOOK - NOOTAN HINDICHAPTER - त्रिकोणमिति का परिचय EXERCISE - विविध प्रश्नावली
38 Videos
- त्रिकोणमिति का परिचय BOOK - NOOTAN HINDICHAPTER - त्रिकोणमिति का परिचय EXERCISE - लघु उत्तरीय प्रश्न
34 Videos
- त्रिकोणमिति का परिचय BOOK - NOOTAN HINDICHAPTER - त्रिकोणमिति का परिचय EXERCISE - प्रश्नावली 8.3
11 Videos
- त्रिकोणमिति के कुछ अनुप्रयोग BOOK - NOOTAN HINDICHAPTER - त्रिकोणमिति के कुछ अनुप्रयोग EXERCISE - विविध प्रश्नावली (दीर्घ उतरिये प्रश्न)
6 Videos
Similar Questions
यदि tanθ=34, तो cosθ का मान ज्ञात कीजिए |
View Solutionसंलग्न चित्र में tan P - cos R का मान ज्ञात कीजिए |
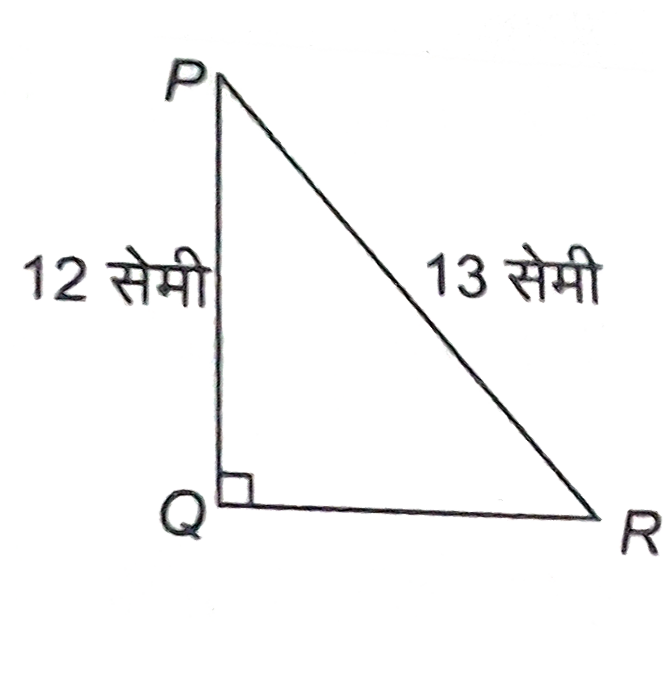
View Solutionsin18∘cos72∘ मान निकालिए :
View Solutionकिसी सीधी क्षैतिज सड़क के ऊपर एक हवाई जहाज क्रमागत किलोमीटर के दो पत्थरों के बीच उड़ रहा है। ये पत्थर हवाई जहाज के दोनों ओर स्थित हैं। हवाई जहाज से पत्थरों के अवनतांश 30∘ और 60∘ हैं। सड़क से वायुयान की ऊँचाई मीटर में ज्ञात कीजिए।
View Solution(cos A-sin A + 1) / (cos A + sin A-1) = csc A + cot A
View Solutionसर्वसमिका cosec2A=1+cot2A को लागू करके सिद्ध कीजिए कि
cosA−sinA+1cosA+sinA−1=cosecA+cotA
View SolutionProve that
(i)tanA+sinAtanA−sinA=secA+1secA−1
(ii)cotA−cosAcotA+cosA=cosecA−1cosecA+1
View Solutionसिद्ध करे की cotA+cosecA−1cotA−cosecA+1=1+cossinA
View Solutionसर्वसमिकाओ को सिद्ध करो:
cotA+cosecA−1cotA−cosecA+1=1+cosAsinA
View Solution(1+tan A)/(sin A)+(1+cot A)/(cos A)=2(sec A+cosec A)
View Solutionनिम्नलिखित सर्वसमिका सिद्ध कीजिए, जहाँ वे कोण, जिनके लिए व्यंजक परिभाषित है, न्यून कोण है :
cosA1+sinA+1+sinAcosA=2secA
View SolutioncosA−sinA+1cosA+sinA−1=cosecA+cotA
cosecA+cotA, = using the identity cosec2A=1+cot2A .
View Solution(cosecA−sinA)(secA−cosA)=1tanA+cotA
View SolutionsinA(cotA+3(3cotA+1)−1 cosec A−10cosA=
View SolutioncosA−sinA+1cosA+sinA−1=cosecA+cotA, using the identity cosec2A=1+cot
View SolutionProve that : (Using identify cosec2A=1+cot2A)
cosA−sinA+1cosA+sinA−1=cosecA+cotA.
View Solution
