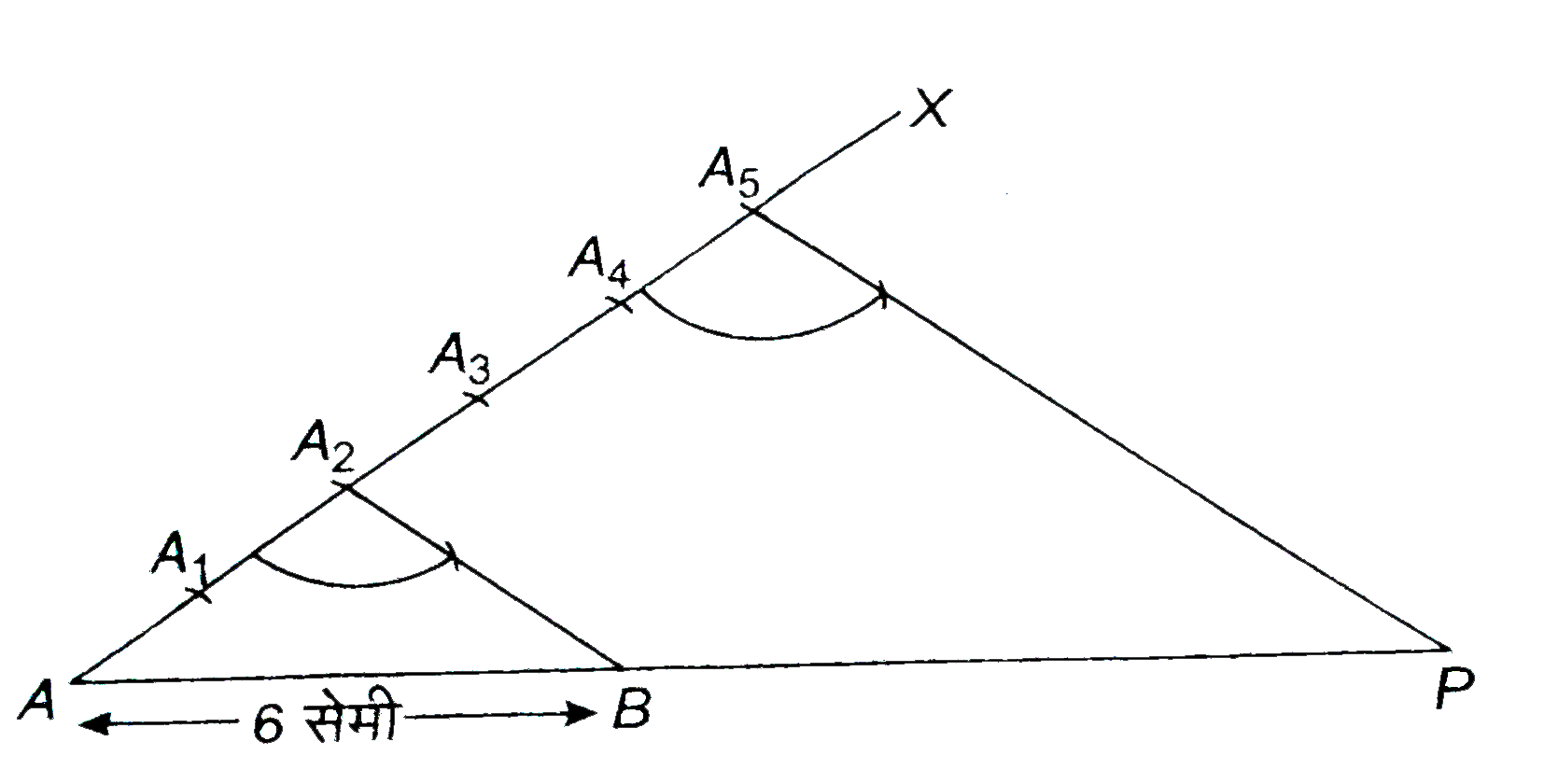
एक बिंदु ज्ञात कीजिए जो 6 सेमी लम्बे रेखाखण्ड को 3 : 5 के अनुपात में बाह्रातः विभाजित करता हैं ।
रचना के पद
1. रेखाखण्ड AB = 6 सेमी. खीचते हैं ।
2. AB से न्यूनकोण ∠ABX बनाती एक किरण खींचते हैं ।
3. BX पर बिंदु 5 बिंदु ( अनुपातों में बड़ा मान ) B1,B2,B3,B4,B5 इस प्रकार अंकित करते हैं कि
BB1=B1B2=B2B3=B3B4=B4,B5
4. B2(5−3) को अंतिम बिंदु A से मिलाया ।
5. B5सेB2A के समान्तर रेखा खींचते हैं जो बढ़ाई गई BA को P पर मिलाती हैं ।
इस प्रकार प्राप्त बिंदु P अभीष्ट बिंदु इस प्रकार है कि AP : BP = 3 : 5
औचित्यः △PBB5 में,
∵,B2A||B5P (रचना)
∴B2B5BB5=APBP (B.P.T से )
⇒35=APBP (रचना)
अतः रेखाखण्ड को 3 : 5 के अनुपात में बाह्रातः विभाजित करता हैं ।
Topper's Solved these Questions
- रचनाBOOK - NOOTAN HINDICHAPTER - रचनाEXERCISE - प्रश्नावली 11A
5 Videos
- रचनाBOOK - NOOTAN HINDICHAPTER - रचनाEXERCISE - प्रश्नावली 11B
7 Videos
- बहुपद BOOK - NOOTAN HINDICHAPTER - बहुपद EXERCISE - बहुविकल्पीय प्रश्न
7 Videos
- वास्तविक संख्याएँBOOK - NOOTAN HINDICHAPTER - वास्तविक संख्याएँEXERCISE - विविध प्रश्नावली
30 Videos
Similar Questions
10 सेमी लम्बाई के रेखाखण्ड को 5 : 4 के अनुपात में अंतः विभाजित कीजिए । रचना का औचित्य भी दीजिए ।
View Solution3.0 सेमी त्रिज्या का एक वृत्त खींचिए । इस पर एक बिंदु P लीजिए । बिंदु P से स्पर्श रेखा की रचना कीजिए ।
View Solutionयदि बहुपद 3x2+x−k का एक शून्यक 3 हैं, तो k का मान हैं
View Solutionयूक्लिड विभाजन प्रमेयिका बताइए।
View Solutionबिन्दुओ (4,0) और (0,12) को मिलाने वाली रेखा 3:1 को के अनुपात में ( i) आंतरिक और (ii ) बाह्य रूप में विभाजित करने वाले बिंदु के निर्देशांक ज्ञात कीजिये ।
View Solutionएक सरल रेखा द्वारा अक्षो के बीच काटे गये अन्तः खण्ड को बिंदु (7,9),3:1 के अनुपात में अन्तः विभाजित करता है रेखा का समीकरण ज्ञात कीजिए
View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए जो बिंदु (−1,5) से होकर जाती है ओर यह बिंदु उसके द्वारा 3:2 अक्षो के बीच कटे हुए भाग को 3:2 के अनुपात में विभाजित करता है
View Solutionएक त्रिभुज ABC में मध्यिकाएँ AD ,BE और CF एक बिंदु G से गुजरती है। यदि AD=9 सेमी ,GE=4.2 सेमी और GC=6 सेमी ,तो AG , BE औरFG की लम्बाइयों के मान ज्ञात कीजिए।
View Solutionदो बिंदुओं P और Q के स्थिति सदिश क्रमशः 2¯a+¯b और ¯a−2¯b है। एक बिंदु R का स्थिति सदिश ज्ञात कीजिए जो रेखा खण्ड PQ को 1:2 के अनुपात में अंतः तथा बाहृातः विभाजित करता है।
View SolutionA और B दो बिंदु हैं। बिंदु B का स्थिति सदिश ¯a+2¯b है। बिंदु P रेखा –खण्ड AB को 2:3 के अनुपात में विभाजित करता है। यदि बिंदु P का स्थिति सदिश 4¯a−¯b हो तो बिंदु A का स्थिति सदिश ज्ञात कीजिए।
View SolutionA और B दो बिंदु है। बिंदुओं A और B के स्थिति क्रमशः 6¯a−2¯b और ¯b−9¯a है। वह अनुपात ज्ञात कीजिए जिसमें बिंदु P जिसका स्थिति सदिश ¯a−¯b है रेखाखण्ड AB को विभाजित करता है।
View Solutionउस बिंदु का स्थिति सदिश ज्ञात कीजिए जो बिंदुओं जिनके स्थिति सदिश ¯a+3¯b और ¯a−¯b हैं को मिलाने वाले रेखा-खण्ड को 1:3 के अनुपात में विभाजित करता है।
View Solutionयदि बिंदु A जिसका स्थिति सदिश ¯a+2¯b है तथा सदिश ¯a,AB को 2:3 के अनुपात में विभाजित करता है तो B का स्थिति सदिश है:
View SolutionL लम्बाई की एक छड़ जिसके सिरे दो परस्पर लम्ब रेखाओं पर स्थित है , फिसलती है । छड़ को 1:2 के अनुपात में विभाजित करने वाले बिंदु का बिन्दुपथ ज्ञात कीजिए ।
View Solutionएक सरल रेखा बिन्दु (-1,5) से होकर जाती है और रेखा द्वारा अक्षो के बीच काटे हुए भाग को यह बिन्दु 3:2 के अनुपात में विभाजित करता है। रेखा का समीकरण ज्ञात कीजिए|
View Solutionमाना कि परवलय x2=8y का शीर्ष O तथा उस पर बिंदु Q है। यदि बिंदु P रेखाखण्ड OQ को 1:3 के आन्तरिक अनुपात में विभाजित करता है, तो P का बिन्दुपथ है :
View Solution
