आकृति में , छायांकित भाग का क्षेत्रफल ज्ञात कीजिए , जहाँ भुजा 12 सेमी वाले एक समबाहु त्रिभुज OAB के शीर्ष O को केंद्र मान कर 6 सेमी त्रिज्या वाला एक वृत्तीय चाप खींचा गया है ।
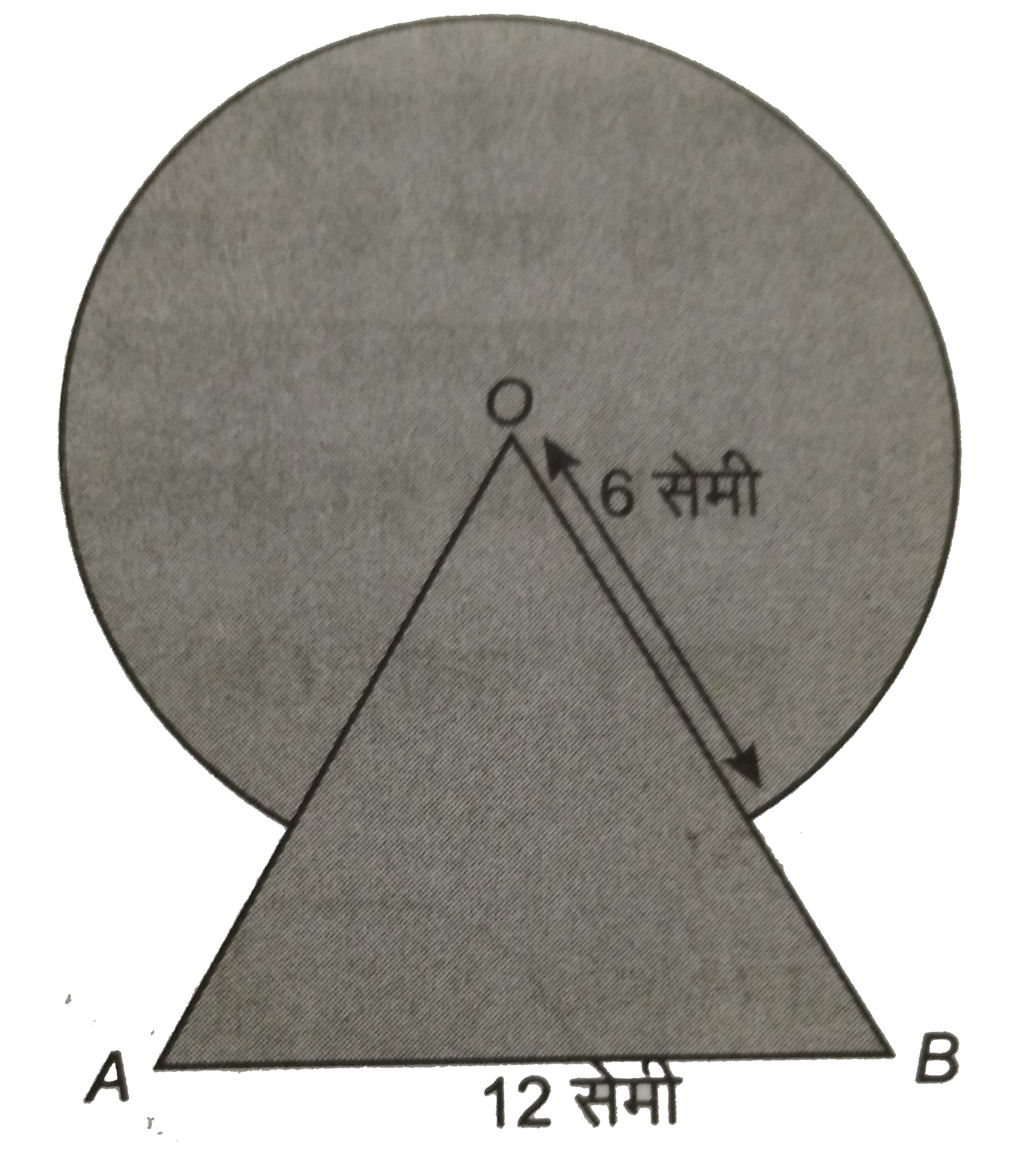
समबाहु त्रिभुज की प्रत्येक भुजा = 12 सेमी
तथा प्रत्येक कोण =60∘
अब , समबाहु त्रिभुज का क्षेत्रफल
=√34×( भुजा)2
=√34×12×12 सेमी2=36√3 सेमी2
वृत्त की त्रिज्या, r = 6 सेमी
दीर्घ त्रिज्यखण्ड का कोण , θ=360∘−60∘=300∘
∴ दीर्घ त्रिज्यखण्ड का क्षेत्रफल
=θ360∘×πr2
=300∘360∘×227×6×6=6607सेमी 2
अब , छायांकित भाग का क्षेत्रफल = समबाहु त्रिभुज का क्षेत्रफल + दीर्घ त्रिज्यखण्ड का क्षेत्रफल
=(36√3+6607) सेमी 2
Topper's Solved these Questions
- BOOK - NOOTAN HINDICHAPTER - वृत्तों से समबन्धित क्षेत्रफल EXERCISE - विविध प्रश्नावली ( अतिलघु उत्तरीय प्रश्न )24videos
वृत्तों से समबन्धित क्षेत्रफल
- BOOK - NOOTAN HINDICHAPTER - वृत्तों से समबन्धित क्षेत्रफल EXERCISE - विविध प्रश्नावली ( लघु उत्तरीय प्रश्न )24videos
वृत्तों से समबन्धित क्षेत्रफल
- BOOK - NOOTAN HINDICHAPTER - वृत्तों से समबन्धित क्षेत्रफल EXERCISE - प्रश्नावली 12.2 (एनo सीo ईo आरo टीo प्रश्न )28videos
वृत्तों से समबन्धित क्षेत्रफल
- BOOK - NOOTAN HINDICHAPTER - वृत्त EXERCISE - बहुविकल्पीय प्रश्न7videos
वृत्त
- BOOK - NOOTAN HINDICHAPTER - समान्तर श्रेढ़ी EXERCISE - विविध प्रश्नावली ( बहुविकल्पीय प्रश्न )7videos
समान्तर श्रेढ़ी
Similar Questions
एक वृत्त की त्रिज्या 7 सेमी है । इसका क्षेत्रफल ज्ञात कीजिए ।
06:07View Solutionदो वृत्त बाह्यतः स्पर्श करते है । इनके क्षेत्रफलों का योग 58π सेमी2 और इनके केन्द्रों के बीच की दूरी 10 सेमी है । दोनों वृत्तों की त्रिज्याएँ ज्ञात कीजिए ।
02:11View Solution6 सेमी त्रिज्या वाले एक वृत्त के एक त्रिज्याखंड का क्षेत्रफल ज्ञात कीजिए, जिसका कोण 60∘ है ।
01:31View Solutionयदि वृत्त की दो त्रिज्याओं के बीच का कोण 110∘ हो, तो इन त्रिज्याओं के सिरों पर खींची गई स्पर्श रेखाओं के बीच का कोण है :
02:45View Solution3 के प्रथम 6 गुणांकों का योग है:
02:17View SolutionWhich of the following are correct chain isomers of butane ? (i)
05:41View SolutionDetermine the point of symmetry of a regular hexagon.
02:10View SolutionDtermine the images of the following figure about the given line :
02:17View SolutionMatch the following Column A to Column B
 02:10View Solution
02:10View SolutionMatch the following Column A to Column B
 02:26View Solution
02:26View SolutionMatch the following Column A to Column B
 02:01View Solution
02:01View SolutionThe inequation represented by the graph given below is :
02:27View SolutionThe inequation that best describes the graph given below is _________
02:02View SolutionThe inequation that best describes the following graph is _________
02:54View Solutionएक समबाहु त्रिभुज की भुजाएँ 2 सेमी/से की दर से बढ़ रही है। क्षेत्रफल के बढ़ने की दर, जबकि भुजा 10 सेमी हो, है
01:27View Solutionकिसी वृत्त में एक चाप केन्द्र पर 45∘का कोण बनाता है। यदि चाप की लम्बाई 11 सेमी है तो वृत्त की त्रिज्या ज्ञात कीजिए।
01:54View Solution

