समद्विबाहु त्रिभुज ABC के आधार BC पर कोई बिन्दु D है। सिद्ध कीजिए कि AB>AD और AC>AD.
Da<aABC में,
AB=AC
⇒∠ACB=∠ABC ......(1)
ΔABD में,
∠ADC=∠ABD+∠BAD
(∠ADC बहिष्कोण है)
⇒∠ADC>∠ABD
impliesangleADCgtangleACD" "[समीकरण(1)से]<br>impliesACgtAD<br>पुनःDeltaACDमें,<br>angleADB=angleACD+angleCAD" "(angleADBबहिष्कोणहै)<br>impliesangleADBgtangleACD<br>impliesangleADBgtangleABD" "[समीकरण(1)से]<br>impliesABgtAD

Topper's Solved these Questions
- BOOK - NOOTAN HINDICHAPTER - त्रिभुज EXERCISE - प्रश्नावली 7A30videos
त्रिभुज
- BOOK - NOOTAN HINDICHAPTER - त्रिभुज EXERCISE - प्रश्नावली 7B19videos
त्रिभुज
- BOOK - NOOTAN HINDICHAPTER - त्रिभुज EXERCISE - विविधि प्रश्नावली ( दीर्घ उत्तरीय प्रश्न )8videos
त्रिभुज
- BOOK - NOOTAN HINDICHAPTER - चतुर्भुजEXERCISE - विविध प्रश्नावली24videos
चतुर्भुज
- BOOK - NOOTAN HINDICHAPTER - दो चरों वाले रैखिक समीकरण EXERCISE - विविध प्रश्नावली12videos
दो चरों वाले रैखिक समीकरण
Similar Questions
निम्नलिखित में से कौन-से त्रिभुजों के युग्म सर्वांगसम है ? प्रत्येक में सर्वागसमता का प्रतिबन्ध भी बताइए :
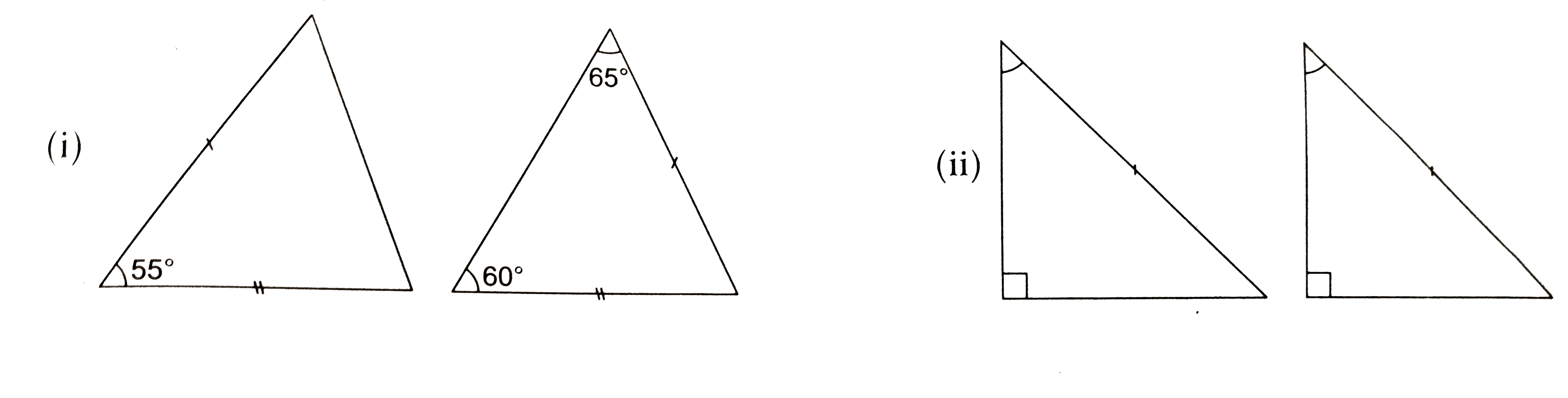
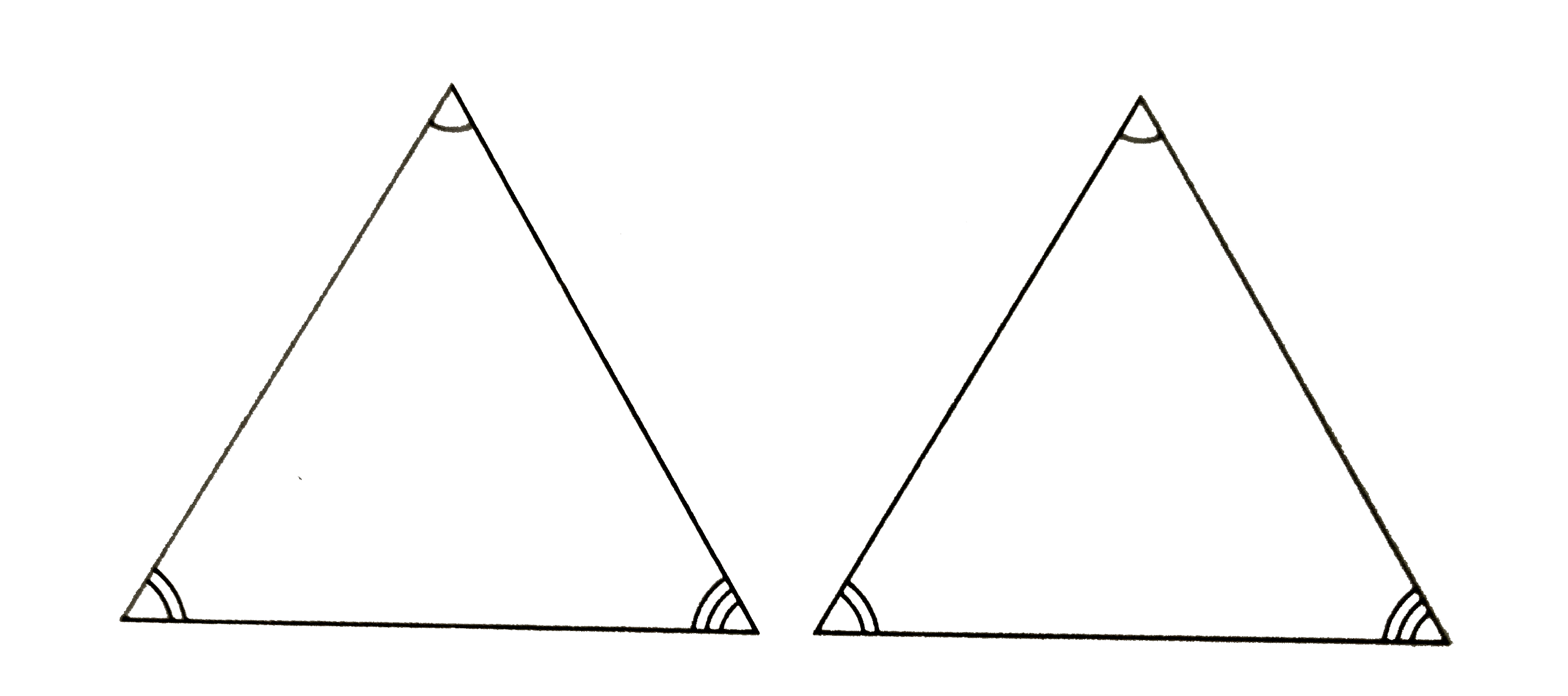
05:40View SolutionΔABC में, AB=8 सेमी, BC = 15 सेमी और AC = 17 सेमी है। सबसे कोण ज्ञात कीजिए।
03:54View Solutionदी आकृति में, यदि x = y और AB = CB है, तो सिद्ध कीजिए कि AE = CD है।
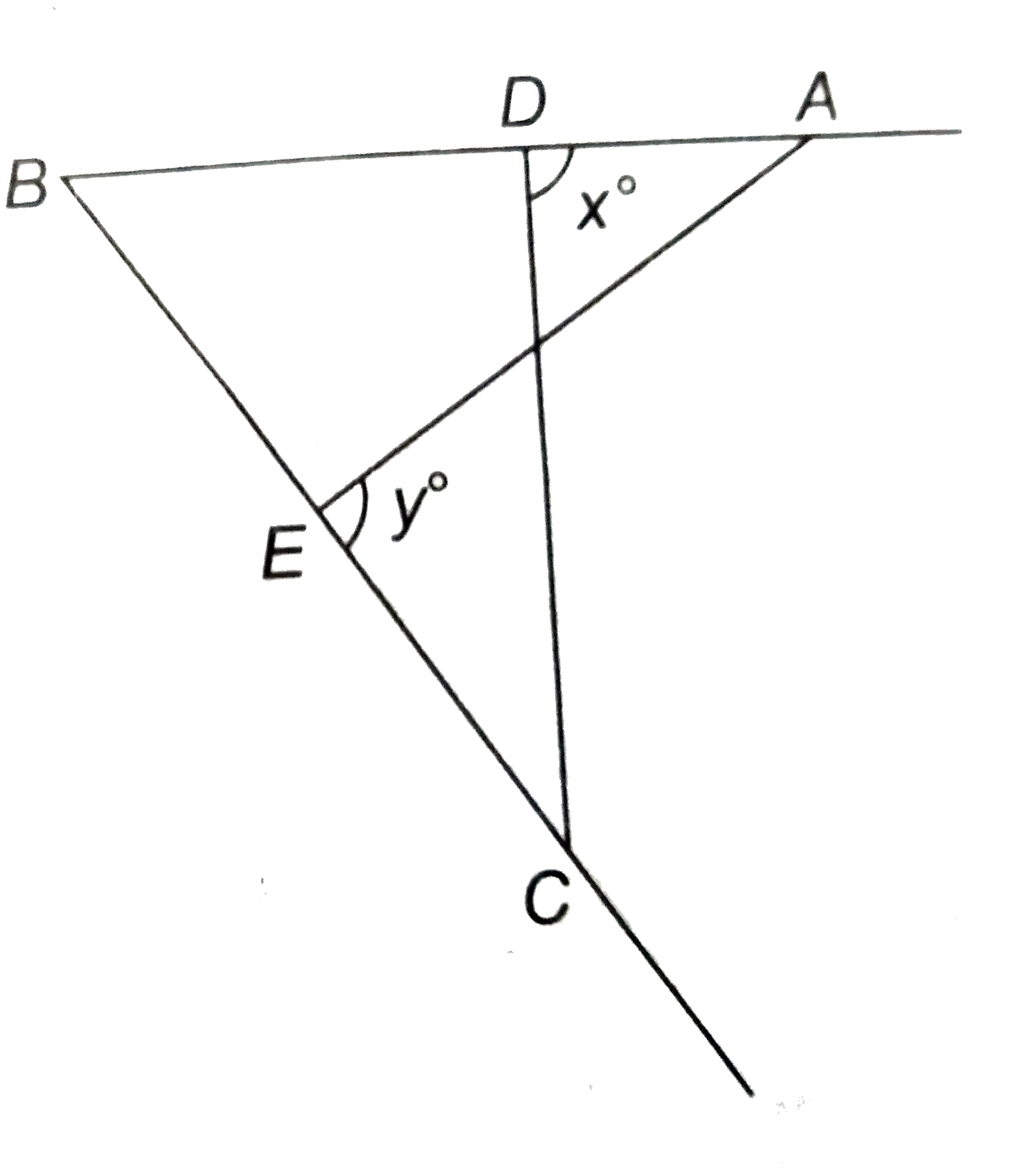 04:17View Solution
04:17View Solutionएक चतुर्भुज के तीन कोण 100∘,98∘,92∘ है। चौथा कोण ज्ञात कीजिए।
03:33View Solutionx अक्ष का समीकरण लिखिय|
06:40View Solutionसिद्ध कीजिए कि ΔABC एक समद्विबाहु त्रिभुज है यदि
∣∣ ∣ ∣∣1111+cosA1+cosB1+cosCcos2A+cosAcos2B+cosBcos2C+cosC∣∣ ∣ ∣∣=046:34View Solutionएक ही आधार BC पर तीन समद्विबाहु त्रिभुज △PBC ,△QBC और △RBC स्तिथ है। सिद्ध कीजिए कि P ,Q और R समरेख है।
04:14View Solutionसदिश विधि से सिद्ध करें कि यदि किसी त्रिभुज दो मध्यिकाएँ बराबर हों, तो त्रिभुज समद्विबाहु होता है |
06:21View Solutionसिद्ध कीजिए कि सम्मिश्र संख्याओं 0, 2i और √3+i को निरूपित करने वाले बिंदु समबाहु त्रिभुज के शीर्ष है।
03:33View Solutionसिद्ध कीजिए कि बिन्दु (2,−2),(8,4),(5,7) और (−1,1) एक आयत के शीर्ष है। उसके विकर्णों के बीच का न्यून कोण ज्ञात कीजिए।
03:53View Solutionत्रिभुज के आधार पर कुछ महत्वपूर्ण प्रश्न
04:09View Solutionसिद्ध कीजिए कि एक पासो के जोड़े को फेंकने पर पहले पर 5 आना , दूसरे पास पर 6 आने कि स्वतन्त्र घटनाएँ है।
02:40View Solutionयदि A, B, C, D समष्टि (space) में चार बिन्दु हैं, तो सिद्ध कीजिए कि |AB×CD+BC×AD+CA×BD|=4 ( त्रिभुज ABC का क्षेत्रफल )
View Solutionदिखाइए कि निम्नलिखित बिंदुओं के समूह एक समद्विबाहु त्रिभुज के शीर्ष हैं :
(0,5), (6,3) और (5,10)04:29View Solutionदिखाइए कि निम्नलिखित बिंदुओं के समूह एक समद्विबाहु त्रिभुज के शीर्ष हैं :
(1,1), (-1,-1) और (−√3,√3)04:12View Solution

