दर्शाइए कि एक रेखा पर एक दिए हुए बिन्दु से, जो उस रेखा पर स्थित नहीं है, जितने रेखाखण्ड खींचे जा सकते है उनमे लम्ब रेखाखण्ड सबसे छोटा होता है।
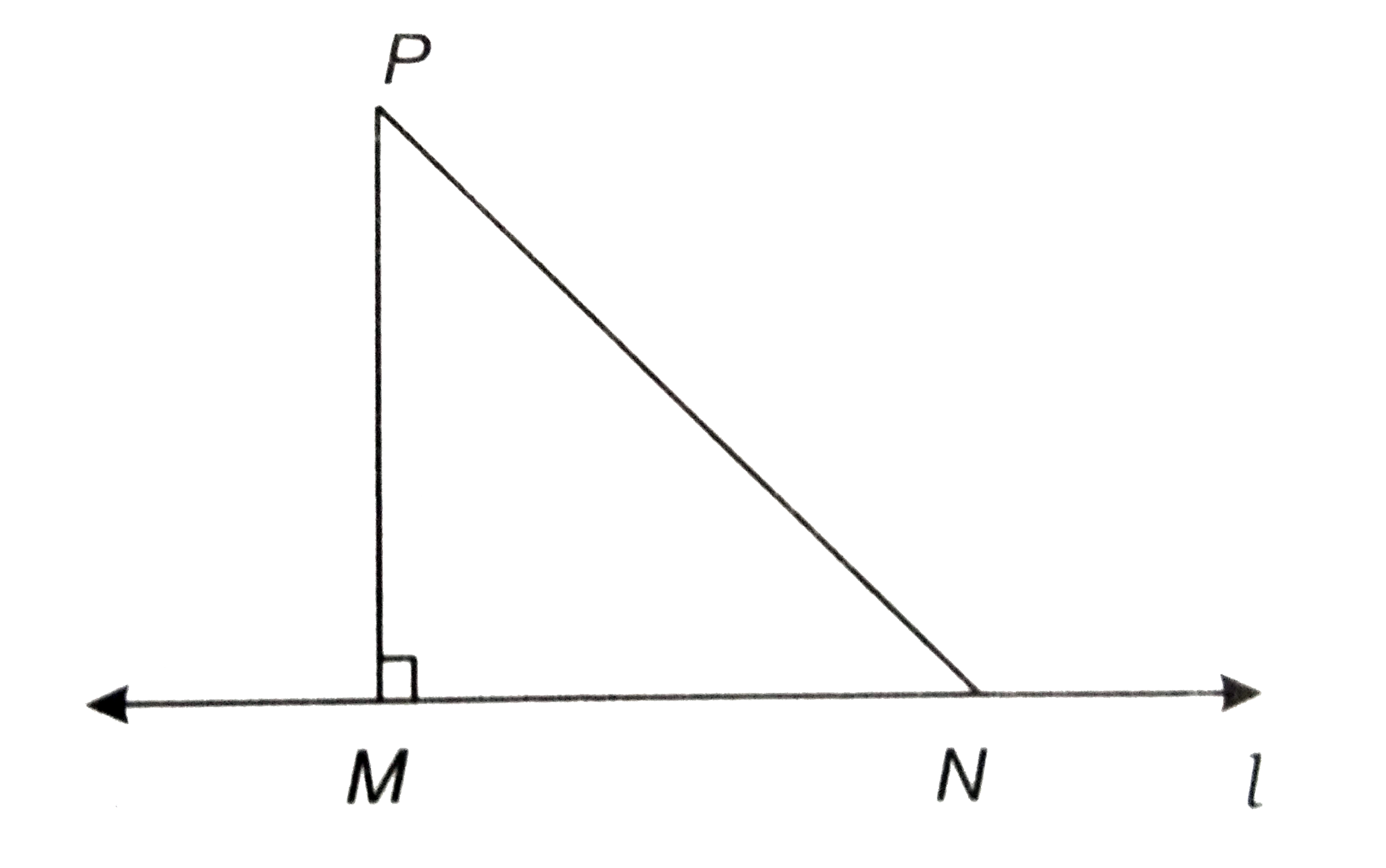
ज्ञात है : एक रेखा 'l' तथा इसके बाहर एक बिन्दु P है। P से रेखा 'l' पर लम्ब PM है। 'l' पर एक बिन्दु N है।
दर्शाना है : PM<PN
उपपत्ति : ΔPMN में,
∴∠PMN=90∘
⇒∠PNM न्यूनकोण होगा।
∴∠PNM<PMN⇒PM<PN
(कोण के समाने की भुजा )
Topper's Solved these Questions
- त्रिभुज Book:NOOTAN HINDIChapter:त्रिभुज Exercise:प्रश्नावली 7.5 ( ऐच्छिक)
Explore 4 Videos
- त्रिभुज Book:NOOTAN HINDIChapter:त्रिभुज Exercise:विविधि प्रश्नावली ( अतिलघु उत्तरीय प्रश्न )
Explore 10 Videos
- त्रिभुज Book:NOOTAN HINDIChapter:त्रिभुज Exercise:प्रश्नावली 7.3
Explore 5 Videos
- चतुर्भुजBook:NOOTAN HINDIChapter:चतुर्भुजExercise:विविध प्रश्नावली
Explore 24 Videos
- दो चरों वाले रैखिक समीकरण Book:NOOTAN HINDIChapter:दो चरों वाले रैखिक समीकरण Exercise:विविध प्रश्नावली
Explore 12 Videos
Similar Questions
ABC एक त्रिभुज है। इसके अभ्यन्तर में एक ऐसा बिन्दु ज्ञात कीजिए जो ΔABC के तीनो शीर्षो से समदूरस्थ है।
View Solutionएक समद्विबाहु ΔABC में, यदि ∠A=90∘ और AB = AC तो ∠B और ∠C ज्ञात कीजिए।
View SolutionΔABC और ΔDBC एक ही आधार BC पर बने दो समद्विबाहु त्रिभुज इस प्रकार है कि A और D भुजा BC के एक ही ओर स्थित है (देखिए आकृति)। यदि AD बढ़ाने पर BC को P पर प्रतिच्छेद करे, तो दर्शाइए कि :
(i) ΔABD≅ΔACD
(ii) ΔABP≅ΔACP
(iii) AP, कोण A और कोण D दोनों को समद्विभाजित करता है।
(iv) AP रेखाखण्ड BC का लम्ब समद्विभाजक है।

View Solutionएक चतुर्भुज के तीन कोण 100∘,98∘,92∘ है। चौथा कोण ज्ञात कीजिए।
View Solutionx अक्ष का समीकरण लिखिय|
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View Solutionपरवलय y2=4ax की नाभि तथा उस पर स्थित चर को मिलाने वाले रेखाखण्ड के मध्य - बिंदु का पथ एक परवलय है जिसकी नियता है :
View Solutionबिन्दु (1,0,0) से जाने वाली उस रेखा का समीकरण ज्ञात कीजिए जो XZ-समतल पर लम्ब है।
View Solutionएक रेखा के कार्तीय समीकरण 6x−2=3y+1=2z−2 है। रेखा के दिक्-अनुपात ज्ञात कीजिए तथा बिन्दु (2,−1,−1) से गुजरने वाली उस रेखा का सदिश समीकरण लिखिए जो दी हुई रेखा के समान्तर है।
View Solutionउस समतल का सदिश समीकरण जो बिन्दु A(4,7,−4) से जाता है तथा सदिश (3,2,−1)पर लम्ब है -
View Solution
