यदि चतुर्भुज ABCD में AB∣∣CD और AD=BC है तो सिद्ध कीजिए कि ∠A=∠B
बिंदु C से AD के समांतर रेखा CE खींचते हैं जो AB को बढ़ाने पर E पर मिलती है।
अब AB∣∣DC
⇒AE∣∣DC
□AECD में
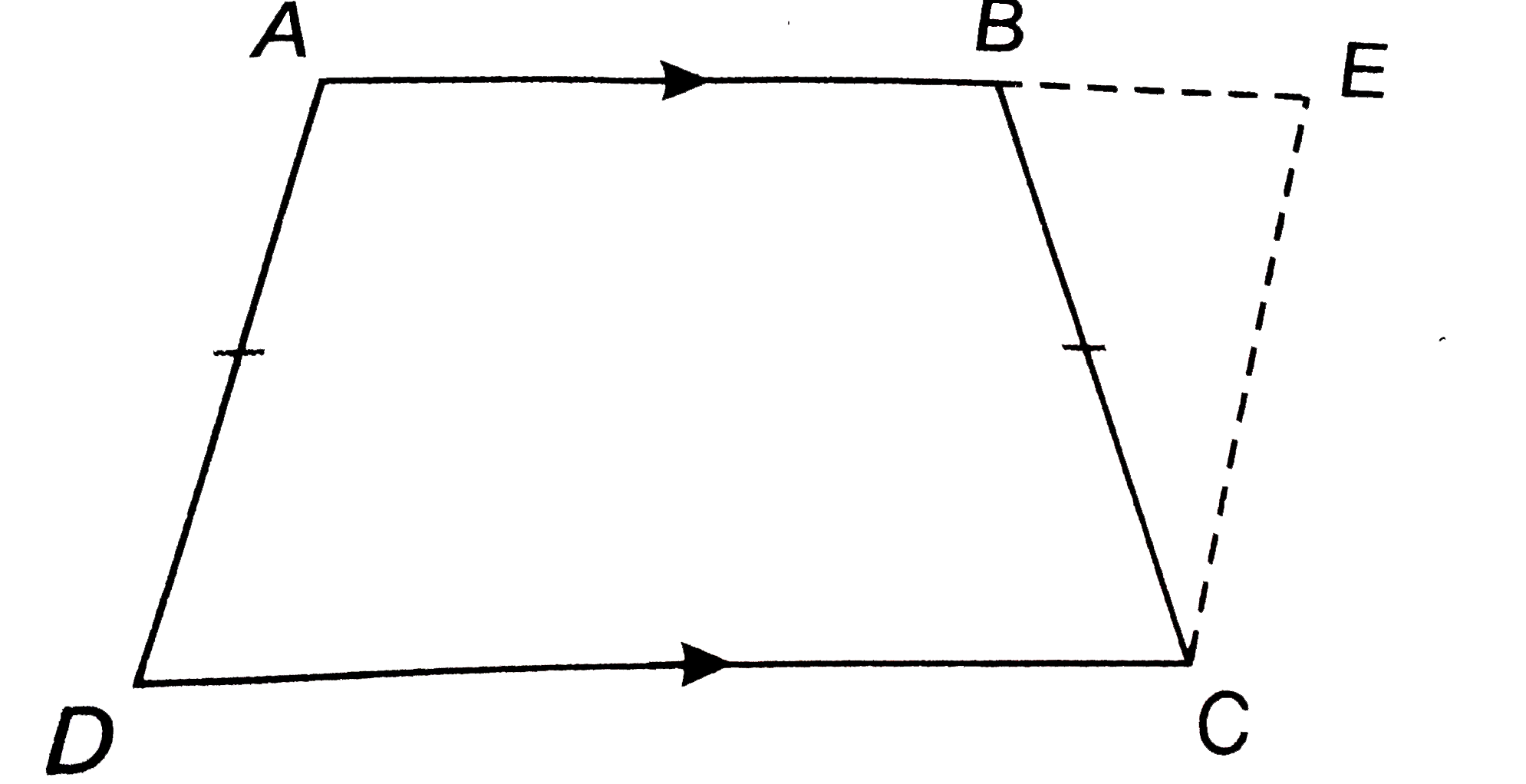
AE∣∣DC और AD∣∣EC
∴□AECD एक समांतर चतुर्भुज है।
⇒AD=CE
और ∠A+∠E=180∘
परंतु AD=BC (दिया है)
∴BC=CE
⇒∠BEC=∠CBE
⇒∠AEC=180∘−∠ABC
⇒∠E=180∘−∠B
⇒∠B=180∘−∠E
⇒∠B=∠A
Topper's Solved these Questions
- चतुर्भुजBOOK - NOOTAN HINDICHAPTER - चतुर्भुजEXERCISE - प्रश्नावली 8A
27 Videos
- चतुर्भुजBOOK - NOOTAN HINDICHAPTER - चतुर्भुजEXERCISE - प्रश्नावली 8B
15 Videos
- समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - NOOTAN HINDICHAPTER - समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - दीर्घ उत्तरीय प्रश्न
5 Videos
- त्रिभुज BOOK - NOOTAN HINDICHAPTER - त्रिभुज EXERCISE - विविधि प्रश्नावली ( दीर्घ उत्तरीय प्रश्न )
8 Videos
Similar Questions
एक चतुर्भुज के दो कोणों 89∘ और 113∘ है। यदि अन्य दो कोण बराबर है तो बराबर कोणों को ज्ञात कीजिए।
View Solutionएक समद्विबाहु त्रिभुज ABC की भुजाएं AB और AC बराबर है। D,E और F क्रमशः भुजाओं BC,CA और AB के मध्य बिंदु हैं सिद्ध कीजिए कि-
(i) रेखाखण्ड AD, रेखाखण्ड EF पर लम्ब है।
(ii) रेखाखण्ड AD रेखाखण्ड EF को समद्विभाजित करता है।
View Solutionसंलग्न चित्र में, ΔABC में AB का मध्य-बिन्दु D है तथा BC पर कोई बिन्दु P है। यदि CQ || PD, AB को Q पर मिलती है, तो सिद्ध कीजिए कि ar(ΔBPQ)=12ar(ΔABC)
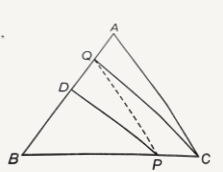
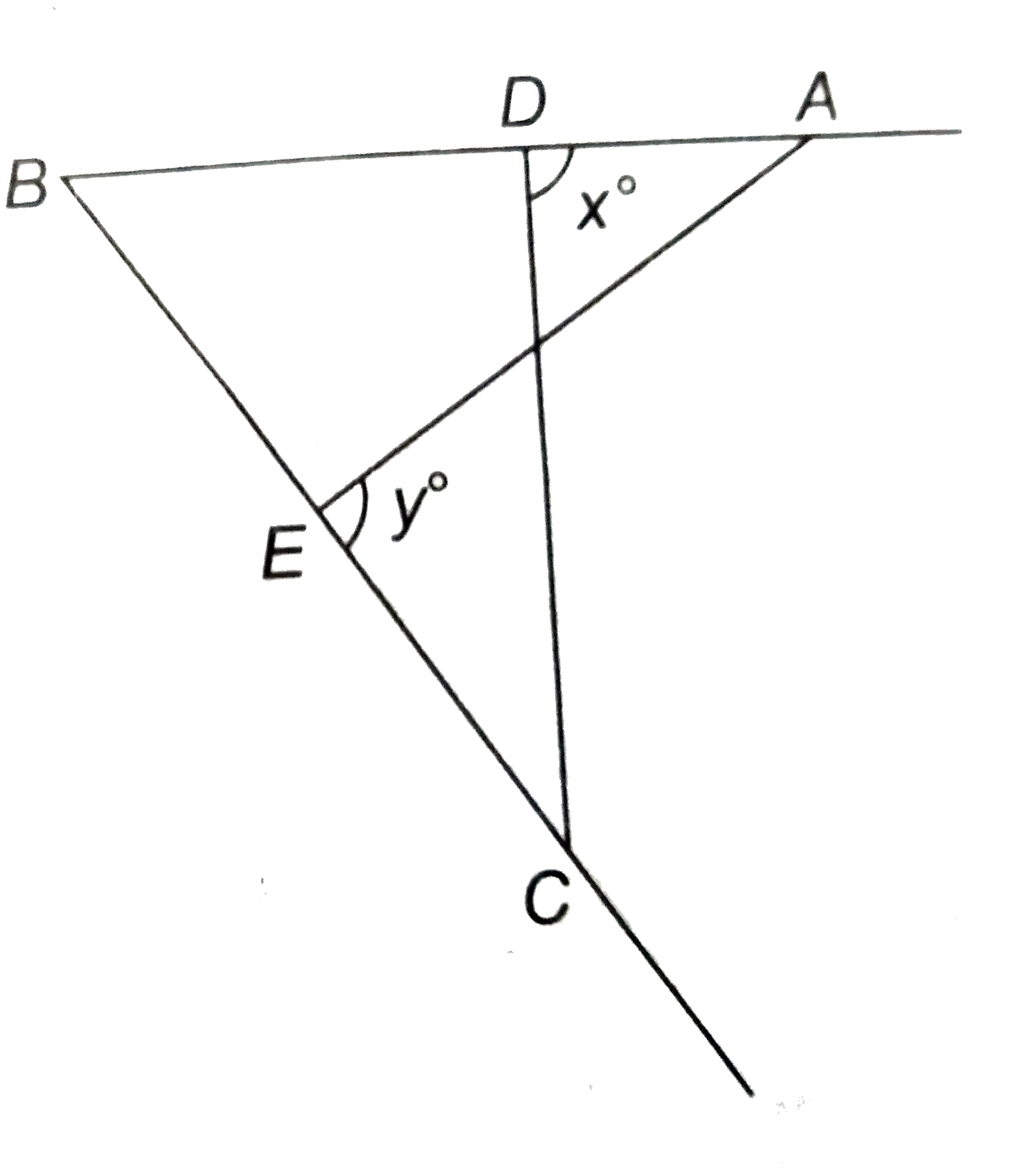
View Solutionदी आकृति में, यदि x = y और AB = CB है, तो सिद्ध कीजिए कि AE = CD है।
View SolutionIf ABCD is a quadrilateral in which ABCD and AD=BC, prove that ∠A =∠B.
View Solutionयदि किसी चतुर्भुज की भुजाओं को क्रमानुसार दिशा व परिमाण में निरूपित करने वाले सदिश ¯a,¯b,¯c,¯d हों तों सिद्ध कीजिए कि चतुर्भुज एक समांतर चतुर्भुज होगा यदि और केवल यदि ¯a+¯c=¯0 जिससे ¯b+¯d=¯0
View Solutionकिसी समांतर चतुर्भुज ABCD में यदि −−→AB=¯a तथा −−→BC=¯b तो सिद्ध कीजिए कि
−−→AC=¯a+¯b और −−→BD=¯b−¯a.
View Solutionयदि a,b,c,d गुणोत्तर श्रेढी में हों, तो सिद्ध कीजिए कि :
(b+c)(b+d)=(c+a)(c+d)
View Solutionयदि बिन्दु (a,b),(a',b') और (a−a',b−b') संरेख हो तो सिद्ध कीजिए कि
ab'=a'b.
साथ ही यह भी सिद्ध कीजिए कि इन बिन्दुओं से होकर जाने वाली रेखा मुलबिन्दु से होकर जाती है।
View Solutionयदि f:R→R इस प्रकार है कि f(x) = |x|, तो सिद्ध कीजिए कि fof = f .
View Solutionयदि →a×→b=→c×→bतो सिद्ध कीजिए →a−→c=λ→b कि जहाँ एक λ अदिश है।
View Solutionयदि ∣∣→a+→b∣∣=∣∣→b∣∣, तो सिद्ध कीजिए कि →a और →a+2→b परस्पर लम्ब है।
View Solutionबिंदु A(-3,-2), B(-6,a), C(-3,-4) और D(0,-1) चतुर्भुज ABCD के शीर्ष हैं , a ज्ञात कीजिए यदि 'a' ऋणात्मक और AB=CD हो।
View Solutionयदि x=asinθ और y=bcosθ हो, तो सिद्ध कीजिए कि
x2a2+y2b2=1
View Solutionयदि a:b=c:d हो, तो सिद्ध कीजिए कि
a2+ab+b2c2+cd+d2=a2−ab+b2c2−cd+d2
View Solution
