संलग्न चित्र में PQRS एक समांतर चतुर्भुज हैं A और B क्रमशः PQ और SR के मध्य बिंदु है। यदि PS=BR, तो सिद्ध कीजिए कि चतुर्भुज ADBC एक आयत है।

∵□PQRS एक समांतर चतुर्भुज है।
∴PQ=SR और PS=RQ
⇒12PQ=12SR
⇒PA=SB और AQ=BR……………..1 ( ∵ A और B मध्य बिंदु है)
अब PS=BR=SB=PA………….2
∵PQ∣∣SR
⇒PA∣∣SB………….3
∴ समीकरण 1 और 2 से
□PABS एक समांतर चतुर्भुज है।
लेकिन PA=PS=SB
∴□PABS एक समचतुर्भुज है।
इसी प्रकार □AQRB एक समचतुर्भुज है।
∴{∠1=90∘∠2=90∘ ( ∵ समचतुर्भुज के विकर्ण एक दूसरे के लम्ब समद्विभाजक है)
अब हम जानते हैं कि विकर्ण PB,∠P को तथा QB,∠Q को समद्विभाजित करता है।
लेकिन (∠3+∠4)+(∠5+∠6)=180∘ (एकान्तर अन्तः कोणों का योग)
⇒2∠4+2∠5=180∘
⇒∠4+∠5=90∘
=∠7=90∘
अब ABCD में ∠1=∠2=∠7=90∘
चतुर्भुज ABCD के चारों में प्रत्येक कोण 90∘ है।
अतः □ADB एक आयत है।

Topper's Solved these Questions
- चतुर्भुजBOOK - NOOTAN HINDICHAPTER - चतुर्भुजEXERCISE - प्रश्नावली 8A
27 Videos
- चतुर्भुजBOOK - NOOTAN HINDICHAPTER - चतुर्भुजEXERCISE - प्रश्नावली 8B
15 Videos
- समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - NOOTAN HINDICHAPTER - समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - दीर्घ उत्तरीय प्रश्न
5 Videos
- त्रिभुज BOOK - NOOTAN HINDICHAPTER - त्रिभुज EXERCISE - विविधि प्रश्नावली ( दीर्घ उत्तरीय प्रश्न )
8 Videos
Similar Questions
एक चतुर्भुज के दो कोणों 89∘ और 113∘ है। यदि अन्य दो कोण बराबर है तो बराबर कोणों को ज्ञात कीजिए।
View Solutionएक समद्विबाहु त्रिभुज ABC की भुजाएं AB और AC बराबर है। D,E और F क्रमशः भुजाओं BC,CA और AB के मध्य बिंदु हैं सिद्ध कीजिए कि-
(i) रेखाखण्ड AD, रेखाखण्ड EF पर लम्ब है।
(ii) रेखाखण्ड AD रेखाखण्ड EF को समद्विभाजित करता है।
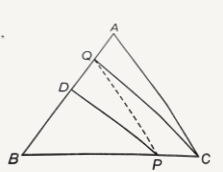
View Solutionसंलग्न चित्र में, ΔABC में AB का मध्य-बिन्दु D है तथा BC पर कोई बिन्दु P है। यदि CQ || PD, AB को Q पर मिलती है, तो सिद्ध कीजिए कि ar(ΔBPQ)=12ar(ΔABC)
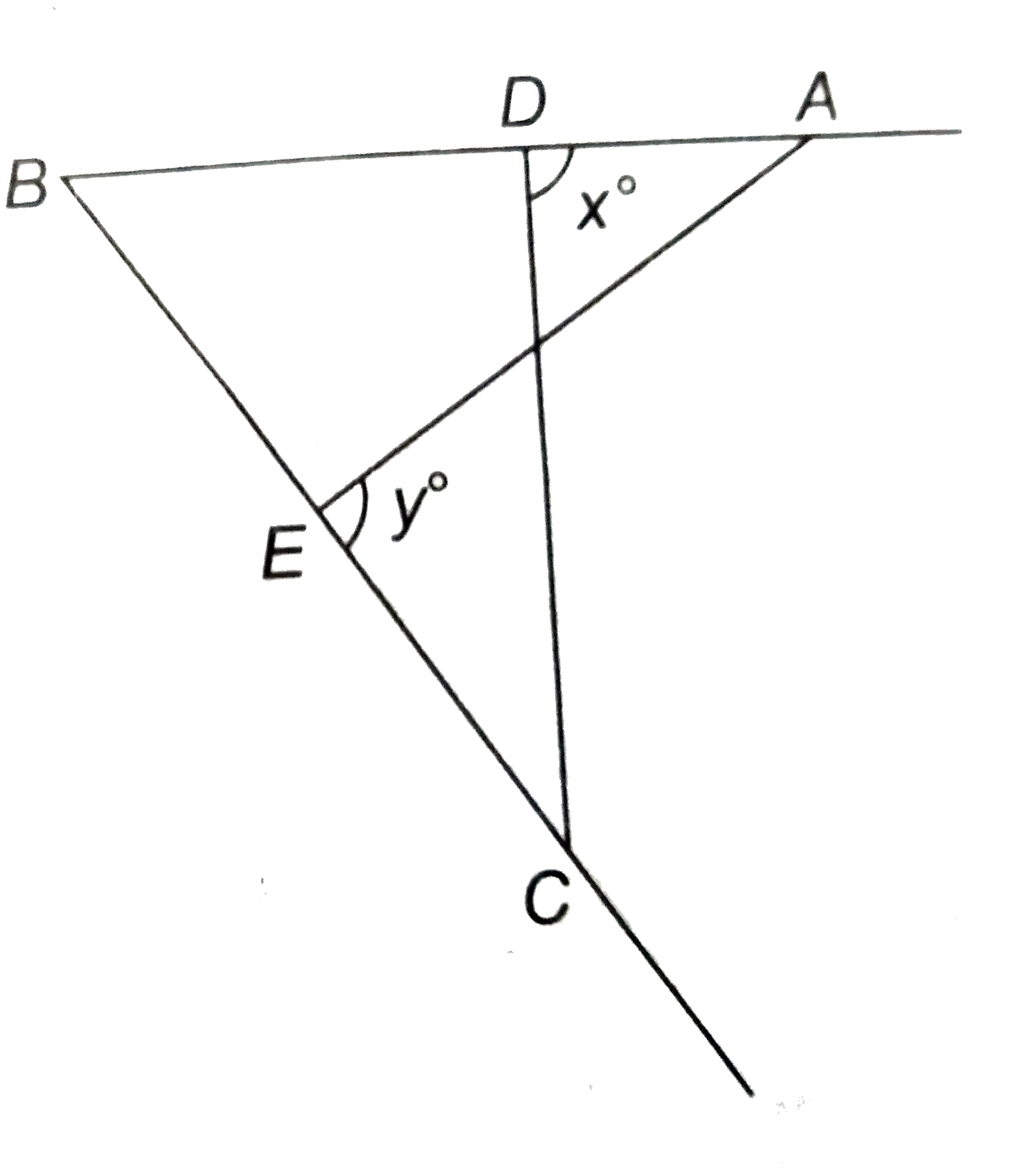
View Solutionदी आकृति में, यदि x = y और AB = CB है, तो सिद्ध कीजिए कि AE = CD है।
View SolutionWhich of the following are correct chain isomers of butane ? (i)
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionDtermine the images of the following figure about the given line :
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View SolutionIn the given figure, PQRS is a parallelogram. A and B are the mid-point of ¯¯¯¯¯¯PQ and ¯¯¯¯¯SR respectively. If PS=BR, then the quadrilateral ADBC is a…………………… ,
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C12_E05_020_Q01.png" width="80%"gt
View Solutionसिद्ध कीजिये की बिंदु (1,−2),(3,6),(5,10) और (3,2) एक समांतर चतुर्भुज के शीर्ष है ।
View Solutionयदि किसी चतुर्भुज की भुजाओं को क्रमानुसार दिशा व परिमाण में निरूपित करने वाले सदिश ¯a,¯b,¯c,¯d हों तों सिद्ध कीजिए कि चतुर्भुज एक समांतर चतुर्भुज होगा यदि और केवल यदि ¯a+¯c=¯0 जिससे ¯b+¯d=¯0
View Solution
