समान्तर चतुर्भुज ABCD में, X और Y क्रमशः भुजाओं BC और CD के मध्य-बिन्दु है। सिद्ध कीजिए कि ar(ΔAXY)=38ar(||gm ABCD)
BD, BY और AC को मिलाया।
∵ X, BC का मध्य-बिन्दु है।
∴YX,ΔCYB की माध्यिका है।
∴ar(ΔCYX)=12ar(ΔCYB) (∵ माध्यिका त्रिभुज को दो बराबर क्षेत्रफलों में विभाजित करती है)
=12×12ar(ΔDBC)=14ar(ΔDBC) (∵ माध्यिका को दो बराबर क्षेत्रफलों में विभाजित करती है)
=14×12ar(||gm ABCD)
(∵ विकर्ण DB, ||gm को दो बराबर भागो में विभाजित करता है)
=18ar(||gm ABCD) ...(1)
अब, ar(ΔABC)=12ar(||gm ABCD) (∵ विकर्ण DB, ||gm को दो बराबर भागो में विभाजित करता है)
2ar(ΔABX)=12ar(||gm ABCD) (∵ माध्यिका AX, ΔABC को दो बराबर भागो में विभाजित करता है)
⇒ar(ΔABX)=14ar(||gm ABCD) ...(2)
इसी प्रकार ⇒ar(ΔAYD)=14ar(||gm ABCD) ...(3)
अब समीकरण (1), (2) और (3) से
ar(ΔAXY)=ar(||gm ABCD)−[ar(ΔABX)+ar(ΔAYD)+ar(ΔCYX)]
=ar(||gm ABCD)−(14+14+18)ar(||gm ABCD)
=ar(||gm ABCD)[1−58]=38ar(||gm ABCD)

Topper's Solved these Questions
- समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - NOOTAN HINDICHAPTER - समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली
27 Videos
- समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - NOOTAN HINDICHAPTER - समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 9.1
1 Videos
- चतुर्भुजBOOK - NOOTAN HINDICHAPTER - चतुर्भुजEXERCISE - विविध प्रश्नावली
24 Videos
Similar Questions
एक समान्तर चतुर्भुज का आधार, संगत शीर्षलम्ब का 3 गुना है। यदि समान्तर चतुर्भुज का क्षेत्रफल 48 वर्ग सेमी है, तो समान्तर चतुर्भुज का आधार और संगत शीर्षफ़ल ज्ञात कीजिए।
View Solutionनिम्नलिखित आकृतियों में से कौन-सी आकृतियाँ एक ही आधार और एक ही समान्तर रेखाओं के बीच स्थित है? ऐसी स्थिति में, उभयनिष्ठ आधार और दोनों समान्तर रेखाएँ लिखिए।
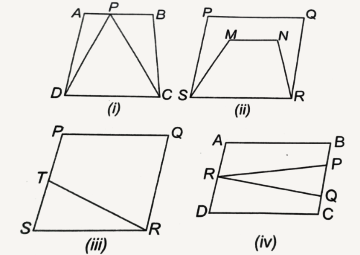
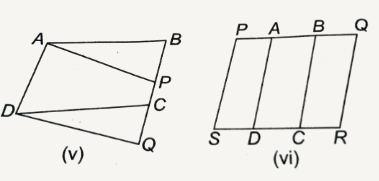
View Solutionएक चतुर्भुज के तीन कोण 100∘,98∘,92∘ है। चौथा कोण ज्ञात कीजिए।
View SolutionABCD is a parallelogram. X and Y are mid-points of BC and CD. Prove that ar(triangleAXY)=3/8ar(||^[gm] ABCD)
View SolutionIf ABCD is a parallelogram, the prove that ar(ABD)=ar(BCD)=ar(ABC)=ar(ACD)=1/2a r(∣∣gmA B C D)
View SolutionIn figure, CD∣∣AE and CY∣∣BA. Prove that ar(ΔCBX)=ar(ΔAXY).
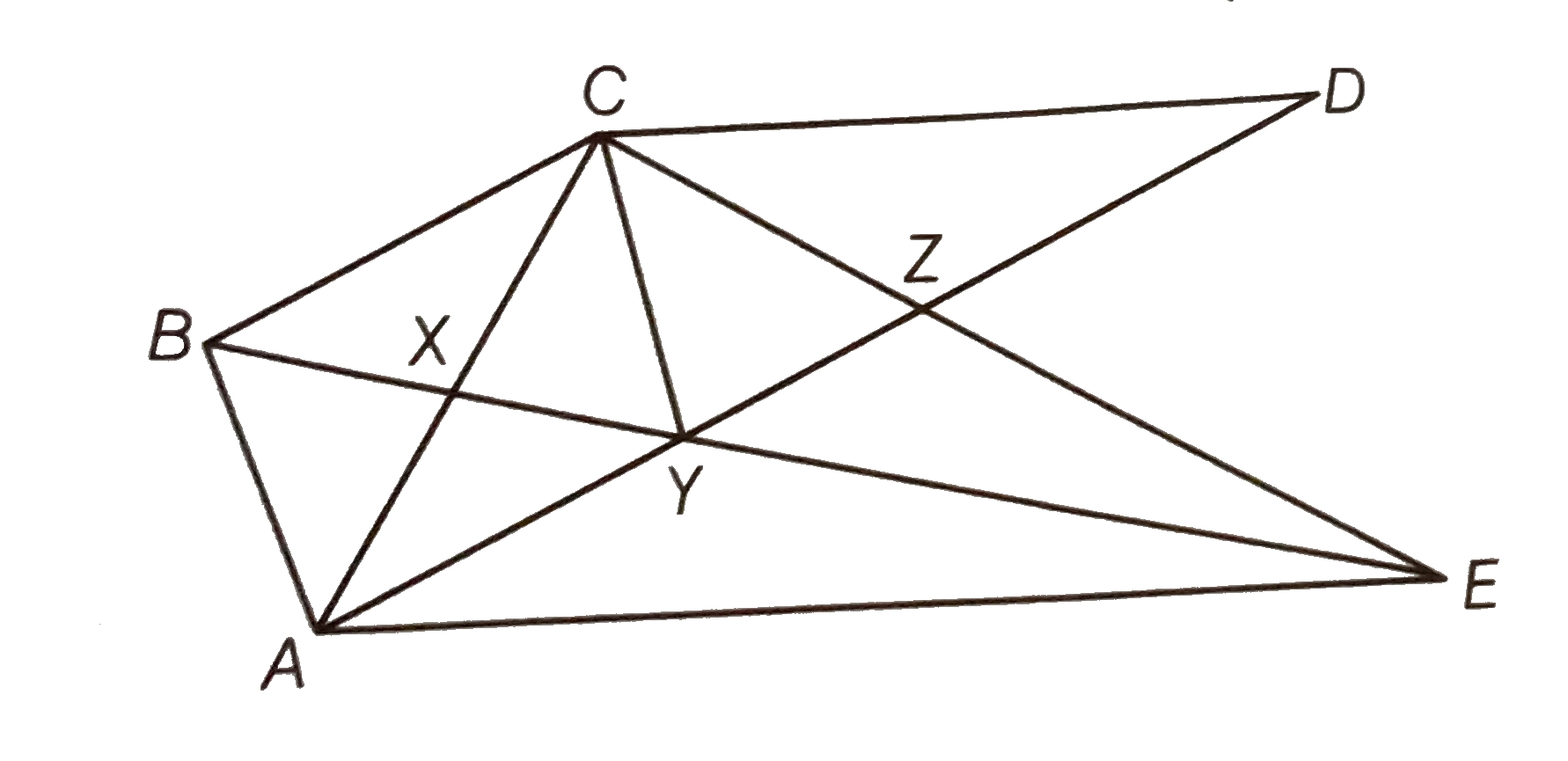
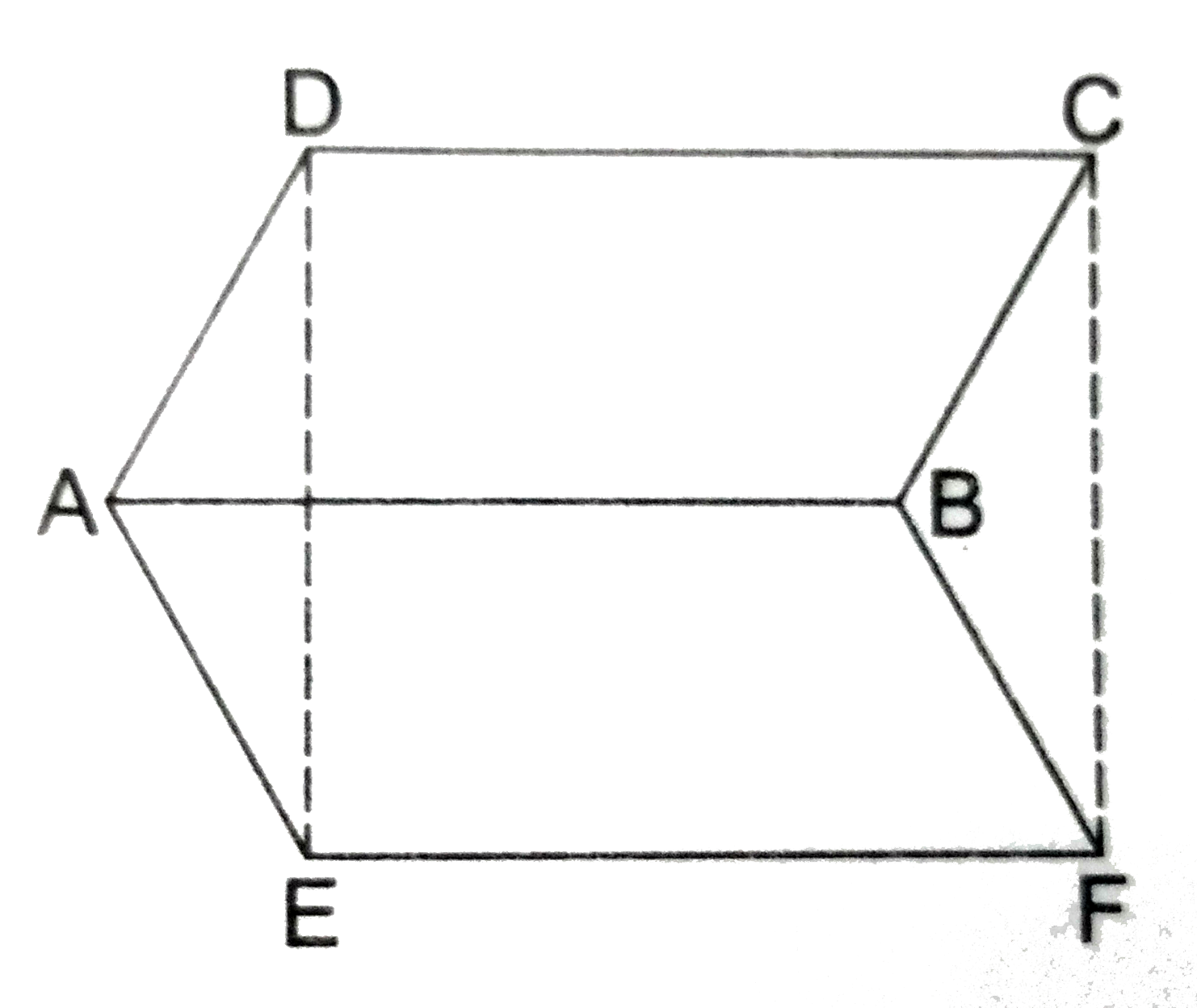
View SolutionIn the adjoing figure, two parallelograms ABCD and AEFB are drawn on opposite sides of AB. Prove that
ar(||gm ABCD)+ar(||gm AEFB)
=ar(||gm EFCD).
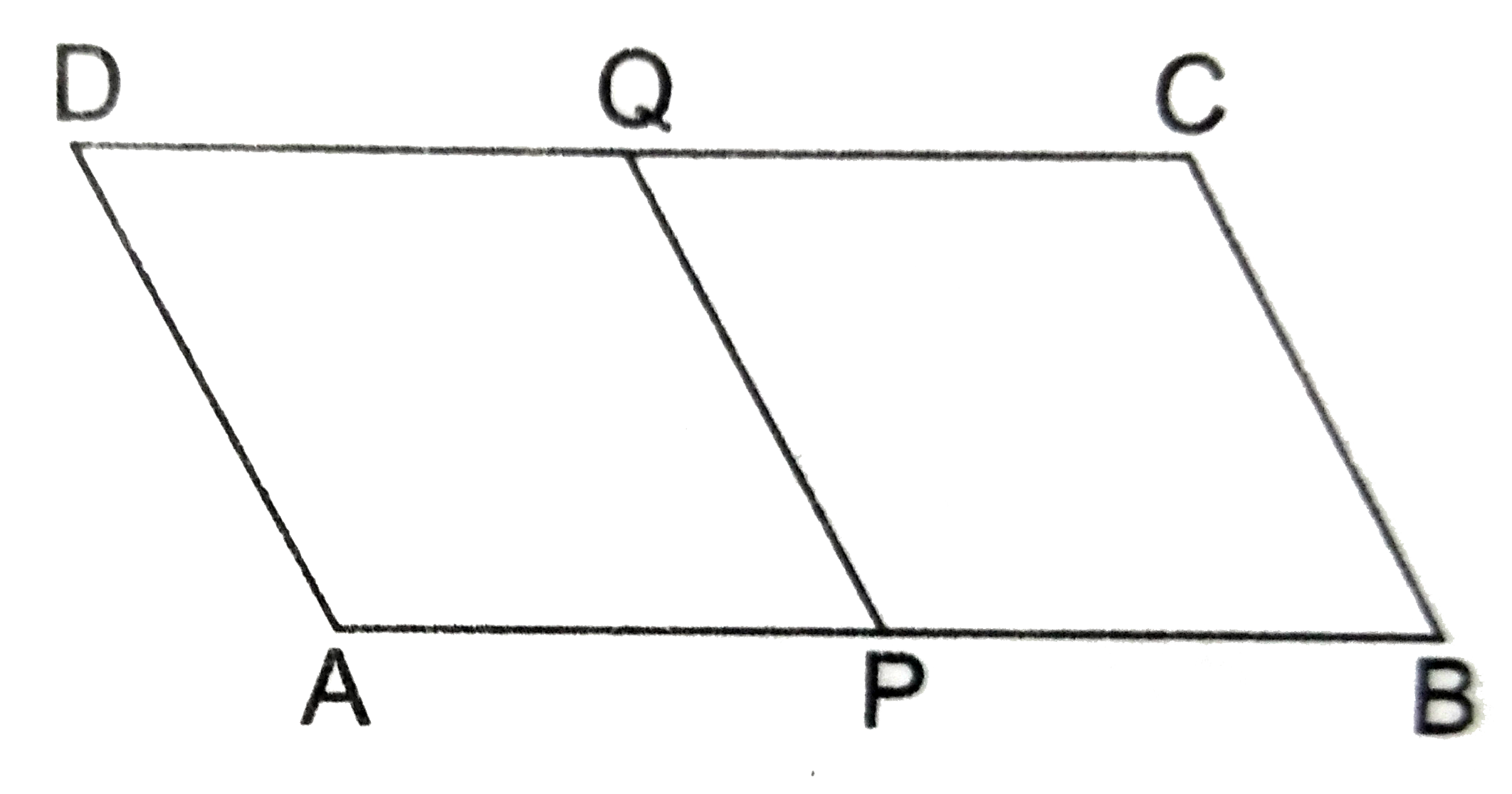
View SolutionIn a ∣∣gm ABCD, if P and Q are midpoints of AB and CD respectively and ar(||^(gm) ABCD) =16cm2 then ar (∣∣gm APQD) = ?
View SolutionABCD एक समांतर चतुर्भुज है भुजाओं BC तथा CD के मध्य-बिंदु क्रमशः X तथा Y है। सिद्ध कीजिए कि ar(ΔAXY)=38ar(।।gmABCD)
View Solutionयदि ABCD एक समांतर चतुर्भुज है, तो सिद्ध कीजिए कि
ar(ΔABD)=ar(ΔBCD)=ar(ΔABC)=ar(ΔACD)=12ar(||gmABCD)
View Solutionकिसी समांतर चतुर्भुज ABCD में यदि −−→AB=¯a तथा −−→BC=¯b तो सिद्ध कीजिए कि
−−→AC=¯a+¯b और −−→BD=¯b−¯a.
View Solutionसिद्ध कीजिए कि बिंदुओं (2,3) और(3,4) को मिलाने वाले रेखाखण्ड के मध्य बिंदु के निर्देशांक x और y निम्नलिखित समीकरण को संतुष्ट करते है :
x−y+1=0.
View Solutionसिद्ध कीजिए कि बिन्दु (2,−2),(8,4),(5,7) और (−1,1) एक आयत के शीर्ष है। उसके विकर्णों के बीच का न्यून कोण ज्ञात कीजिए।
View Solutionबिन्दु (1,1) पर वक्रों y=x2 और x=y2 के मध्य कोण है
View Solutionबिंदु A(-3,-2), B(-6,a), C(-3,-4) और D(0,-1) चतुर्भुज ABCD के शीर्ष हैं , a ज्ञात कीजिए यदि 'a' ऋणात्मक और AB=CD हो।
View Solution
