वास्तविक संख्याओं के समुच्चय R पर एक सम्बन्ध R1 इस प्रकार परिभाषित है कि-
(a,b)∈R1⇔1+ab>0 जबकि a,b∈R
सिद्ध कीजिए कि-
(i) प्रत्येक a∈R के लिये (a,a)∈R1
(ii) (a,b)∈R1⇒(b,a)∈R1 जबकि a,b∈R
(iii) (a,b)∈R1 और (b,c)∈R1⇒(a,c)∈R1 सत्य नहीं है जबकि a,b,c∈R
Step by step video & image solution for वास्तविक संख्याओं के समुच्चय R पर एक सम्बन्ध R_(1) इस प्रकार परिभाषित है कि- (a, b) in R_(1) hArr 1 + ab gt 0 जबकि a, b in R सिद्ध कीजिए कि- (i) प्रत्येक a in R के लिये (a, a) in R_(1) (ii) (a, b) in R_(1) rArr (b, a) in R_(1) जबकि a, b in R (iii) (a, b) in R_(1) और (b, c) in R_(1) rArr (a, c) in R_(1) सत्य नहीं है जबकि a, b, c in R by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- सम्बन्ध एवं फलनBOOK - NOOTAN HINDICHAPTER - सम्बन्ध एवं फलनEXERCISE - प्रश्नावली 2C
36 Videos
- सम्बन्ध एवं फलनBOOK - NOOTAN HINDICHAPTER - सम्बन्ध एवं फलनEXERCISE - प्रश्नावली 2D (निम्नलिखित फलनों के प्रान्त ज्ञात कीजिए -)
10 Videos
- सम्बन्ध एवं फलनBOOK - NOOTAN HINDICHAPTER - सम्बन्ध एवं फलनEXERCISE - प्रश्नावली 2A
20 Videos
- समुच्चयBOOK - NOOTAN HINDICHAPTER - समुच्चयEXERCISE - विविध प्रश्नावली
16 Videos
- सम्मिश्र संख्याएँ एवं द्विघात समीकरण BOOK - NOOTAN HINDICHAPTER - सम्मिश्र संख्याएँ एवं द्विघात समीकरण EXERCISE - प्रश्नावली 5F
10 Videos
Similar Questions
माना f⊆Z×Z निम्नवत परिभाषित है-
f{(ab,a+b):a,b∈Z}
क्या f, Z से Z में एक फलन है? अपने उत्तर का औचित्य भी बताइए ।
View Solution1x−3 का प्रान्त ज्ञात कीजिए ।
View Solutionयदि (x3+1,y−23)=(53,13), तो x और y के मान ज्ञात कीजिए ।
View Solutionनिम्नलिखित समुच्यों में से कौन किसका उपसमुच्चय है इसका निर्णय कीजिएः
A={x:xεR तथा x2−8x+12=0 को संतुष्ट करने वाली सभी वास्तविक संख्याएं x}
B={2,4,6},C={2,4,6,8,…},D=(6)
View Solutionयदि z−1z+1 एक शुद्ध काल्पनिक संख्या है, तो |z| का मान है-
View SolutionFor the relation R1 defined on R by the rule (a,b)∈R1:1+ab>0. Prove that: for(a,b)∈R1and(b,c)∈R1then(a,c)∈R1 is not true for all a,b,c∈R
View SolutionIn a triangle ABC,(r_(1)-r)/(a)+(r_(2)-r)/(b)+(r_(3)-r)/(c)=
View SolutionTwo resistors of resistances R_(1)=100 pm 3 ohm and R_(2)=200 pm 4 ohm are connected (a) in series, (b) in parallel. Find the equivalent resistance of the (a) series combination, (b) parallel combination. Use for (a) the relation R=R_(1)+R_(2) and for (b) 1/(R')=1/R_(1)+1/R_(2) and (Delta R')/R'^(2)=(Delta R_(1))/R_(1)^(2)+(Delta R_(2))/R_(2)^(2)
View SolutionA relation R1 is defined on the set of real numbers as follows:
(a,b)∈R1⇔1+ab>0, when a, b ∈ R
(iii) (a,b)∈R1and(b,c)∈R1→(a,c)∈R1 is not true when a , b, c, ∈R
View SolutionLet R1 be a relation defined by
R1={(a,b)∣a>b,a,b∈R}. Then R1 , is
View Solutionमाना कि R1=R−{−1} तथा R1 पर एक संक्रिया ∗,a∗b=a+b+ab∀a,b∈R1 द्वारा परिभाषित है। R1 में तत्समक अवयव तथा अवयवों के प्रतिलोम निकालें।
View Solutionवास्तविक संख्याओं के समुच्चय R में एक संबंध R1 इस प्रकार परिभाषित है कि (a,b)∈R1⇔1+ab>0 सभी a,b∈R के लिए। दर्शाइए कि R1 स्वतुल्य है और सममित है परन्तु संक्रामक नहीं है।
View SolutionProve the questions
a(rr1+r2r3)=b(rr2+r3r1)=c(rr3+r1r2)
View Solutionयदि द्विआधारी संक्रिया ∗ वास्तविक संख्याओं के समुच्चय R पर इस प्रकार परिभाषित है कि
a∗b=ab2+1, जहाँ a,b∈R
तो द्विआधारी संक्रिया ∗ के साहचर्यता (associativity) की जाँच कीजिए।
View SolutionA long cylindrical conductor of radius R carries I as shown. The current density is a function of radius r as j = br, where b is a constant. The magnetic field at a distance r1(r1<R) is
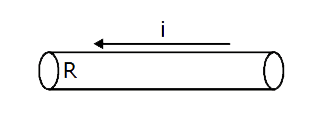
View Solution
