तीन संकेन्द्रीय धात्विक कोशों A, B और C की त्रिज्याएँ क्रमशः a, b और c(a<b<c) हैं, जिनके पृष्ठ आवेश घनत्व क्रमशः +σ,−σ और +σ हैं। तब कोश B पर विभव का मान होगा-
σε0(a2−b2a+c)
σε0(a2−b2b+c)
σε0(b2−c2b+a)
σε0(b2−c2c+a)
The correct Answer is:B
पर विभव A के कारण विभव +B के कारण द्विभाव +C के कारण विभव =14πε0[σ.4πa2b+−σ.4πb2b+σ.4πc2b]
खोखले चालक C के अंदर द्विभाव उसके पृष्ट के विभव के बराबर होगा
B पर विभव =σε0(a2b−b2b+c2c)
=σε0(a2−b2b+c)
Topper's Solved these Questions
- BOOK - NAVBODHCHAPTER - स्थिरवैद्युत विभव तथा धारिता EXERCISE - NCERT पाठयपुष्तक के प्रश्नोत्तर65videos
स्थिरवैद्युत विभव तथा धारिता
- BOOK - NAVBODHCHAPTER - स्थिरवैद्युत विभव तथा धारिता EXERCISE - बोधात्मक प्रश्न प्लस29videos
स्थिरवैद्युत विभव तथा धारिता
- BOOK - NAVBODHCHAPTER - स्थिर विद्युत विभव एवं धारिताEXERCISE - आंकिक प्रश्न12videos
स्थिर विद्युत विभव एवं धारिता
Similar Questions
5×10−8C तथा −3×10−8C के दो आवेश 16cm दुरी पर स्थित है दोनों आवेशों को मिलाने वाली रेखा के किस बिंदु पर विघुत विभव शून्य होगा? अनंत पर विभव शून्य लिखिय?
02:28View Solutionधातु की दो समरूप प्लेटों को q1 और q2 आवेश इस प्रकार दिये जाते हैं कि q2<q1 अब दोनों प्लेटें एक-दूसरे के समीप लायी जाती हैं ताकि दोनों प्लेटें धारिता C वाले समांतर प्लेट संधारित्र का निर्माण कर सके। प्लेटों के बीच विभवान्तर ज्ञात कीजिए।
04:38View Solutionक्या 1 सैमी त्रिज्या का धातु का गोला एक कूलाम आवेश धारण कर सकता है ?
02:15View Solutionयदि ω(≠1) इकाई का घनमूल है और (1+ω)7=A+Bω हो, तो A और B क्रमशः होंगे
03:32View Solutionमाना R3 में p, q और r तीन असमतलीय सदिश हैं। माना सदिश s के घटक क्रमागत सदिशों p, q एवंr के अनुदिश क्रमशः 4, 3 और 5 हैं। यदि s के घटक क्रमागत सदिशों (−p+q+r),(p−q+r) एवं (−p−q+r) के अनुदिश क्रमशः x,y और z हैं, तब 2x+y+z का मान है।
02:56View Solutionकिसी त्रिभुज की ऊँचाई और आधार क्रमशः 8 cm व 3 cm हैं, उसका क्षेत्रफल होगा :
01:48View SolutionA, B and C spend 80%, 85% and 75% of their incomes, respectively. If their savings are in the ratio 8:9:20 and the difference between the incomes of A and C is Rs. 18,000 , then the income of B is :
A, B और C अपनी आय का क्रमशः 80%, 85% और 75% खर्च करते हैं | यदि उनकी बचत 8 : 9 : 20 के अनुपात में है और A तथा C की आय में 18000 रुपये का अंतर है, तो B की आय ज्ञात करें |01:43View SolutionA,B and C are three points on a circle such that the angles subtended by the chord AB and AC at the centre O are 110^@ and 130^@ respectively. Then the value of angle BAC is: A, B और C एक वृत्त पर स्थित तीन ऐसे बिंदु हैं कि जीवा AB और AC के द्वारा केंद्र O पर अंतरित किये गए कोण क्रमशः 110^@ तथा 130^@ हैं| angle BAC का मान है :
View SolutionLet A and B be two towers with the same base. From the mid point of the line joining their feet, the angle of elevation of the tops of A and b are 30^@ and 45^@ , respectively. The ratio of the heights of A and B is, A और B एक ही आधार के साथ दो टॉवर हैं। उनके आधार से जुड़ने वाली रेखा के मध्य बिंदु से, A और B के शीर्ष के कोण क्रमशः 30 और 45 हैं। A और B की ऊंचाइयों का अनुपात है ज्ञात करे |
View SolutionA' and 'B' are brothers. 'C' and 'D' are sisters. A's son is D's brother. How is B related to C ?
'A' और 'B' भाई हैं। 'C' और 'D' बहनें हैं। A का पुत्र D का भाई है। B का C से क्या संबंध है ?View SolutionC_xH_y कार्बन और हाइड्रोजन की दहन की ऊष्माएँ क्रमश: a, b और c cal हैं। C_xH_y की संभवन ऊष्मा होगी:
View Solutionतीन समतापीय आरेख (P बनाम V) A, B और C क्रमश: तीन तापमान T_1, T_2 और T_3 पर खींचे गए हैं। तापमान का सही क्रम होगा :
View Solutionयदि A और B, क्रमशः 10 और 20 BOD के साथ जल के दो नमूने हैं, तब सही विकल्प चिह्नित कीजिए।
View Solution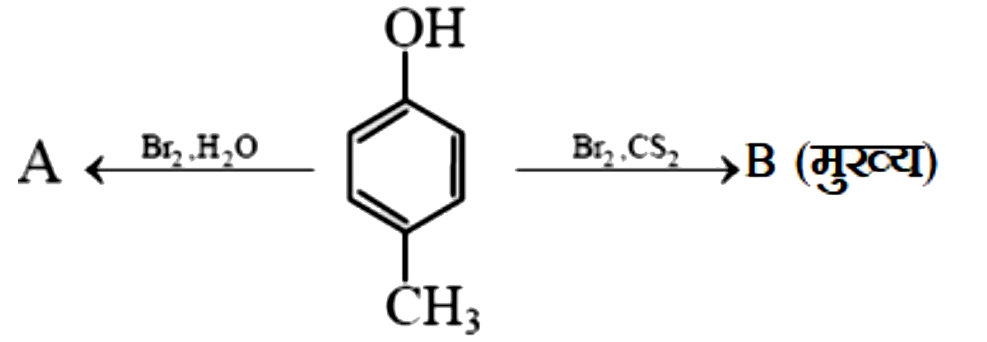
A और B क्रमश: हैंView Solutionसमान ताप पर दो अलग-अलग बल्बों में आदर्श गैसें A और B उपस्थित हैं। A का आण्विक द्रव्यमान गैस B का आधा है और गैस A का घनत्व गैस B का दोगुना है। A तथा गैस B के दाब का अनुपात है?
View Solutionअम्लीय, क्षारीय और उभयधर्मी ऑक्साइड, क्रमशः हैं:
View Solution

