A system is taken from state A to state B along two different paths 1 and 2 . The heat absorbed and work done by the system along these two paths are $Q_{1}$ and $W_{1}$ and $W_{2}$ respectively.

A

$Q_{1} = Q_{2}$

B

$Q_{1} + W_{1} = Q_{2} + W_{2}$

C

$Q_{1} - W_{1} = Q_{2} - W_{2}$

D

$W_{1} = W_{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

$Δ U = Q + W$
Path I: $[Q_{1} - W_{1}]$
$[∵ Q_{1} \to heat absorbed (+ v e), W_{1} \to Work done by the system (-ve)]$
Similarly,
Path II: $[Q_{2} - W_{2}]$
$∴ U$ is a state function $Δ U = Q_{1} - W_{1} = Q_{2} - W_{2}$

|

Updated on:21/07/2023

Class 12 CHEMISTRY THERMODYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A system is taken from state A to state N along two different paths 1 and 2. The heat absorbed and work done by system along these two paths are $Q_{1}$ and $Q_{2}$ , and $W_{1}$ and $W_{2}$ respectively. Then
A $Q_{1} = Q_{2}$
B $W_{1} = W_{2}$
C $Q_{1} - W_{1} = Q_{2} - W_{2}$
D $Q_{1} + W_{1} = Q_{2} + W_{2}$
Question 2 - Select One
A system is taken from state A to B through three different paths 1,2 and 3. The work done is maximum is :

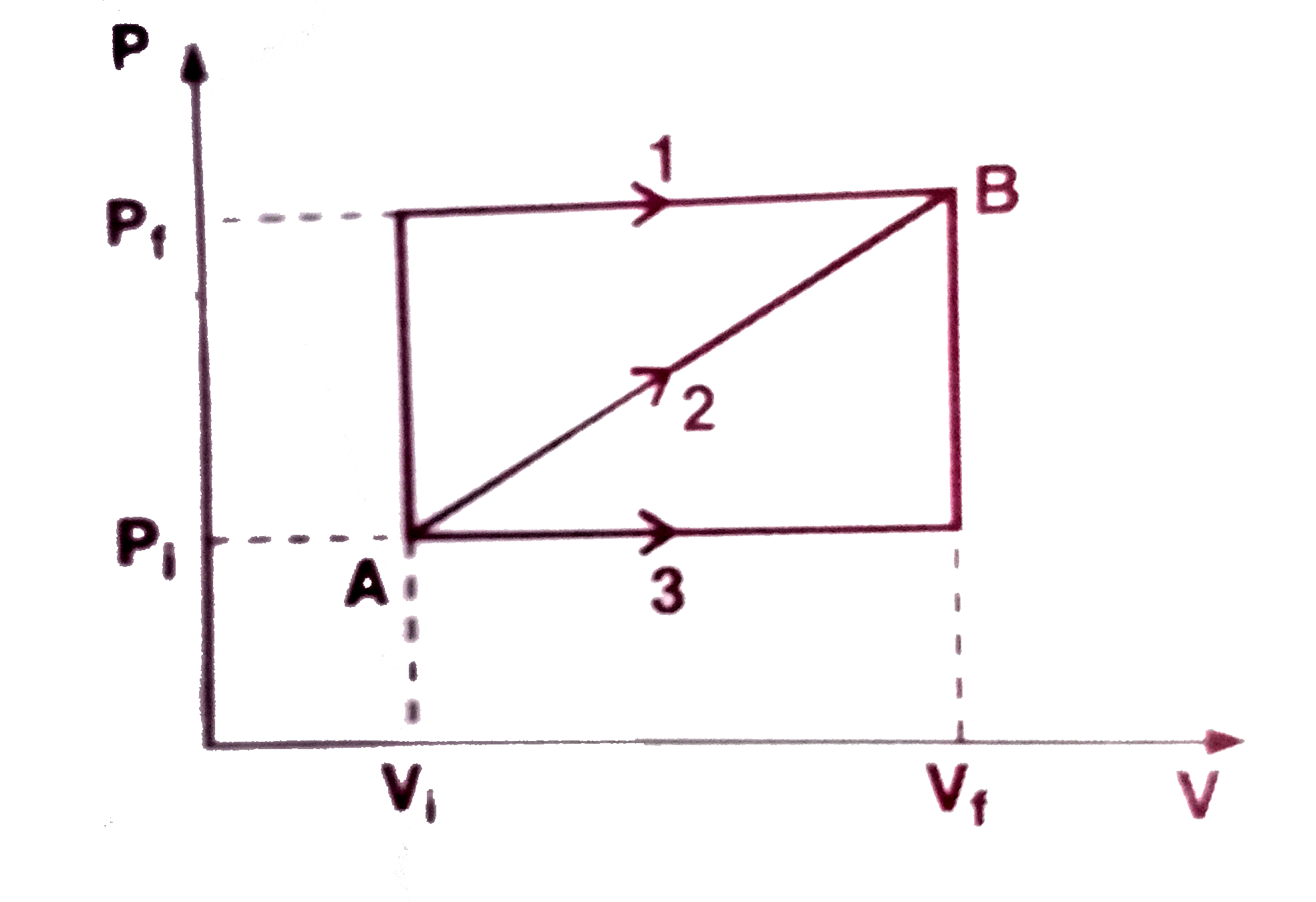Aprocess 1
Bprocess 2
Cprocess 3
Dequal in all magnitude
Question 3 - Select One
When a system is taken from stata a to state b along the path acb as shown in figure, 60 J of heat flows into the system and 30 J of work is done by the system. Along the path adb, if the work done by the system is 10 J, heat flow into the system is

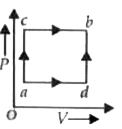A100 J
B20 J
C80 J
D40 J

MARVEL PUBLICATION-CHEMICAL THERMODYNAMICS AND ENERGETICS-MULTIPLE CHOICE QUESTIONS (HIGHER LEVEL)

Home
Ask Doubt
Profile