I is the incentre of .
Forces acting along IA,IB,IC respectively are in equilibrium. Then =
cos A : cos B : cos C
The correct Answer is:B
Topper's Solved these Questions
- VECTORSBOOK - MARVEL PUBLICATIONCHAPTER - VECTORSEXERCISE - PREVIOUS YEARS MHT-CET EXAM QUESTIONS
10 Videos
- VECTORSBOOK - MARVEL PUBLICATIONCHAPTER - VECTORSEXERCISE - TEST YOUR GRASP
20 Videos
- TRIGONOMETRIC FUNCTIONSBOOK - MARVEL PUBLICATIONCHAPTER - TRIGONOMETRIC FUNCTIONSEXERCISE - TEST YOUR GRASP: CHAPTER 3-3.3
13 Videos
Similar Questions
ABC is a triangle. Forces P, Q, R acting along the lines OA, OB and OC are in equilibrium. Then P:Q:R= …..
If O is the incentre of ΔABC
View Solution'I' is the incentre of triangle ABC whose corresponding sides are a,b,c, rspectively. a→IA+b→IB+c→IC is always equal to a. →0 b. (a+b+c)→BC c. (→a+→b+→c)→AC d. (a+b+c)→AB
View Solution
Knowledge Check
If 3¯¯¯P+2¯¯¯R−5¯¯¯Q=¯0, then
AP,Q,R are collinearBP,Q,R vertices of a ΔCQ divides PR externallyDNone of theseLet ¯a,¯b,¯c be three coplanar unit vectors such that ¯a+¯b+¯c=¯c. If three vectors ¯p,¯q,¯r parallel to ¯a,¯b,¯c respectively and having integral but different magnitudes , then among the following options |¯p+¯q+¯r| can take a value equal to
A1B0C√3D2ABC is an isosceles triangle right angled at A. forces of magnitude 2√2,5and6 act along BC, CA and AB respectively. The magnitude of their resultant force is
A4B5C11+2√2D30
If f is the centre of a circle inscribed in a triangle ABC, then ∣∣∣−−→BC∣∣∣−→IA+∣∣∣−−→CA∣∣∣−→IB+∣∣∣−−→AB∣∣∣−→IC is
View SolutionABC is an isosceles triangle right angled at A. forces of magnitude 2√2,5and6 act along BC, CA and AB respectively. The magnitude of their resultant force is
View SolutionABCD is a rigid square of side 1 metre. Forces of 2,5, 6 and 3 kg wt. act along the sides AB, BC, CD and DA respectively and two forces of 4√2kg. wt. each act along AC and DB. The magnitude, direction and line of action of the resultant are ........... , ............
View SolutionConsider △ABC. Let I bet he incentre and a,b,c be the sides of the triangle opposite to angles A,B,C respectively. Let O be any point in the plane of △ABC within the triangle. AO,BO and CO meet the sides BC, CA and AB in D,E and F respectively. a−→IA=b−→IB+c−→IC= (A) −1(B)0(C)1(D)3
View Solution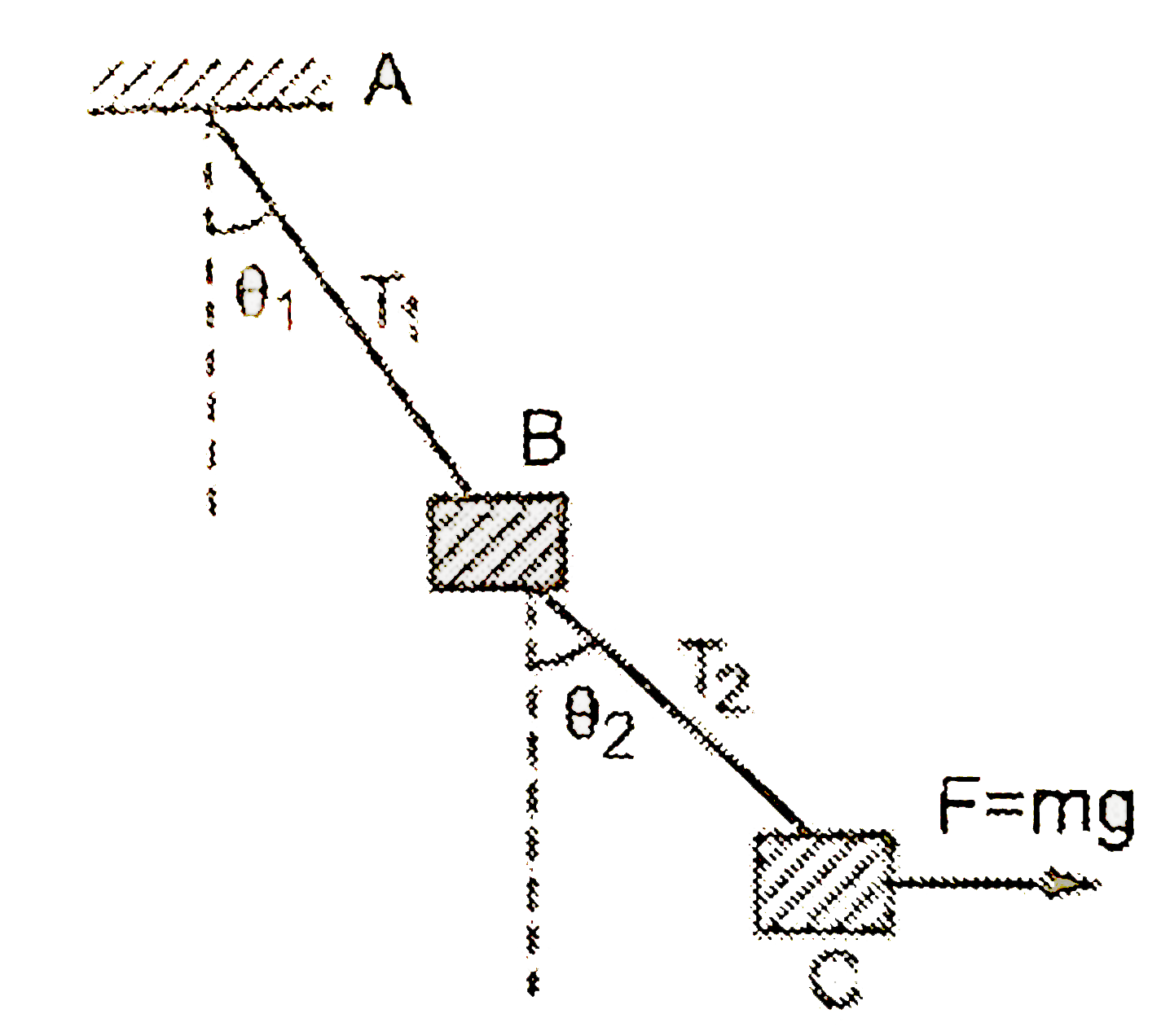
The blocks B and C in the figure have mass m each. The strings AB and BC are light, having tensions T1 and T2 respectively. The system is in equilibrium with a constant horizontal force mg acting on C.
View Solution
