A cylindrical vessel of radius r is filled with a homogeneous liquid upto a height h. It is found that the force exerted by the liquid column on the bottom of the cylinder is equal to the force exerted by the liquid on the sides of the cylinder. What is the relation between r and h?
r=h
r=2h
The correct Answer is:D
To solve the problem, we need to find the relationship between the radius r of a cylindrical vessel and the height h of the liquid it contains, given that the force exerted by the liquid column on the bottom of the cylinder is equal to the force exerted by the liquid on the sides of the cylinder.
Step 1: Calculate the force exerted by the liquid column on the bottom of the cylinder.
The force exerted by the liquid column on the bottom can be calculated using the formula:
Fbottom=Pressure×Area
The pressure at the bottom due to the liquid column is given by:
P=ρgh
where:
- ρ = density of the liquid,
- g = acceleration due to gravity,
- h = height of the liquid column.
The area A of the bottom of the cylinder (which is circular) is:
A=πr2
Thus, the force on the bottom becomes:
Fbottom=ρgh⋅πr2
Step 2: Calculate the force exerted by the liquid on the sides of the cylinder.
The force exerted by the liquid on the sides of the cylinder can be calculated by considering the pressure at a height y from the bottom, which is:
P(y)=ρgy
The differential force dF acting on a small strip of the side of the cylinder of height dy and circumference 2πr is:
dF=P(y)⋅Area of the strip=ρgy⋅(2πr⋅dy)
To find the total force on the side, we integrate this from y=0 to y=h:
Fsides=∫h0ρgy(2πr)dy
Calculating the integral:
Fsides=2πrρg∫h0ydy=2πrρg(y22)h0=2πrρg⋅h22=πrρgh2
Step 3: Set the forces equal to each other.
According to the problem, these two forces are equal:
Fbottom=Fsides
Substituting the expressions we derived:
ρgh⋅πr2=πrρgh2
Step 4: Simplify the equation.
We can cancel out π, ρ, and g from both sides (assuming they are non-zero):
hr2=rh2
Step 5: Rearranging the equation.
Dividing both sides by r (assuming r≠0):
hr=h2
Now, dividing both sides by h (assuming h≠0):
r=h
Final Relation:
Thus, the relationship between the radius r and the height h is:
r=h
Fbottom=Pressure×Area
The pressure at the bottom due to the liquid column is given by:
P=ρgh
where:
- ρ = density of the liquid,
- g = acceleration due to gravity,
- h = height of the liquid column.
A=πr2
Thus, the force on the bottom becomes:
Fbottom=ρgh⋅πr2
P(y)=ρgy
The differential force dF acting on a small strip of the side of the cylinder of height dy and circumference 2πr is:
dF=P(y)⋅Area of the strip=ρgy⋅(2πr⋅dy)
To find the total force on the side, we integrate this from y=0 to y=h:
Fsides=∫h0ρgy(2πr)dy
Calculating the integral:
Fsides=2πrρg∫h0ydy=2πrρg(y22)h0=2πrρg⋅h22=πrρgh2
Fbottom=Fsides
Substituting the expressions we derived:
ρgh⋅πr2=πrρgh2
hr2=rh2
hr=h2
Now, dividing both sides by h (assuming h≠0):
r=h
Thus, the relationship between the radius r and the height h is:
r=h
Topper's Solved these Questions
- FRICTIONAL IN SOLIDS AND LIQUIDS BOOK - MARVEL PUBLICATIONCHAPTER - FRICTIONAL IN SOLIDS AND LIQUIDS EXERCISE - TEST YOUR GRASP
10 Videos
- FORCE, WORK AND TORQUEBOOK - MARVEL PUBLICATIONCHAPTER - FORCE, WORK AND TORQUEEXERCISE - TEST YOUR GRASP
10 Videos
- MAGNETIC EFFECT OF ELECTRIC CURRENT BOOK - MARVEL PUBLICATIONCHAPTER - MAGNETIC EFFECT OF ELECTRIC CURRENT EXERCISE - TEST YOUR GRASP
10 Videos
Similar Questions
To what height should a cyclindrical vessel be filled with a homogeneous liquid to make the force with which the liquid pressure on the sides of the vessel equal to the force exerted by the liquid on the bottom of the vessel ?
View SolutionA cylindrical vessel of radius R=1m and height H=3m is filled with an ideal liquid up to a height of h=2 m. the contaienr with liquid is rotated about its central vertical axis such that the liquid just rises to the brim. Calculate the angular speed (ω) of the container.
View Solution
Knowledge Check
To what height should a cyclindrical vessel be filled with a homogeneous liquid to make the force with which the liquid pressure on the sides of the vessel equal to the force exerted by the liquid on the bottom of the vessel ?
Aequal to the radiusBless than radiusCmore than radiusDfour times of radiusThe height to which a cylindrical vessel be filled with a homogenous liquid, to make the average force with which the liquid presses the side of the vessel equal to the force exerted by the liquid on the bottom of the vessel, is equal to.
Ahalf of the radius of the vesselBradius of the vesselCone-fourth of the radius of the vesselDthree-fourth of the radius of the vessel.A cylinder is fill ed with a liquid of density p upto a height h. What is the hydrostatic pressure exerted by the liquid on the bottom of the cylinder, if the cylinder is kept in a lifi moving upwa rds with an acceleration a ?
AρghBρ(g+a)Cρ(g−a)Dρgha
To what height should a cylindrical vessel be filled with a homogenous liquid to make to force on bottom equal to force on side? (R = radius of vessel )
View Solution_E01_126_Q01.png)
A massless conical flask filled with a liquid is kepth on t a table in a vacuum the force exerted by the liquid on the bse of the flask is W1. Th force exerted by the flask on the table is W2
View SolutionThe pressure exerted by a liquid of height h is given by(symbols have their usuall meanings)
View SolutionA cylinder is filled with non viscous liquid of density d to a hegiht h0 and a hole is made at a height h1 from the bottom of the cylinder. The velocity of liquid issuing out of the hole is
View SolutionA cylindrical vessel is filled with a liquid up to a height H. A small hole is made in the vessel at a distance y below the liquid surface as shown in figure. The liquid emerging from the hole strike the ground at distance x
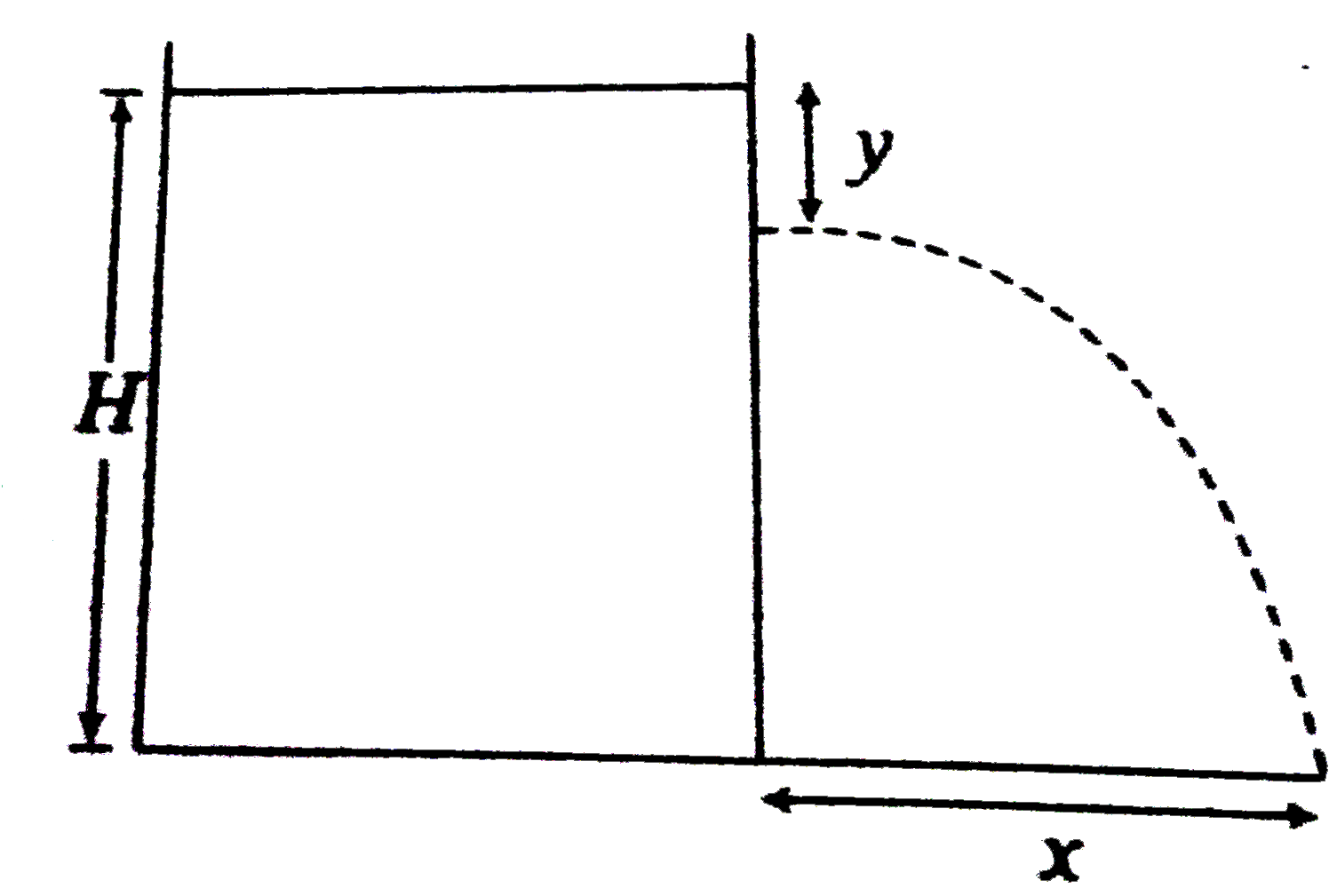
View Solution
