A double convex lens whose radii of curvature are R1 and R2 forms the image of a point object, placed on its axis. If the lens is revered, face to face, then the ratio of the distances of the images in the first and second case will be
R1R2
R2R1
1:1
2:1
The correct Answer is:C
To solve the problem, we need to analyze the behavior of a double convex lens when it is placed in two different orientations. We will derive the focal lengths and the corresponding image distances in both cases.
1. Understanding the Lens Formula:
The lens formula is given by:
1f=1v−1u
where f is the focal length, v is the image distance, and u is the object distance. For a double convex lens, the focal length can be calculated using the radii of curvature.
2. Focal Length Calculation:
The focal length f of a double convex lens is given by:
1f=(n−1)(1R1−1R2)
where n is the refractive index of the lens material, and R1 and R2 are the radii of curvature of the two surfaces of the lens.
3. First Case (Normal Orientation):
- When the lens is in its normal orientation, we denote the focal length as f1.
- The image distance v1 can be calculated using the lens formula, with the object distance u being negative (as per sign convention):
1f1=1v1−1(−u)
Rearranging gives:
v1=fuf+u
4. Second Case (Reversed Orientation):
- When the lens is reversed, the radii of curvature change places, so we denote the new focal length as f2:
1f2=(n−1)(1R2−1R1)
- The image distance v2 can be calculated similarly:
v2=f2uf2+u
5. Comparing the Two Cases:
- Since the focal lengths f1 and f2 are related by the same formula but with R1 and R2 swapped, we find that:
f1=f2
- Therefore, the image distances v1 and v2 will also be equal, leading to:
v1v2=1
6. Conclusion:
The ratio of the distances of the images in the first and second case is:
Ratio=1:1
Final Answer:
The ratio of the distances of the images in the first and second case is 1:1.
The lens formula is given by:
1f=1v−1u
where f is the focal length, v is the image distance, and u is the object distance. For a double convex lens, the focal length can be calculated using the radii of curvature.
The focal length f of a double convex lens is given by:
1f=(n−1)(1R1−1R2)
where n is the refractive index of the lens material, and R1 and R2 are the radii of curvature of the two surfaces of the lens.
- When the lens is in its normal orientation, we denote the focal length as f1.
- The image distance v1 can be calculated using the lens formula, with the object distance u being negative (as per sign convention):
1f1=1v1−1(−u)
Rearranging gives:
v1=fuf+u
- When the lens is reversed, the radii of curvature change places, so we denote the new focal length as f2:
1f2=(n−1)(1R2−1R1)
- The image distance v2 can be calculated similarly:
v2=f2uf2+u
- Since the focal lengths f1 and f2 are related by the same formula but with R1 and R2 swapped, we find that:
f1=f2
- Therefore, the image distances v1 and v2 will also be equal, leading to:
v1v2=1
The ratio of the distances of the images in the first and second case is:
Ratio=1:1
The ratio of the distances of the images in the first and second case is 1:1.
Topper's Solved these Questions
- BOOK - MARVEL PUBLICATIONCHAPTER - RAY OPTICS (MIRRORS, LENSES AND OPTICAL INSTRUMENTS)EXERCISE - TEST YOUR GRASP10videos
RAY OPTICS (MIRRORS, LENSES AND OPTICAL INSTRUMENTS)
- BOOK - MARVEL PUBLICATIONCHAPTER - MEASUREMENTS EXERCISE - TEST YOUR GRASP10videos
MEASUREMENTS
- BOOK - MARVEL PUBLICATIONCHAPTER - REFRACTION OF LIGHT EXERCISE - Test Your Grasp10videos
REFRACTION OF LIGHT
Similar Questions
A lens whose radii of curvature are different is forming the image of an object placed on its axis. If the lens is reversed, will the position of the image change ?
View SolutionA lens is forming the image of an object on its axis. If the lens is placed with its faces reversed, will the position of image change ?
View Solution
Knowledge Check
- Question 1 - Select One
A convex lens form a real image of a point object placed on its principal axis. If the upper half of the lens is painted black, the image will
ABe shifted downwardsBBe shifted upwardsCNot be shiftedDShift on the principal axis - Question 2 - Select One or More
A convex forms a real image of a poinnt object placed on its principal axis. If the upper half of the lens is painted black
Athe image will be shifted downwrdBthe image will be shifted upwardCthe image will not be shiftedDthe intensity of the imase will decrease - Question 3 - Select One
A convex lens forms a virtual image of an object placed ………… .
Aat infinityBbetween '2F1and'F1'Cat F1Dbetween 'F1' and optical centre 'O'
A lens is forming the image of an object on its axis. If the lens is placed with its faces reversed, will the position of image change ?
View SolutionA convex lens forms a virtual image of an object placed ………… .
View SolutionA convex lens is made up of three different materials as shown in the figure. For a point object placed on its axis, the number of images formed are
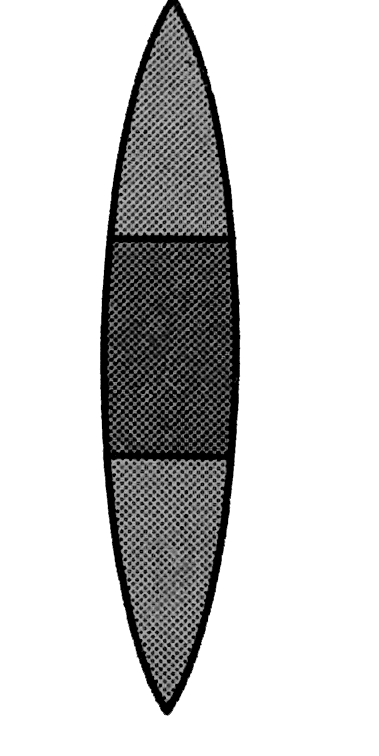 View Solution
View SolutionA convex lens forms a virtual image of an object placed…….. .
View SolutionA convex lens is made up of three different materials as shown in the figure. For a point object placed on its axis, the number of images formed are
 View Solution
View Solution

