The equation for the vibration of a string fixed at both ends vibrating in its third harmonic is given by y=2cm sin[(0.6cm−1)x]cos[(500πs−1)t]. The length of the string is
15.7 cm
20.6 cm
24.6 cm
12.5 cm
The correct Answer is:A
For the third harmonic, the string of length L , vibrates with 3 loops.
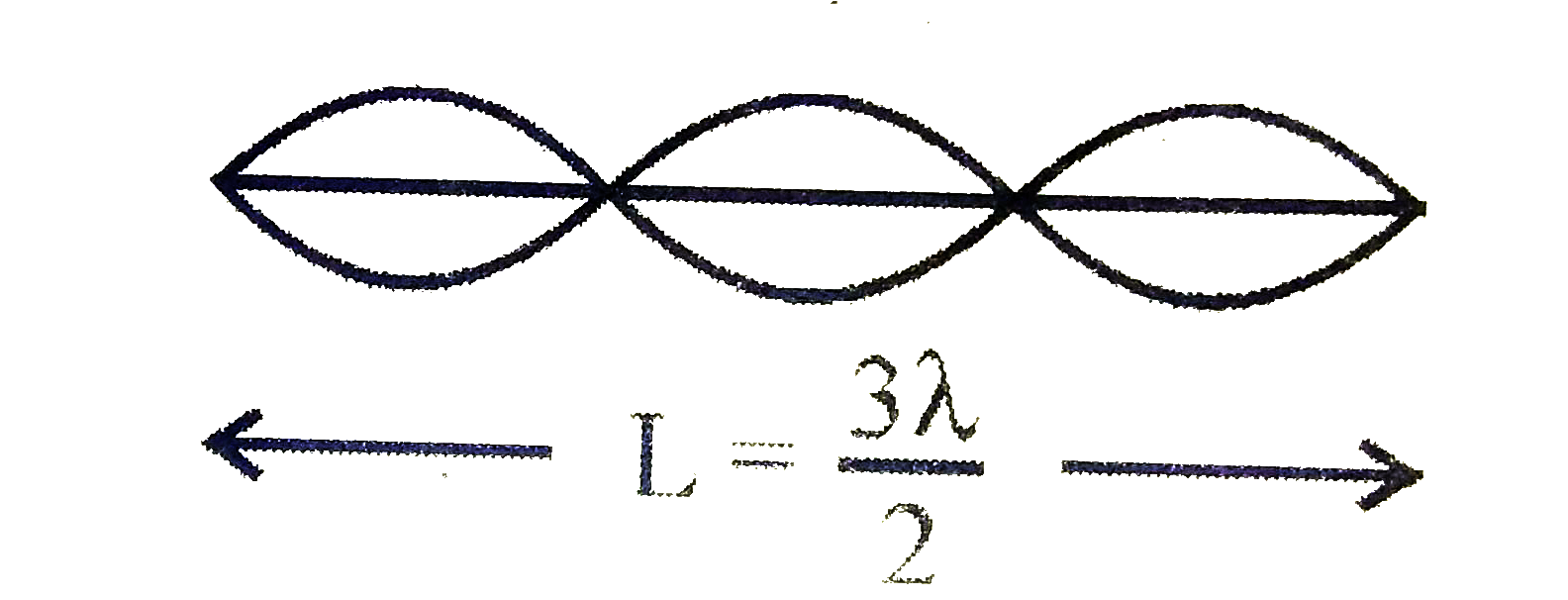
∴3λ2=L ∴λ2=L3
Comparing the equation y=2sin(0.6x)cos(500πt) with the standard equation
∴y=2Acos(2πxλ)sin(2πtT)
we get 2πxλ=0.6x∴2πλ=0.06∴λ=2π0.6
∴L=3λ2=32(2π0.6)=3π0.6
=5π=5×3.14=15.7 cm
Topper's Solved these Questions
- BOOK - MARVEL PUBLICATIONCHAPTER - STATIONARY WAVESEXERCISE - MULTIPLE CHOICE QUESTIONS (STANDARD LEVEL )75videos
STATIONARY WAVES
- BOOK - MARVEL PUBLICATIONCHAPTER - STATIONARY WAVESEXERCISE - MULTIPLE CHOICE QUESTIONS (GRAPHICAL )1videos
STATIONARY WAVES
- BOOK - MARVEL PUBLICATIONCHAPTER - STATIONARY WAVESEXERCISE - MULTIPLE CHOICE QUESTIONS ( STANDARD LEVEL )65videos
STATIONARY WAVES
- BOOK - MARVEL PUBLICATIONCHAPTER - SEMICONDUCTORS EXERCISE - MCQs261videos
SEMICONDUCTORS
- BOOK - MARVEL PUBLICATIONCHAPTER - SURFACE TENSION EXERCISE - MULTIPLE CHOICE QUESTIONS . (TEST YOUR GRASP )10videos
SURFACE TENSION
Similar Questions
The equation for the vibration of a string, fixed at both ends vibrating in its third harmonic, is given by y=(0.4cm)sin[(0.314cm−1)x]cos[f(600πs−1)t].(a) What is the frequency of vibration ? (b) What are the positions of the nodes ? (c) What is the length of the string ? (d) What is the wavelength and the speed of two travelling waves that can interfere to give this vibration ?
View SolutionThe equation of a standing wave, produced on a string fixed at both ends, is y=(0.4cm)sin[(0.314cm−1)x]cos[(600πs−1)t] What could be the smallest length of the string ?
View Solution
Knowledge Check
- Question 1 - Select One
The equation for the vibration of a string fixed at both ends vibrating in its second harmonic is given by y=2sin(0.3cm−1)xcos((500πs−1)t)cm. The length of the string is :
A24.6cmB12.5cmC20.6 cmD15.7 cm - Question 2 - Select One
the equation for the vibration of a string fixed both ends vibration in its third harmonic is given by
y = 2 cm sin [(0.6cm−1)×]cos[(500ps−1t]A24.6 cmB12.5 cmC20 . 6 cmD15. 7 cm - Question 3 - Select One
The equation of the standing wave in a string clamped at both ends, vibrating in its third harmonic is given by
y=0.4sin(0.314x)cos(600πt)
where, x and y are in cm and t in sec.
(a) the frequency of vibration is 300Hz
(b) the length of the string is 30cm
(c) the nodes are located at x=0, 10cm, 30cmAOnly a is trueBa,b are trueCb,c are trueDa,b,c are true
The equation of a stationary wave on a string clamped at both ends and vibrating in its third harmonic is given by y=0.5sin(0.314x)cos(600πt) where x and y are in cm and t is in sec. What is the length of the string?
View SolutionA string fixed at its both ends vibrates in 5 loops as shown in the figure. The number of nodes and antinodes respectively
 View Solution
View SolutionA string is clamped at both the ends and it is vibrating in its 4th harmonic. The equation of the stationary wave is Y=0.3sin(0.157x)cos(200πt). The length of the string is: (All quantities are in SI units.)
View SolutionA string of length L fixed at both ends vibrates in its first overtone. Then the wavelength will be
View SolutionIf a string fixed at both ends, vibrates in its fourth harmonic, the wavelength is 15 cm. What is the length of the string ?
View Solution

