A capacitor is used to store 24 watt hour of enegy at 1200 volt. What should be the capacitance of the capacitor?
120mF
120μF
24μF
24mF
The correct Answer is:A
To find the capacitance of a capacitor that stores 24 watt-hours of energy at 1200 volts, we can follow these steps:
Step 1: Convert watt-hours to joules
The energy stored in the capacitor is given in watt-hours. We need to convert this to joules since the standard unit of energy in physics is joules.
Energy (in joules)=Energy (in watt-hours)×3600seconds
Given that the energy is 24 watt-hours:
Energy=24Watt-hours×3600seconds=86400Joules
Step 2: Use the formula for energy stored in a capacitor
The energy E stored in a capacitor is given by the formula:
E=12CV2
Where:
- E is the energy in joules,
- C is the capacitance in farads,
- V is the voltage in volts.
Step 3: Rearrange the formula to solve for capacitance
We need to rearrange the formula to solve for C:
C=2EV2
Step 4: Substitute the known values
Now we can substitute the values we have into the equation. We have E=86400J and V=1200V:
C=2×8640012002
Step 5: Calculate the capacitance
Now we can calculate C:
C=1728001440000
C=0.12F=120mF
Conclusion
The capacitance of the capacitor should be 120mF (millifarads).
---
The energy stored in the capacitor is given in watt-hours. We need to convert this to joules since the standard unit of energy in physics is joules.
The energy E stored in a capacitor is given by the formula:
- E is the energy in joules,
- C is the capacitance in farads,
- V is the voltage in volts.
We need to rearrange the formula to solve for C:
Now we can substitute the values we have into the equation. We have E=86400J and V=1200V:
Now we can calculate C:
The capacitance of the capacitor should be 120mF (millifarads).
Topper's Solved these Questions
- BOOK - MARVEL PUBLICATIONCHAPTER - ELECTROSTATICSEXERCISE - TEST YOUR GRASP20videos
ELECTROSTATICS
- BOOK - MARVEL PUBLICATIONCHAPTER - ELECTRONS AND PHOTONS EXERCISE - TEST YOUR GRASP - 1715videos
ELECTRONS AND PHOTONS
- BOOK - MARVEL PUBLICATIONCHAPTER - GRAVITATION EXERCISE - TEST YOUR GRASP -220videos
GRAVITATION
Similar Questions
Knowledge Check
- Question 1 - Select One
A 10μF capacitor is charged to a potential difference of 50V and is connected to another uncharged capacitor in parallel. Now the common potential difference becomes 20 volt. The capacitance of second capacitor is
A10μFB20μFC30μFD15μF - Question 2 - Select One
In parallel arrangement of capacitor,
i. the p.d across individual capacitor is same.
ii. The charge is shared by the capacitor in the ratio of the capacitance.
iii. The resultant capacitance is equal to sum of the capacitance of capacitors used.AOnly statement (i) is correct.BOnly statement (ii) is correct.COnly statement (iii) is correct.DAll three statements are correct.
A potential difference of 20 volts develops between the plates of the capacitor when 2×1012 electrons are transferred from one plate of the capacitor to the other. What should be the capacitance of capacitor?
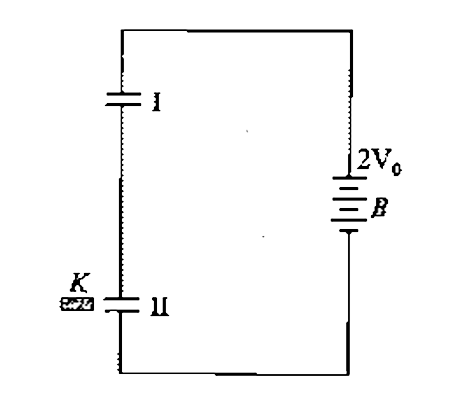
View SolutionTwo identical capacitors are connected as shown in fignre. A dielectric slab is introduced between the plates of one of the capacitors so as to fill the gap, the battery remaining connected. What will be the capacitance, the charge, potential difference and stored energy for each capacitor?
 View Solution
View SolutionA capacitor charged from a 50 V d.c. supply is found to have charge of 10μC. What is the capacitance of the capacitor and how much energy is stored in it?
View SolutionThe capacitance of a charged capacitor is C and the energy stored in it is U. What is the value of charge on the capacitor?
View SolutionA capacitor of capacitance 5 μF is charged to a potential difference of 10 volts and another capacitor of capacitance 9 μF is charged to a potential difference of 8 volts. Now these two capacitors are connected in such a manner that the positive plate of one is connected to the positive plate of other. Calculate the common potential difference across the two capacitors.
View SolutionA parallel plate capacitor has plates of area 4m2 separated by distance of 0.5 mm. The capacitor is connected across a cell of emf 100 V.
Find the capacitance, charge and energy stored in the capacitor.View Solution