The internal energy of one mole of a gas is
The correct Answer is:A
Internal energy 1 mole gas =3/2 RT
Topper's Solved these Questions
- Chemical Thermodynamics & EnergeticsBOOK - NIKITA PUBLICATIONCHAPTER - Chemical Thermodynamics & EnergeticsEXERCISE - QUESTION FROM COMPETITIVE EXAM
35 Videos
- CHEMICAL KINETICS BOOK - NIKITA PUBLICATIONCHAPTER - CHEMICAL KINETICS EXERCISE - MCQs
351 Videos
- CHEMISTRY IN EVERYDAY LIFE BOOK - NIKITA PUBLICATIONCHAPTER - CHEMISTRY IN EVERYDAY LIFE EXERCISE - MCQs
224 Videos
Similar Questions
An ideal gas is in thermodynamic equilibrium. The number of degrees of freedom of a molecule of the gas is n.The internal energy of one mole of the gas is Un and the speed of sound in the gas is vn.At a fixed temperature and pressure, which of the following is the correct option?
View SolutionCalculate the internal energy of one mole of a diatomic gas at 300 K. Assume the molecules to be rigid.
View Solution
Knowledge Check
The internal energy of one mole of ideal gas is
A3/2RTB1/2kTC1/2RTD3/2kTThe internal energy of one mole of ideal gas is
A32RTB12KTC12RTD32KTThe molar specific heat of a gas at constant volume is 24 J/mol K. then change in its internal energy if one mole of such gas is heated at constant from 10∘C to 30∘C is
A240 JB480 JC360 JD720 J
Consider a P−V diagram in which the path followed by one mole of perfect gas in a cyclinderical container is shown in (figure)
(a) Find the work done when the gas is taken from state 1 to state 2.
(b) What is the ratio of temperatures T1/T2,ifV2=2V1?
(c ) Given the internal energy for one mole of gas at temperature Tis(3/2)RT, find the heat supplied to the gas when it is taken from state 1 to 2, with V2=2V1.
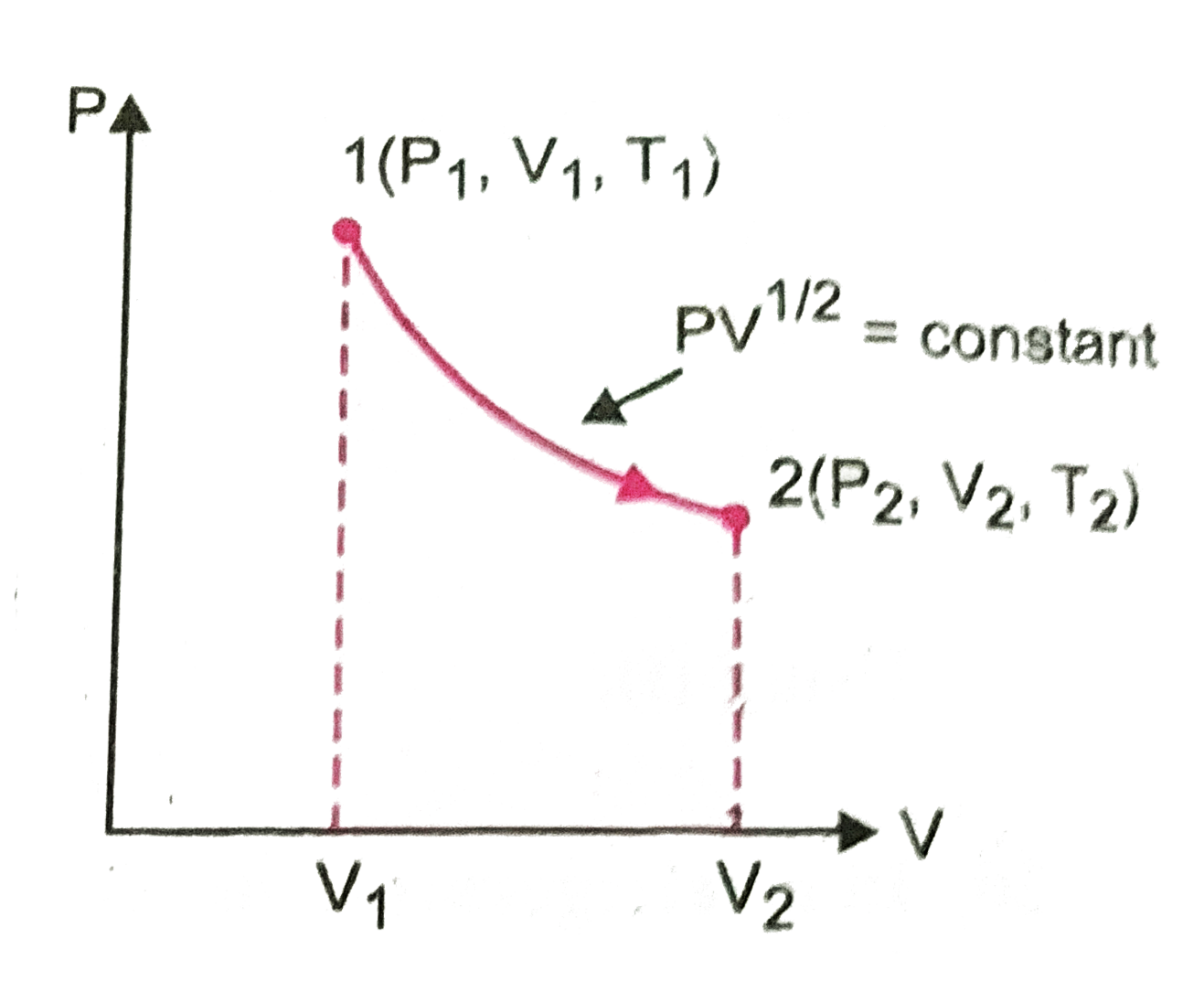
View SolutionThe internal energy of one mole of the diatomic gas at 200 K is
View SolutionThe total internal energy of one mole of rigid diatomic gas is
View SolutionThe ratio of translational and rotational kinetic energies at 100K temperature is 3:2. Then the internal energy of one mole gas at that temperature is (R=8.3j/mol−K]
View SolutionThe kinetic energy of one mole of any gas depends upon
View Solution
