The point on a circle nearest to the point P(2,1) is at a distance of 4 units and the farthest point is (6, 5). Then find the equation of the circle.
(3+√2,2+√2)
(2+√2,3+√2)
(4+√2,3+√2)
(3+√2,4+√2)
The correct Answer is:C
Step by step video, text & image solution for The point on a circle nearest to the point P(2,1) is at a distance of 4 units and the farthest point is (6, 5). Then find the equation of the circle. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ARIHANT MATHSCHAPTER - CIRCLE EXERCISE - Exercise For Session 316videos
CIRCLE
- BOOK - ARIHANT MATHSCHAPTER - CIRCLE EXERCISE - Exercise For Session 417videos
CIRCLE
- BOOK - ARIHANT MATHSCHAPTER - CIRCLE EXERCISE - Exercise For Session 118videos
CIRCLE
- BOOK - ARIHANT MATHSCHAPTER - BIONOMIAL THEOREMEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)21videos
BIONOMIAL THEOREM
- BOOK - ARIHANT MATHSCHAPTER - COMPLEX NUMBERSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)43videos
COMPLEX NUMBERS
Similar Questions
The normal at the point (3, 4) on a circle cuts the circle at the point (-1,-2). Then the equation of the circle is
View SolutionThe equation of radical axis of two circles is x+y=1. One of the circles has the ends ofa diameter at the points (1,−3)and(4,1) and the other passes through the point (1, 2).Find the equating of these circles.
View Solution
Knowledge Check
- Question 1 - Select One
If (4,3) and (-12,-1) are the end points of a diameter of a circle then the equation of the circle is
Ax2+y2−8x−2y−51=0Bx2+y2+8x−2y−51=0Cx2+y2+8x+2y−51=0Dnone of these
(i) Find the equation of a circle passes through the origin and cuts the intercepts of 6 units and 8 units on X-axis and Y-axis respectively.
(ii) Find the equation of a circle which passes through the two points on y-aixs whose distance from origin is 4 units and radius is 5 units.View SolutionThe foot of the normal from the point (1,2) to a circle is (3,4) and a diameter of the circle has the equation 2x+y+5=0 ,then the equation of the circle is
View SolutionThe length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
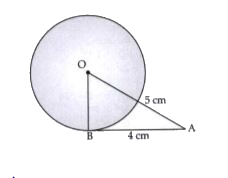 View Solution
View SolutionThe length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm . Find the radius of the circle.
 View Solution
View SolutionA) The radius of a circle is 5 cm. At this point The tangent is drawn if the length of the tangent is 12 cm. Find the distance from the center of the circle to the point.
View SolutionFind the equation of the circle passing through the point (−2,1) and touching the line 3x−2y−6=0 at the point (4,3).
View SolutionThe length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
View Solution

