A line L passeds through the points (1,1)and(2,0) and another line L' passes through (12,0) and perpendicular to L. Then the area of the triangle formed by the lines L, L' and Y-axis is
158
254
258
2516
The correct Answer is:D
Step by step video, text & image solution for A line L passeds through the points (1,1) and (2,0) and another line L' passes through ((1)/(2), 0) and perpendicular to L. Then the area of the triangle formed by the lines L, L' and Y-axis is by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- STRAIGHT LINE BOOK - TARGET PUBLICATIONCHAPTER - STRAIGHT LINE EXERCISE - COMPETITIVE THINKING
99 Videos
- SETS, RELATIONS AND FUNCTIONSBOOK - TARGET PUBLICATIONCHAPTER - SETS, RELATIONS AND FUNCTIONSEXERCISE - EVALUATION TEST
14 Videos
- TRIGONOMETRIC FUNCTIONS OF COMPOUND ANGLES BOOK - TARGET PUBLICATIONCHAPTER - TRIGONOMETRIC FUNCTIONS OF COMPOUND ANGLES EXERCISE - EVALUATION TEST
12 Videos
Similar Questions
A line L passes through the points (1, 1) and (0, 2) and another line M which is perpendicular to L passes through the point (0,-12).The area of the triangle formed by these lines with y-axis is- (A) 25/8 (B) 25/16 (C) 25/4 (D) 25/32
View SolutionIn the xy plane, the line L1 passes through the point (1,1) and the line L2 passes through the point (−1,1). If the difference of the slopes of the lines is 2. Then the locus of the point of intersection of the lines L1andL2 is
View Solution
Knowledge Check
The area of triangle formed by the lines l1andl2 and the x-axis is:
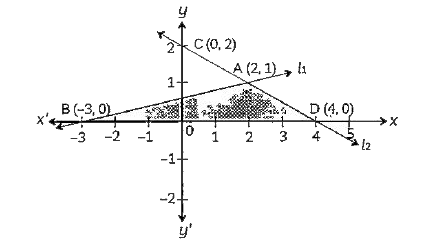 A7 sq. unitsB92 sq.unitsC72 sq.unitsD4 sq. units
A7 sq. unitsB92 sq.unitsC72 sq.unitsD4 sq. unitsA straight line L is perpendicular to the line 5x -y =1 . The area of the triangle formed by the line L and coordinate axes is 5. Find the equation to the line :
Ax+5y=±5√2Bx - 3y = 0C2x + y = 0Dx+4y=5√2A straight line L is perpendicular to the line 5x -y =1 . The area of the triangle formed by the line L and coordinate axes is 5. Find the equation to the line :
Aa. x+5y=±5√2Bb. x−3y=0Cc. 2x+y=0Dd. x+4y=5√2
L1 is a line passing through the point A(n,n+1) having slope, n,L2 is a line passing through the point B(−n,n2) and is perpendicular to L1, If L1 and L2 intersect on y-axis, then n is equal to ________ (n>0)
View SolutionA straight line L is perpendicular to the line 5x−y=1 . The area of the triangle formed by line L, and the coordinate axes is 5. Find the equation of line L.
View SolutionThe line l1 passing through the point (1,1) and the 'l2' passes through the point (−1,1) If the difference of the slope of lines is 2. Find the locus of the point of intersection of the l1 and l2
View SolutionEquation of a line passing through the point (2,−3,2) and equally inclined to the line L1andL2 may be equal to :
View SolutionLying in the plane x+y+z=6 is a line L passing through (1, 2, 3) and perpendicular to the line of intersection of planes x+y+z=6 and 2x−y+z=4, then the equation of L is
View Solution
