Mr . A gave his telephone number to Mr . B .Mr . B remembers that the first two digits were 40 and the remaining four digits were two 3s, one 6 and one 8 . He is not certain about the order of the digits . Mr. B dials 403638. The probability that he will get A ' s house is
12
14
18
112
The correct Answer is:D
To solve the problem, we need to determine the probability that Mr. B dials the correct telephone number of Mr. A, given the information he remembers.
1. Identify the Known Information:
- The first two digits of the telephone number are 40.
- The remaining four digits consist of two 3s, one 6, and one 8.
2. List the Remaining Digits:
- The remaining digits are: 3, 3, 6, 8.
3. Calculate the Total Arrangements of the Remaining Digits:
- Since there are 4 digits where '3' is repeated twice, we can use the formula for permutations of multiset:
Total arrangements=n!n1!⋅n2!⋯nk!
where n is the total number of items to arrange, and n1,n2,…,nk are the counts of each distinct item.
- Here, n=4 (total digits), n1=2 (for the two 3s), and n2=1 (for 6), n3=1 (for 8).
- Thus, the total arrangements can be calculated as:
Total arrangements=4!2!⋅1!⋅1!=242=12.
4. Determine the Number of Successful Outcomes:
- There is only 1 specific arrangement that corresponds to Mr. A's telephone number, which is 403638.
5. Calculate the Probability:
- The probability P that Mr. B dials the correct number is given by the ratio of successful outcomes to total outcomes:
P=Number of successful outcomesTotal arrangements=112.
Final Answer:
The probability that Mr. B will get Mr. A's house is 112.
---
- The first two digits of the telephone number are 40.
- The remaining four digits consist of two 3s, one 6, and one 8.
- The remaining digits are: 3, 3, 6, 8.
- Since there are 4 digits where '3' is repeated twice, we can use the formula for permutations of multiset:
Total arrangements=n!n1!⋅n2!⋯nk!
where n is the total number of items to arrange, and n1,n2,…,nk are the counts of each distinct item.
- Here, n=4 (total digits), n1=2 (for the two 3s), and n2=1 (for 6), n3=1 (for 8).
- Thus, the total arrangements can be calculated as:
Total arrangements=4!2!⋅1!⋅1!=242=12.
- There is only 1 specific arrangement that corresponds to Mr. A's telephone number, which is 403638.
- The probability P that Mr. B dials the correct number is given by the ratio of successful outcomes to total outcomes:
P=Number of successful outcomesTotal arrangements=112.
The probability that Mr. B will get Mr. A's house is 112.
Topper's Solved these Questions
- BOOK - TARGET PUBLICATIONCHAPTER - PROBABILITYEXERCISE - CRITICAL THINKING (ADDITION THEOREM AND CONDITIONAL PROBABILITY)31videos
PROBABILITY
- BOOK - TARGET PUBLICATIONCHAPTER - PROBABILITYEXERCISE - CRITICAL THINKING (BAYES THEOREM AND ODDS)13videos
PROBABILITY
- BOOK - TARGET PUBLICATIONCHAPTER - PROBABILITYEXERCISE - CLASSICAL THINKING (BAYES THEOREM AND ODDS )4videos
PROBABILITY
- BOOK - TARGET PUBLICATIONCHAPTER - FACTORIZATION FORMULAEEXERCISE - EVALUATION TEST8videos
FACTORIZATION FORMULAE
- BOOK - TARGET PUBLICATIONCHAPTER - SETS, RELATIONS AND FUNCTIONSEXERCISE - EVALUATION TEST14videos
SETS, RELATIONS AND FUNCTIONS
Similar Questions
An old man while dialing a 7 digit telephone humber remembcrs that the first four digits consists of one I's, one 2's and two 3's. He also remembers that the fifth digit is cither a 4 or 5 while has no memorising of the sixth digit, he remembers that the seventh digit is 9 minus the sixth digit. Maximum number of distinet trials he has to try to make sure that he dials the correct telephone number, is
View SolutionOn one page of a telephone directory , there were 200 telephone numbers . The frequency distribution of their unit's digits is given in the following table :

Out of the numbers on the page , a number is chosen at random .
What is the probability that the unit's digit of the chosen number is
(i) 6 ? (ii) a non zero multiple of 3 ?
(iii) a nonzero even number ? (iv) an odd number ?View Solution
Knowledge Check
- Question 1 - Select One
In a game of six digits, two digits are already fixed for prize. If any one will find these two fixed digits then he will win the prize. Mr. A selects two numbers. The probability that Mr. A will win the prize is
A115B16C15D11 - Question 2 - Select One
identify following statements for true (T) and and False (F):
S1: An old man while dialing a 7-digit telephone number remembers that the first four digits consist of one 1's, one 2's and two 3's. he also remembers that the fifth digit is either a 4 or 5 while has no memory of the sixt digit, he remembers that the seventh digit is 9 minus the sixth digit, maximum number of distinct trials he has to try to make sure that he dials the correct telephone number, is 240. S2: A woman has 11 close friends. the number of ways in which she can invite 5 of them to dinner, if two of them are not on speaking terms and will not attend together is 378.
S3: 10 IIT and 2 PET students sit in a row. if the total number of ways in which exactly 3 IIT students sit between 2 PET students is λ×10!, then λ is 6. which of the following choice is correct?ATTTBTTFCTFFDFTF - Question 3 - Select One
Mr. A randomly picks 3 distinct numbers from the set {1, 2, 3, 4, 5, 6, 7, 8, 9} and arranges them in descending order to form a three digit number. Mr. B randomly picks 3 distinct numbers from the set {1, 2, 3, 4, 5, 6, 7, 8} and also arranges them in descending order to form a 3 digit number.
Q. The probability that Mr. A's number is larger than Mr. B's number, is :A3756B3956C3156Dnone of these
Amrish wakes up in the morning and notices that his digital cock recde 07: 25 am. After noon, he looks at the clock again.
What is the probability that
the number in column B is 8 ?
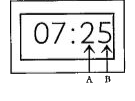 View Solution
View SolutionIn a number of three digits, the digits in the unit’s place and in the hundred’s place are equal and the sum of all the digits is 8. The number of such numbers is a. 3 b. 4 c. 5 d. 6
View SolutionShubham has to make a telephone call to his friend Nisheeth, Unfortunately he does not remember the 7 digit phone nu is exactly one 9 in the num is a four digit number of the form abcd then c equal. mber. But he remembers that the first three digits are 635 or 674, the number is odd and there ber. The maximum number of trials that Shubham has to make to be successful
View SolutionMr. A randomly picks 3 distinct numbers from the set {1, 2, 3, 4, 5, 6, 7, 8, 9} and arranges them in descending order to form a three digit number. Mr. B randomly picks 3 distinct numbers from the set {1, 2, 3, 4, 5, 6, 7, 8} and also arranges them in descending order to form a 3 digit number.
Q. The probability that Mr. A's 3 digit number is always greater than Mr. B's 3 digit number is :View SolutionMr. A randomly picks 3 distinct numbers from the set {1, 2, 3, 4, 5, 6, 7, 8, 9} and arranges them in descending order to form a three digit number. Mr. B randomly picks 3 distinct numbers from the set {1, 2, 3, 4, 5, 6, 7, 8} and also arranges them in descending order to form a 3 digit number.
Q. The probability that A and B has the same 3 digit number is :View Solution

