In a class, 40% of students study maths and science and 60 % of student study maths. What is the probability of a student studying science given the student is already studying maths?
13
16
23
15
The correct Answer is:C
To solve the problem step by step, we can use the concept of conditional probability. We need to find the probability of a student studying Science given that the student is already studying Maths.
Step 1: Define the Events
Let:
- M = Event that a student studies Maths
- S = Event that a student studies Science
Step 2: Identify Given Probabilities
From the problem statement, we know:
- P(M∩S)=0.4 (Probability that a student studies both Maths and Science)
- P(M)=0.6 (Probability that a student studies Maths)
Step 3: Use the Formula for Conditional Probability
We need to find P(S|M), which is the probability of a student studying Science given that the student studies Maths. The formula for conditional probability is given by:
P(S|M)=P(M∩S)P(M)
Step 4: Substitute the Known Values
Now, we can substitute the values we have into the formula:
P(S|M)=P(M∩S)P(M)=0.40.6
Step 5: Simplify the Expression
Now we simplify the fraction:
P(S|M)=0.40.6=46=23
Step 6: Conclusion
Thus, the probability of a student studying Science given that the student is already studying Maths is:
P(S|M)=23
Let:
- M = Event that a student studies Maths
- S = Event that a student studies Science
From the problem statement, we know:
- P(M∩S)=0.4 (Probability that a student studies both Maths and Science)
- P(M)=0.6 (Probability that a student studies Maths)
We need to find P(S|M), which is the probability of a student studying Science given that the student studies Maths. The formula for conditional probability is given by:
Now, we can substitute the values we have into the formula:
Now we simplify the fraction:
Thus, the probability of a student studying Science given that the student is already studying Maths is:
Topper's Solved these Questions
- PROBABILITYBOOK - TARGET PUBLICATIONCHAPTER - PROBABILITYEXERCISE - COMPETITIVE THINKING (MISCELLANEOUS)
3 Videos
- PROBABILITYBOOK - TARGET PUBLICATIONCHAPTER - PROBABILITYEXERCISE - EVALUATION TEST
8 Videos
- PROBABILITYBOOK - TARGET PUBLICATIONCHAPTER - PROBABILITYEXERCISE - COMPETITIVE THINKING (ALGEBRA OF EVENTS , CONCEPT OF PROBABILTIY)
42 Videos
- FACTORIZATION FORMULAEBOOK - TARGET PUBLICATIONCHAPTER - FACTORIZATION FORMULAEEXERCISE - EVALUATION TEST
8 Videos
- SETS, RELATIONS AND FUNCTIONSBOOK - TARGET PUBLICATIONCHAPTER - SETS, RELATIONS AND FUNCTIONSEXERCISE - EVALUATION TEST
14 Videos
Similar Questions
In a class, 40% students study mathematics, 25% study biology and 15 % study both mathematics and biology. One student is selected at random. Find the probability that
(i) he studies mathematics if it is known that he studies biology
(ii) he studies biology if it is known that he studies mathematics.
View SolutionIn a class, 80% of students pass in maths exam and 70% of students pass in English exam. 10% of students fail in Both subjects and if 144 students pass in Both subejects. Find the total number of students.
View Solution
Knowledge Check
In a class of 50 students, 30 study Basic, 25 study Pascal and 10 study both How many study neither?
A15B0C5D35In an examination 50% of the students passed in maths, 55% of the students passed in english 40% of the students passed in Hindi. If 15% of the students passed in maths and english , 20% of the students passed in english and hindi and 25% of the students passed in maths and hindi and 10% of the students passed in all the three subjects then find the % of students who failed in all three subjects ?
A11%B7%C9%D5%In class XI of a school,40% of the students study Mathematics and 30% study Biology. If a student is selected at random from the class, then find the probability that he will be studying Mathematics or Biology
A0.5B0.6C0.65DNone of these
In class XI of a school 40% of the students study Mathematics and 30% study Biology. 10% of the class study both mathematics and biology. If a student is selected at random from the class, find the probability that he will be studying Mathematics or Biology or both.
View SolutionIn a University there are 1200 students studying four different subjects, Mathematics, Statistics, Physics and Chemistry. 20% of the total number of students are studying Mathematics, one-fourth of the total number of students are studying Physics, 320 students are studying Statistics and remaining students are studying Chemistry. Three-fifth of the total number of students studying Chemistry are girls. 150 boys are studying Mathematics. 60% of students studying Physics are boys. 250 girls are studying Statistics.
What is the total number of boys studying Statistics and Physics ?
View SolutionIn a class of 50 students ,each student passed Maths of English ,If 10 students passed Maths ,then find the number of students who passed English
View SolutionThe following table indicates the number of students studying in three disciplines in five colleges
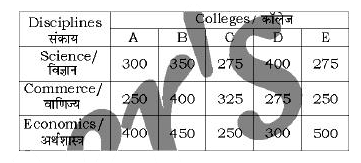
What is the ratio of the total number of students studying in the science stream to that of studying in commerce stream in all five colleges taken together?
View SolutionThe following table indicates the number of students studying in three disciplines in five colleges:
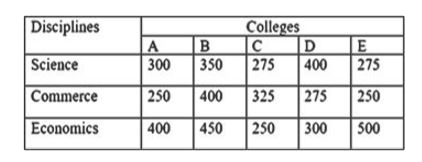
What is the ratio of the total number of students studying in the science stream to that of studying in commerce stream in all five colleges taken together?
View Solution
