Doubtnut Promotions Sticky

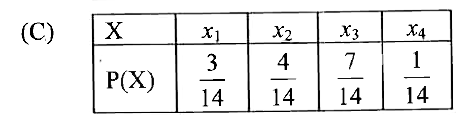
Let X be a random variable which assumes values x1,x2,x3, x4 such that 2P(X=x1)=3P(X=x2)=P(X=x3)=5P(X=x4). Find the probability distribution of X.

A

ocr_image

B

ocr_image

C

ocr_image

D

ocr_image

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:A

|
Answer

Step by step video, text & image solution for Let X be a random variable which assumes values x_1, x_2, x_3,\ x_4 such that 2P(X=x_1)=3P(X=x_2)=P(X=x_3)=5P(X=x_4)dot Find the probability distribution of X. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023
Class 12MATHSPROBABILITY

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Question 1 - Select One

    For the p.m.f. P (X = x) of discrete random variable X which takes values 1, 2, 3, 4 such that 2P(X=1)=3P(X=2)=P(X=3)=4P(X=4), then E (X)=

    A315
    B625
    C3125
    D6225
  • Question 2 - Select One

    A random variable X takes the value 1,2,3 and 4 such that
    2P(X=1)=3P(X=2)=P(X=3)=5P(X=4). If σ2 is the variance and μ is the mean of X then σ2+μ2=

    A42161
    B57061
    C14961
    D34803721
  • Question 3 - Select One

    If the random variable X takes the values x1,x2,x3……x10 with probabilities P(X=x1)=ki then the value of k is

    A(1/10)
    B(1/4)
    C(1/55)
    D(7/12)