In turbulent flow the velocity of the liquid molecules in contact with the walls of the tube.
is zero
is maximum
is equal to critical velocity
may have any value
The correct Answer is:D
Step by step video, text & image solution for In turbulent flow the velocity of the liquid molecules in contact with the walls of the tube. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- FRICTION IS SOLIDS AND LIQUIDS BOOK - TARGET PUBLICATIONCHAPTER - FRICTION IS SOLIDS AND LIQUIDS EXERCISE - MCQ (COMPETITIVE THINKING)
97 Videos
- FRICTION IS SOLIDS AND LIQUIDS BOOK - TARGET PUBLICATIONCHAPTER - FRICTION IS SOLIDS AND LIQUIDS EXERCISE - MCQ (EVALUATION TEST)
21 Videos
- FRICTION IS SOLIDS AND LIQUIDS BOOK - TARGET PUBLICATIONCHAPTER - FRICTION IS SOLIDS AND LIQUIDS EXERCISE - MCQ (EVALUATION TEST)
21 Videos
- FORCE BOOK - TARGET PUBLICATIONCHAPTER - FORCE EXERCISE - Evaluation Test
16 Videos
- MAGNETIC EFFECT OF ELECTRIC CURRENT BOOK - TARGET PUBLICATIONCHAPTER - MAGNETIC EFFECT OF ELECTRIC CURRENT EXERCISE - Evaluation Test
12 Videos
Similar Questions
The liquid is flowing steadily through a tube of varying diameter. How are the velocity of liquid flow (V) in any portion and the diameter (D) of the tube in that portion are related?
View SolutionA fluid is flowing through a tube of length L. The radius of the tube is r and the velocity of the fluid is v. If the radius of the tube is increased to 2r, then what will be the new velocity?
View Solution
Knowledge Check
In laminar flow of fluid, the velocity of the fluid in contact with the walls of the tube is
AmaximumBbetween 0 and maximumCequal to critical velocityDzeroIn stremline flow, the velocity of a liquid at a given point is
Aconstant in magnitude only.Bconstant in direction but not constnat in magnitufe.Cnot constnat in direction but constnat in magnitude.Dalways constant in magnitude and direction.For turbulent flow, the value of Reynolds number is
ARe>2000BRe<2000C1000<Re<2000DRe=1000
When a liquid moves steadily under some pressure through a horizontal tube, it moves in the form of cylindrical layers coaxial to the ends of the tube. The velocity of different layers is different. The velocity of the layer is maximum along the axis of the tube and it decreases as one moves towards the walls of the tube. According to Poiseuille, the rate of flow of liquid through a horizontal capillary tube varies as the relation Vαpr4ηl where l and r are the length and radius of the tube and p is the pressure different between the ends of the tube and is the constant of proportionality.
When two capillary tubes through which the liquid is flowing are joined in series then the equivalent liquid resistance is
View SolutionWhen a liquid moves steadily under some pressure through a horizontal tube, it moves in the form of cylindrical layers coaxial to the ends of the tube. The velocity of different layers is different. The velocity of the layer is maximum along the axis of the tube and it decreases as one moves towards the walls of the tube. According to Poiseuille, the rate of flow of liquid through a horizontal capillary tube varies as the relation Vαpr4ηl where l and r are the length and radius of the tube and p is the pressure different between the ends of the tube and is the constant of proportionality.
The dimensional formula for rate of flow
View SolutionWhen a liquid moves steadily under come pressure through a horizontal tube, it moves in the form of cylindrical layers coaxial to the exds of the tube. The velocity of different layers is different. The velocity of the layer is maximum along the axis of the tube and it decreases as one moves towards the walls of the tube. According to Poiseuille, the rate of flow of liquid through a horizontal capillary tube varies as the relation Vαpr4ηl where l and rare the length and radius of the tube and p is the pressure different between the ends of the tube and is the constant of proportionality.
Which of the following is correct:
View SolutionWhen a liquid moves steadily under some pressure through a horizontal tube, it moves in the form of cylindrical layers coaxial to the ends of the tube. The velocity of different layers is different. The velocity of the layer is maximum along the axis of the tube and it decreases as one moves towards the walls of the tube. According to Poiseuille, the rate of flow of liquid through a horizontal capillary tube varies as the relation Vαpr4ηl where l and r are the length and radius of the tube and p is the pressure different between the ends of the tube and is the constant of proportionality.
πpr48ηl is dimensionally equivalent to (R is the resistance)
View SolutionA liquid flows through a horizontal tube. The velocities of the liquid in the two sections, which have areas of cross section A1 and A2 are v1 and v2 respectively. The difference in the levels of the liquid in the two vertical tubes is h. Then
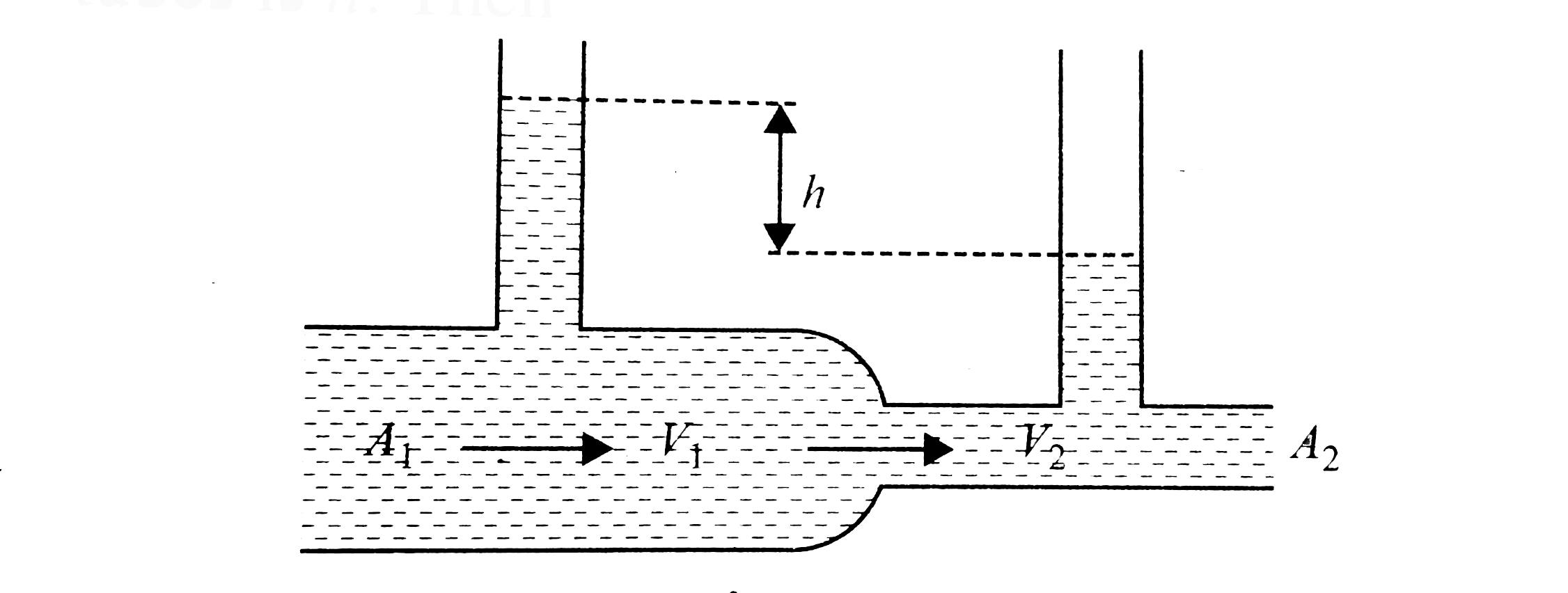
View Solution
