The coefficient of friction between m2 and inclined plane is μ (shown in the figure). If m1m2=sinθ then
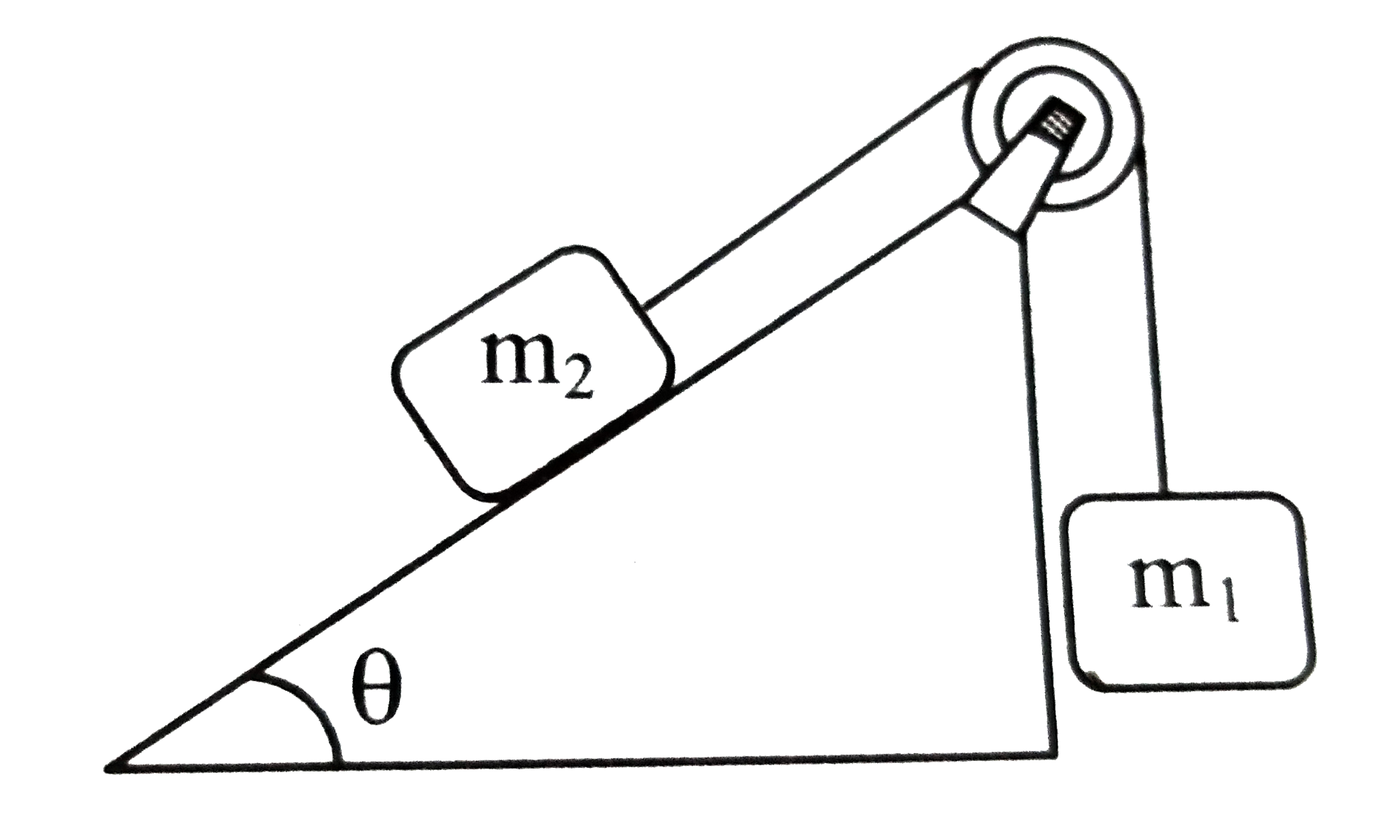
no motion takes place.
m1 moves downward.
m1 moves upward.
no sufficient incormation.
The correct Answer is:A
Step by step video & image solution for The coefficient of friction between m_(2) and inclined plane is mu (shown in the figure). If (m_(1))/(m_(2))=sin theta then by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- FRICTION IS SOLIDS AND LIQUIDS BOOK - TARGET PUBLICATIONCHAPTER - FRICTION IS SOLIDS AND LIQUIDS EXERCISE - MCQ (COMPETITIVE THINKING)
97 Videos
- FRICTION IS SOLIDS AND LIQUIDS BOOK - TARGET PUBLICATIONCHAPTER - FRICTION IS SOLIDS AND LIQUIDS EXERCISE - MCQ (EVALUATION TEST)
21 Videos
- FRICTION IS SOLIDS AND LIQUIDS BOOK - TARGET PUBLICATIONCHAPTER - FRICTION IS SOLIDS AND LIQUIDS EXERCISE - MCQ (EVALUATION TEST)
21 Videos
- FORCE BOOK - TARGET PUBLICATIONCHAPTER - FORCE EXERCISE - Evaluation Test
16 Videos
- MAGNETIC EFFECT OF ELECTRIC CURRENT BOOK - TARGET PUBLICATIONCHAPTER - MAGNETIC EFFECT OF ELECTRIC CURRENT EXERCISE - Evaluation Test
12 Videos
Similar Questions
Knowledge Check
Two block of masses M1 and, M2 are connected with a string which passed over a smooth pulley . The mass M1 is placed on a tough inclined plane as shown in figure .The coefficient of friction between and block and the inclined plane is μ what should be the minimum mass M2 so that the block M1 slides upwards?
 AM2=M1(sinθ+μcosθ)BM2=M1(sinθ−μcosθ)CM2=M1sinθ+μcosθDM2=M1sinθ−μcosθ
AM2=M1(sinθ+μcosθ)BM2=M1(sinθ−μcosθ)CM2=M1sinθ+μcosθDM2=M1sinθ−μcosθ
Two blocks of masses m1 and m2 connected by a string are placed gently over a fixed inclined plane, such that the tension in the connecting string is initially zero. The coefficient of friction between m1 and inclined plane is μ1, between μ2 and the inclined plane is μ2. The tension in the string shall continue to remain zero ifAμ1>tanα and μ2tanβBμ1<tanα and μ2>tanβCμ1>tanα and μ2tanβDμ2>tanα and μ2>tanβTwo blocks are kept on an inclined plane and tied to each other with a mass-less string. Coefficient of friction between m1 and inclined plane is μ1 & that betweeb m2 & the inclined is μ2. Then :
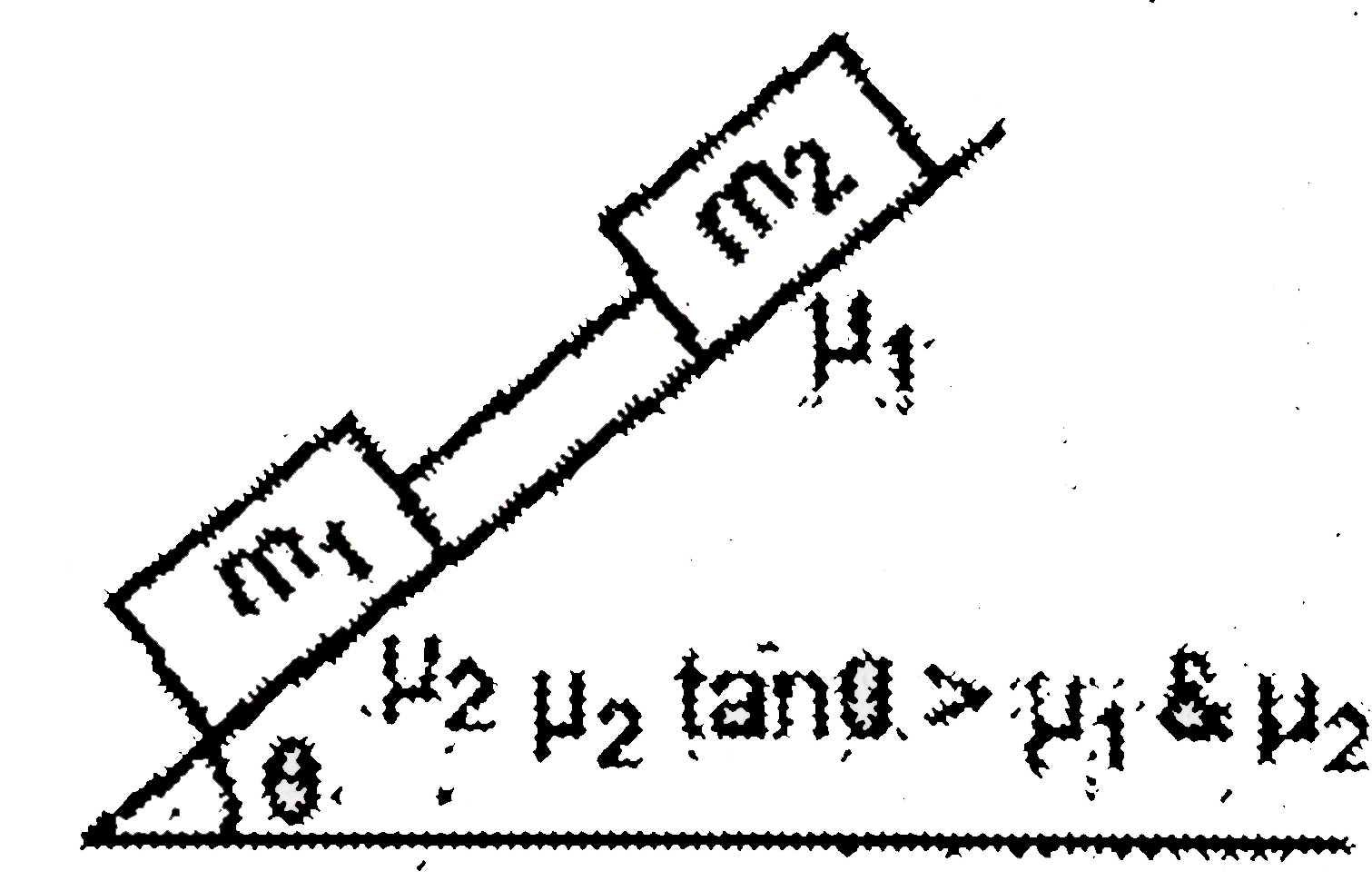 AThe tension in the string in zero if μ1>μ2BThe tension in the string is zero if μ1<μ2CTension in the string is always zero irrespective of μ1&μ2DNone of these
AThe tension in the string in zero if μ1>μ2BThe tension in the string is zero if μ1<μ2CTension in the string is always zero irrespective of μ1&μ2DNone of these
consider the situation shown in figure in which a block 'A' of mass 2 kg is placed over a biock.'B' of mass 4 kg. The combination of the blocks are placed on a inclined plane of inclination 37∘ with horizontal. The coefficient of friction between block B and inclined plane is μ2 and in between the two, blocks is μ1. The system is released from rest.
(Take g=10m/sec2)
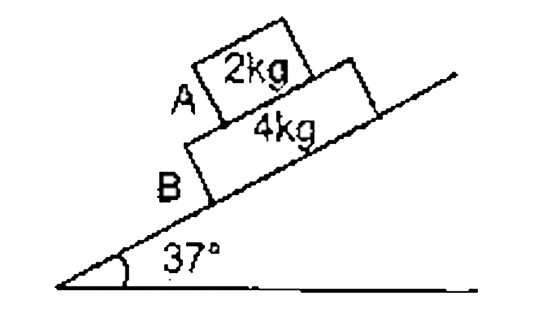
In the previous question the frictional force between block B and plane is :
View SolutionConsider the situation shown in figure in which a book 'A' of mass 2kg is placed over a block 'B' of mass 4kg. The combination of the placed on a inclined plane of inclination 37∘ with horizontal. The coefficient of friction between blocks B and inclined plane is μ2 and in between the two bolcks is μ1, The system is released from rest.
( Take g=10m/sec2)

In the previous question the frictional force between block B and plane is:
View SolutionConsider the situation shown in figure in which a book 'A' of mass 2kg is placed over a block 'B' of mass 4kg. The combination of the placed on a inclined plane of inclination 37∘ with horizontal. The coefficient of friction between blocks B and inclined plane is μ2 and in between the two bolcks is μ1, The system is released from rest.
( Take g=10m/sec2)

If μ1=0.8,μ2=0.8 then:
View SolutionConsider the situation shown in figure in which a book 'A' of mass 2kg is placed over a block 'B' of mass 4kg. The combination of the placed on a inclined plane of inclination 37∘ with horizontal. The coefficient of friction between blocks B and inclined plane is μ2 and in between the two bolcks is μ1, The system is released from rest.
( Take g=10m/sec2)

If μ1=0.5,μ2=0.5, then:
View SolutionA block of mass m is placed on a rough plane inclined at an angle θ with the horizontal. The coefficient of friction between the block and inclined plane is μ . Ifθ<tan−1(μ) , then net contact force exerted by the plane on the block is :
View Solution
