For thin prism angle of minimum deviation(delta) is given by

The correct relation between the refractive index ( $μ$ ) of the material of prism (A) and angle of minimum deviation ( $δ$ ) is
A $μ = \frac{sin (\frac{A}{2})}{sin (A + \frac{δ}{2})}$
B $μ = \frac{cos (A + \frac{δ}{2})}{sin (\frac{A}{2})}$
C $μ = \frac{cos (\frac{A}{2})}{sin (A + \frac{δ}{2})}$
D $μ = \frac{sin (A + \frac{δ}{2})}{sin (\frac{A}{2})}$
Assertion : Refractive index of material of a prism depends on angle of prism A and angle of minimum deviation $δ_{m}$ .
Reason : Because $μ = \frac{\frac{sin (A + δ_{m})}{2}}{sin A / 4}$
AIf both Assertion & Reason are True & Reason is a correct explanation of the Assertion.
BIf both Assertion & Reason are True but Reason is not a correct explanation of the Assertion.
CIf Assertion is True but the Reason is False.
DIf both Assertion & Reason are False.
For a small angled prism, angle of prism $A$ of minimum deviation $(δ)$ varies with the refractive index of the prism as shown in the graph

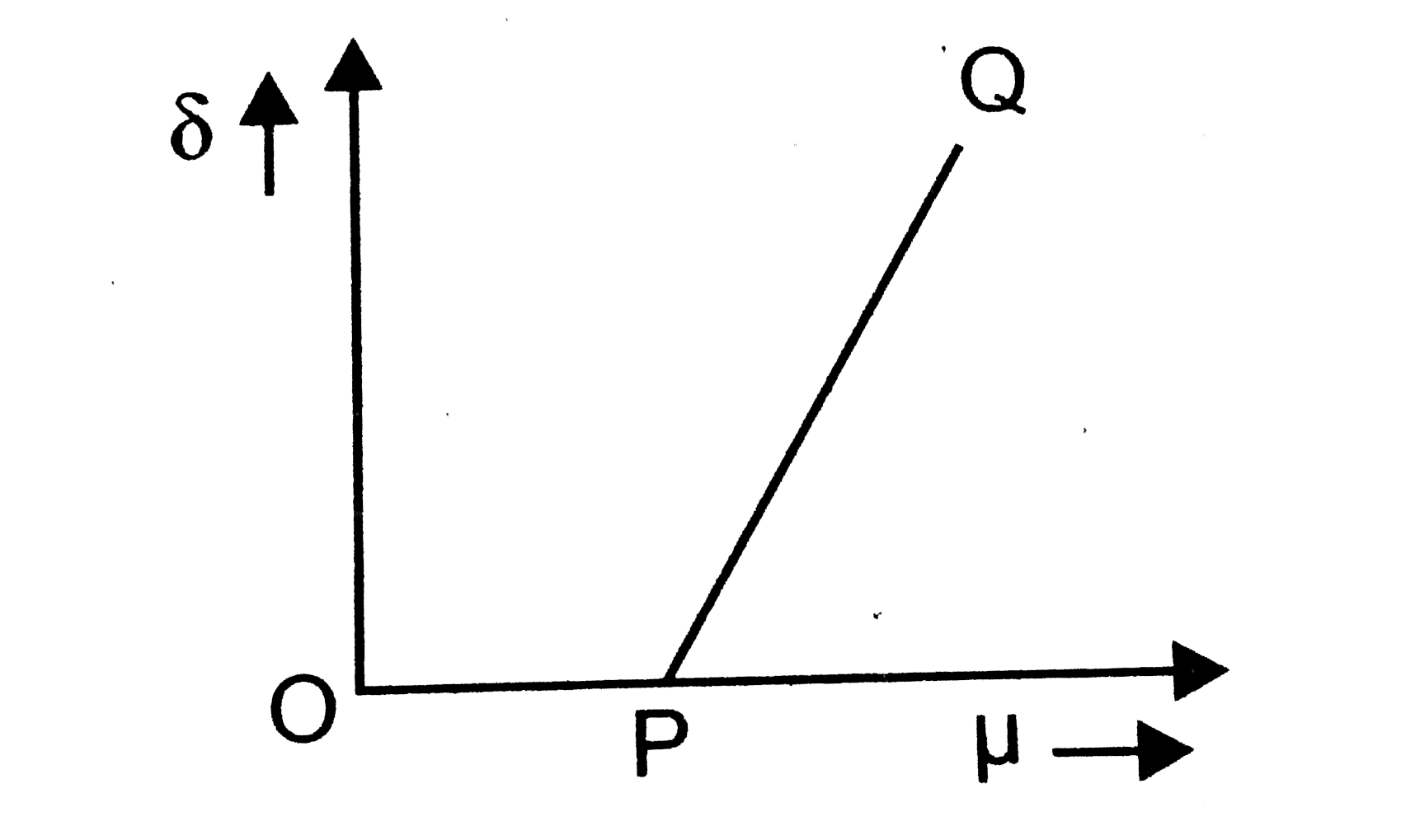APoint $P$ corresponds to $m = 1$
BSlope of the line $P Q = A / 2$
CSlope $= 2 A$
DNone of the above statements is true

For thin prism angle of minimum deviation( $δ$ ) is given by