When the bob of a conical pendulam is moving in a horizontal circle at constant speed, which quantity is fixed?
velocity
Acceleration
Centripetal force
Kinetic energy
The correct Answer is:D
To determine which quantity is fixed when the bob of a conical pendulum is moving in a horizontal circle at constant speed, we can analyze the situation step by step.
1. Understanding the Conical Pendulum:
- A conical pendulum consists of a mass (bob) attached to a string that traces out a horizontal circle while the string makes a constant angle with the vertical.
2. Analyzing Velocity:
- The bob moves with a constant speed in a circular path. While the speed (magnitude of velocity) is constant, the direction of the velocity vector changes continuously as the bob moves around the circle. Therefore, the velocity as a vector quantity is not fixed.
3. Analyzing Acceleration:
- The bob experiences centripetal acceleration directed towards the center of the circular path. Although the magnitude of this acceleration can remain constant if the speed is constant, its direction changes continuously as the bob moves around the circle. Thus, acceleration is not fixed.
4. Analyzing Centripetal Force:
- The centripetal force acts towards the center of the circular path and is responsible for keeping the bob in circular motion. Similar to acceleration, while the magnitude of the centripetal force can remain constant, its direction changes as the bob moves. Therefore, centripetal force is not fixed.
5. Analyzing Kinetic Energy:
- Kinetic energy (KE) is given by the formula KE=12mv2. Here, m (mass of the bob) is constant and v (speed) is also constant. Since both the mass and the speed are constant, the kinetic energy remains constant. Therefore, kinetic energy is the quantity that is fixed.
Conclusion:
The quantity that remains fixed when the bob of a conical pendulum is moving in a horizontal circle at constant speed is kinetic energy.
---
- A conical pendulum consists of a mass (bob) attached to a string that traces out a horizontal circle while the string makes a constant angle with the vertical.
- The bob moves with a constant speed in a circular path. While the speed (magnitude of velocity) is constant, the direction of the velocity vector changes continuously as the bob moves around the circle. Therefore, the velocity as a vector quantity is not fixed.
- The bob experiences centripetal acceleration directed towards the center of the circular path. Although the magnitude of this acceleration can remain constant if the speed is constant, its direction changes continuously as the bob moves around the circle. Thus, acceleration is not fixed.
- The centripetal force acts towards the center of the circular path and is responsible for keeping the bob in circular motion. Similar to acceleration, while the magnitude of the centripetal force can remain constant, its direction changes as the bob moves. Therefore, centripetal force is not fixed.
- Kinetic energy (KE) is given by the formula KE=12mv2. Here, m (mass of the bob) is constant and v (speed) is also constant. Since both the mass and the speed are constant, the kinetic energy remains constant. Therefore, kinetic energy is the quantity that is fixed.
The quantity that remains fixed when the bob of a conical pendulum is moving in a horizontal circle at constant speed is kinetic energy.
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - TARGET PUBLICATIONCHAPTER - CIRCULAR MOTIONEXERCISE - CRITICAL THINKING
93 Videos
- CIRCULAR MOTIONBOOK - TARGET PUBLICATIONCHAPTER - CIRCULAR MOTIONEXERCISE - COMPETITIVE THINKING
102 Videos
- ATOMS, MOLECULES AND NUCLEI BOOK - TARGET PUBLICATIONCHAPTER - ATOMS, MOLECULES AND NUCLEI EXERCISE - Evaluation test
19 Videos
- CURRENT ELECTRICITY BOOK - TARGET PUBLICATIONCHAPTER - CURRENT ELECTRICITY EXERCISE - Evaluation Test
6 Videos
Similar Questions
For a particle moving in a horizontal circle with constant angular velocity:
View SolutionFigure shows a conical pendulum, in which the bob (the small object at the lower end of the cord) moves in a horizontal circle at constant speed. (The cord sweeps out a cone as the bob rotates). The bob has a mass of 0.040 kg, the string has length L=0.90 m and negligible mass, and teh bob follows a circular path of circumfernece 0.94m. What are (a) The tension in the string and (b) the period of the motion?
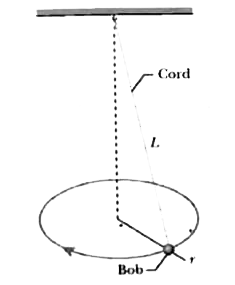
View Solution
Knowledge Check
A particle is moving in a horizontal circle with constant speed. It has constant
AVelocityBaccelerationCKinetic energyDDisplacementA particle is moving in a circle with a constant speed. Its moving is
APeriodicBOscillatoryCSimple harmonicDboth 'a' and 'b'A body is moving along circle at constant speed Which of the following statement is true?
Abody is not acceleratedBbody has a inward radial accelerationCbody has constant velocityDbody has outward radial acceleration.
A coical pendulum consists of a string of length L whose upper end is fixed and another end is tied to a bob. The bob is moving in horizontal circle with constant angular speed ω such that the string makes a constant angle θ with the verticle. calculate time period T0 of revolution of bob in terms of L,g and θ.
View SolutionIn the figure shown a lift goes downwards with a constant retardation. An observer in the lift observers a conical pendulam in the lift, revolving in a horizontal circle with time period 2 seconds. The distance between the centre of the circle and the point of suspension is 2.0 m. the retardation of the lift in m/s2 is
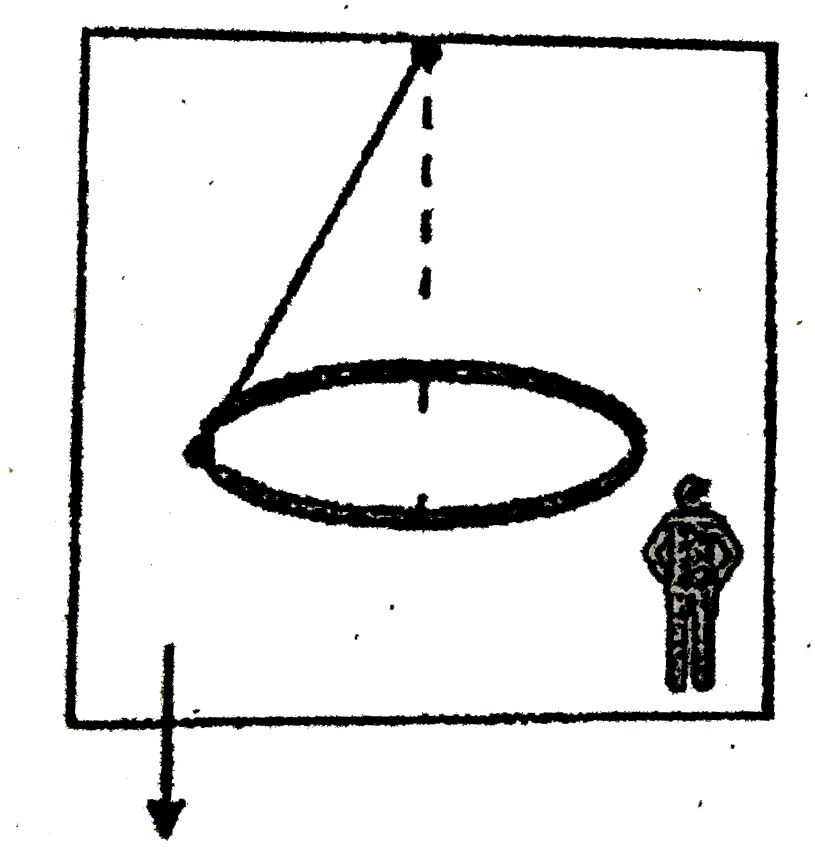
View SolutionA particle is moving in a circle with a constant speed, the acceleration of the particle has
View SolutionA conical pendulum consists of a simple pendulum moving in a horizontal circle as shown in the figure. C is the pivot, O the centre of the circle in which the pendulum bob moves and ω the constant angular velocity of the bob. If →L is the angular momentum about point C, then
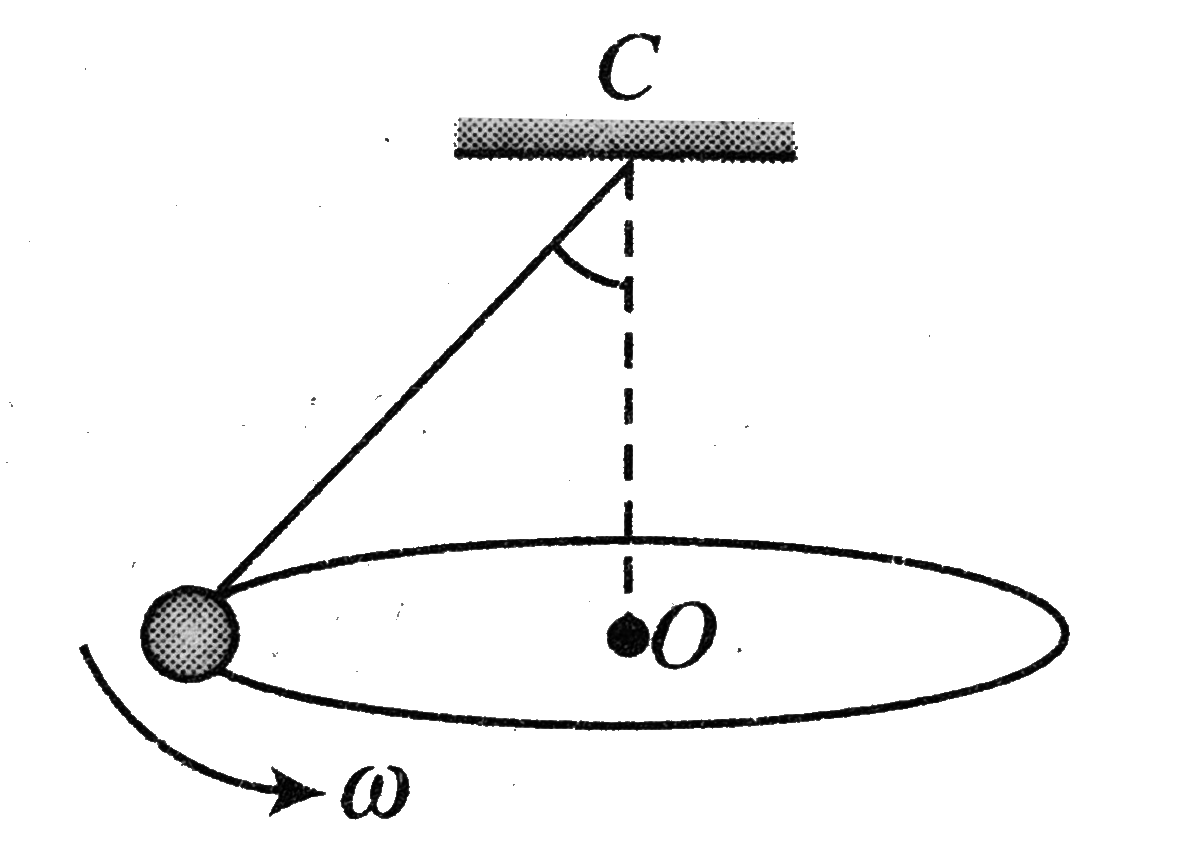
View SolutionFor' a body moving along the circumference of a circle with constant speed is constant
View Solution
