A stone of mass 1kg tied to a light inextensible sstring of length L=10m is whirling in a circular path of radius L in vertical plane. If the ratio of the maximum tension in the string to the minimmum tension in the string is 4 and if g is taken to be 10ms−2 , the speed of the stone at the highest point of the circle is.
5√2m/s
20m/s
10m/s
10√3m/s
The correct Answer is:C
Step by step video, text & image solution for A stone of mass 1kg tied to a light inextensible sstring of length L=10m is whirling in a circular path of radius L in vertical plane. If the ratio of the maximum tension in the string to the minimmum tension in the string is 4 and if g is taken to be 10ms^(-2) , the speed of the stone at the highest point of the circle is. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - TARGET PUBLICATIONCHAPTER - CIRCULAR MOTIONEXERCISE - COMPETITIVE THINKING102videos
CIRCULAR MOTION
- BOOK - TARGET PUBLICATIONCHAPTER - CIRCULAR MOTIONEXERCISE - EVALUATION TEST11videos
CIRCULAR MOTION
- BOOK - TARGET PUBLICATIONCHAPTER - CIRCULAR MOTIONEXERCISE - EVALUATION TEST11videos
CIRCULAR MOTION
- BOOK - TARGET PUBLICATIONCHAPTER - ATOMS, MOLECULES AND NUCLEI EXERCISE - Evaluation test19videos
ATOMS, MOLECULES AND NUCLEI
- BOOK - TARGET PUBLICATIONCHAPTER - CURRENT ELECTRICITY EXERCISE - Evaluation Test6videos
CURRENT ELECTRICITY
Similar Questions
A stone of mass m tied to a light inextensible sting of length L(=103m) is whirling in a circular path of radius L in a verticle plane. If the ratio of the maximum to the minimum tension is four, find the speed of the stone at the highest point of the circle.
View SolutionIf a stone of mass 2 kg is tied to a inextensible string of length 2 m is whirling in a circular path of radius L in vertical plane at uniform speed. If the ratio of maximum tension to minimum tension in the string is 3. Then, the speed of stone at highest point of circle is ...... m/s
View Solution
Knowledge Check
- Question 1 - Select One
A stone of mass 1 kg tied to a light inextensible string of lenth L=103m, whirling in a circular path in a vertical plane. The ratio of maximum tension to the minimum tension in the string is 4. If g is taken to be 10ms−2, the speed of the stone at the highest point of the circle is
A10ms−1B5√2ms−1C10√3ms−1D20ms−1 - Question 2 - Select One
A stone of 1 kg tied up with 10/3 m long string rotated in a vertical circle. If the ratio of maximum and minimum tension in string is 4 then speed of stone at highest point of circular path will be ( g=10ms2)
A20m/sB10√3m/sC5√2m/sD10m/s - Question 3 - Select One
A stone of mass 1 kg tied to a light inextensible string of length L=53m, is whirling in a vertical circle of radius L. If the ratio of the maximum and minimum tension in the string is 4 and g=10m/s2, the speed of stone at the highest point of the circle is
A5m/sB5√3m/sC5√2m/sD10m/s
Consider a stone of mass 1 kg tied to a light inextensible string and whirling in a vertical circular path. The length of the string is fount to be 104 m. It is also fount that theratio of the maximum to minimum tension is 3. The find the speed of the stone at the highest point of the circle in ms−1. (Take g=10ms−2)
View SolutionStone of mass 1kg is whirled in a circular path of radius 1 m. Find out the tension in the string if the linear velocity is 10 m/s ?
View SolutionA pendulum bob swings along a circular path on a smooth inclined plane as shown in figure, where m=3kg, l=0.75m, θ=37∘. At the lowest point of the circle the tension in the string is T=274N. Take g=10ms−2.
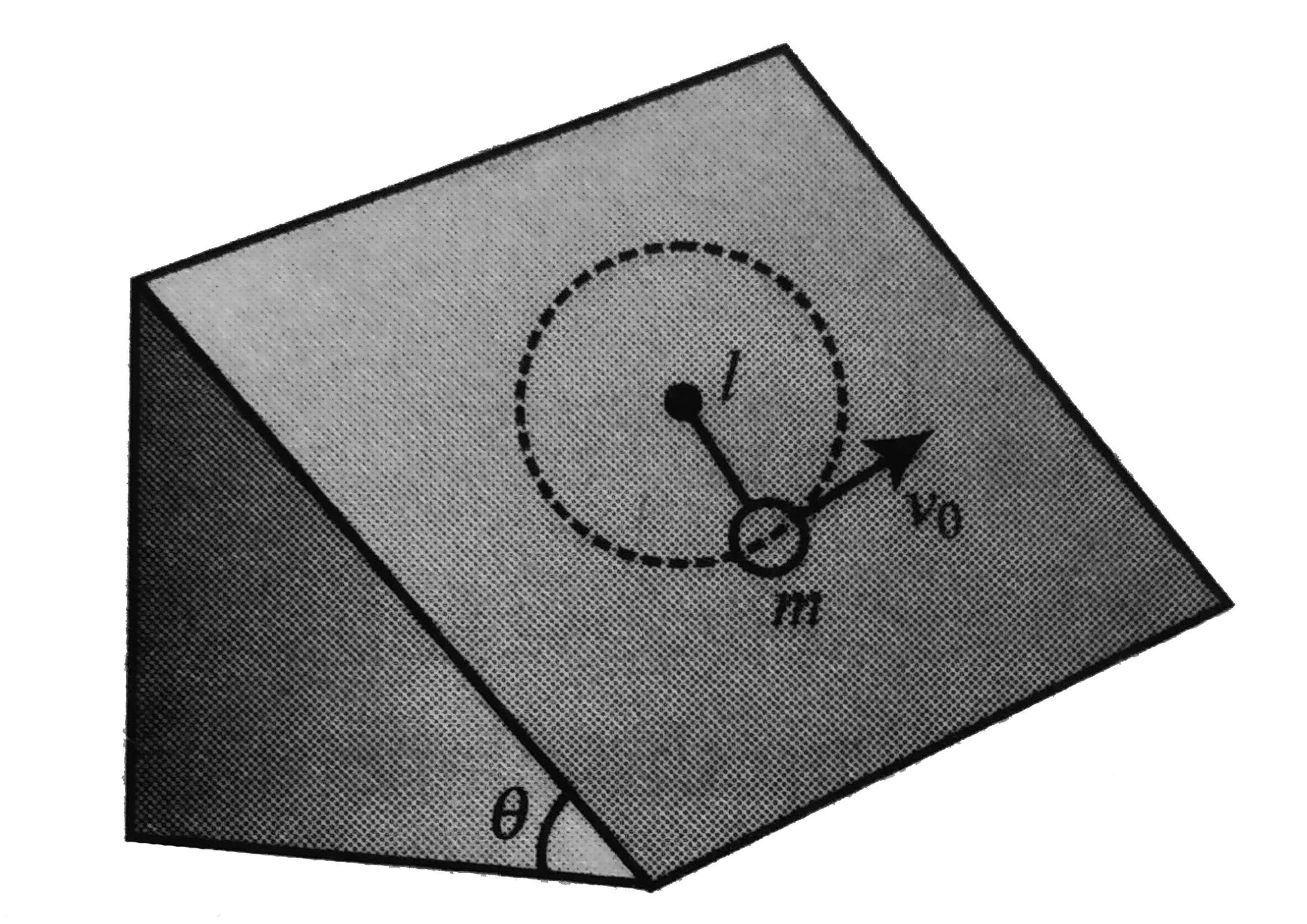
The speed of the bob at the highest point on the circle isView SolutionA stone of mass 5 kg is tied to a string of length 10 m is whirled round in a horizontal circle. What is the maximum speed with which the stone can be whirled around if the string can withstand a maximum tension of 200 N?
View SolutionA stone of mass 0.5 kg tied with a string of length 1 metre is moving in a circular path with a speed of 4 m/sec. The tension acting on the string in Newton is-
View Solution

