For many planets revolving around the stationary sun in circular orbits of different radii (R), the time periods (T) were noted. Then log(R) v/s log· (T) curve was plotted
[G=203×10−11 in M.K.S system, π2=10]
Estimate the mass of the sun.
![For many planets revolving around the stationary sun in circular orbits of different radii (R), the time periods (T) were noted. Then log(R) v/s log· (T) curve was plotted [G=(20)/3xx10^(-11) in M.K.S system, pi^2=10] Estimate the mass of the sun.](https://d10lpgp6xz60nq.cloudfront.net/physics_images/TRG_PHY_MCQ_XII_C02_E04_009_Q01.png)
6×1029kg
5×1020kg
8×1025kg
3×1025kg
The correct Answer is:A
Step by step video & image solution for For many planets revolving around the stationary sun in circular orbits of different radii (R), the time periods (T) were noted. Then log(R) v/s log· (T) curve was plotted [G=(20)/3xx10^(-11) in M.K.S system, pi^2=10] Estimate the mass of the sun. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - TARGET PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - COMPETITIVE THINKING109videos
GRAVITATION
- BOOK - TARGET PUBLICATIONCHAPTER - ELECTROSTATICSEXERCISE - EVALUATION TEST14videos
ELECTROSTATICS
- BOOK - TARGET PUBLICATIONCHAPTER - INTERFERENCE AND DIFFRACTIONEXERCISE - EVALUATION TEST20videos
INTERFERENCE AND DIFFRACTION
Similar Questions
For planets revolving round the sun, show that T2∝r3, where T is the time period of revolution of the planet and r is its distance from the sun.
View SolutionTwo stars of masses m1 and m2 form a binary system,revolving around each other in circular orbits of radii r1 and r2 respectively.Time period of revolution for this system is
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
If a planet of mass m is revolving around the sun in a circular orbit of radius r with time period, T then mass of the sun is
A4π2r3/GTB4π2r3/GT2C4π2r/GTD4π2r3/G2T2 - Question 2 - Select One
Many planets are revolving around the fixed sun in circular orbits of different radius (R) and difference time period (T) To estimate the mass of the sun the orbital radius (R) and time period (T) of planets were noted. Then log10 T v/s log10R curve was plotted.
The curve was found to be approximately straight line (as shown in) having y intercept =6.0 (Neglect the gravitational interaction among the planets) [Take G=203×10−11 in MKS, π2=10]
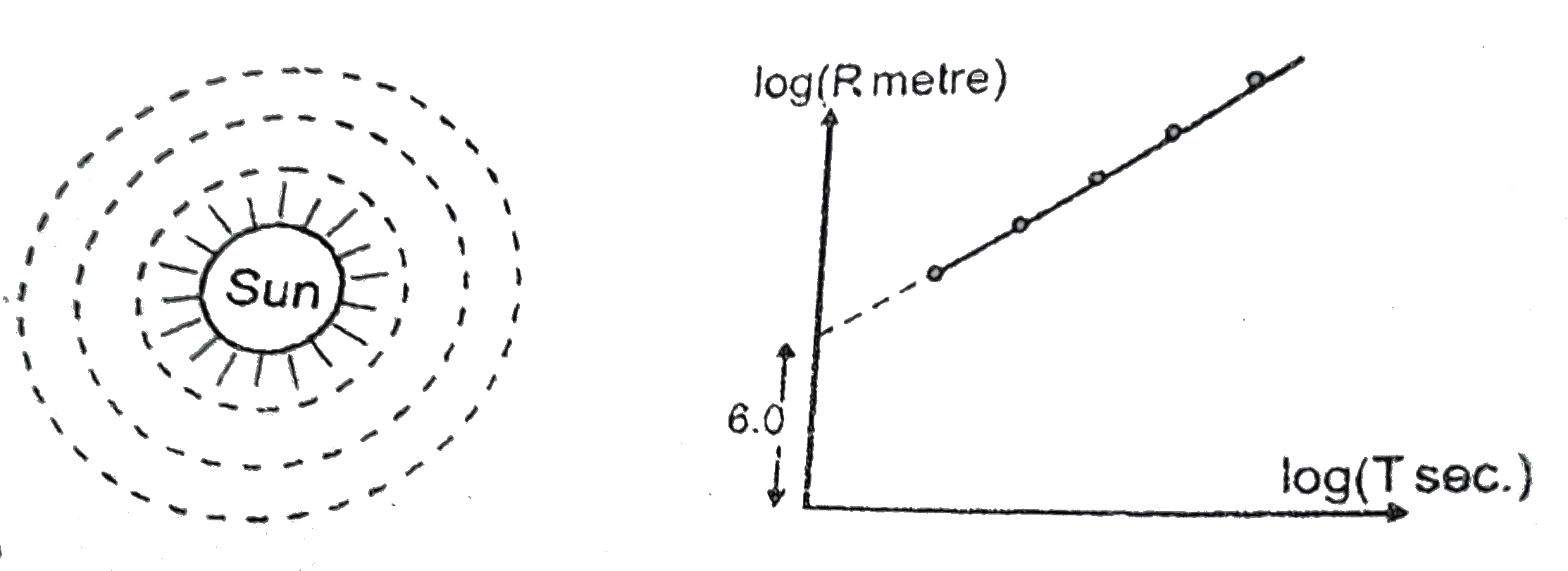
Estimate the mass of the sun .A6×1029kgB5×1020kgC8×1025kgD3×1035kg - Question 3 - Select One
Many planets are revolving around the fixed sun in circular orbits of different radius (R) and difference time period (T) To estimate the mass of the sun the orbital radius (R) and time period (T) of planets were noted. Then log10 T v/s log10R curve was plotted.
The curve was found to be approximately straight line (as shown in) having y intercept =6.0 (Neglect the gravitational interaction among the planets) [Take G=203×10−11 in MKS, π2=10]
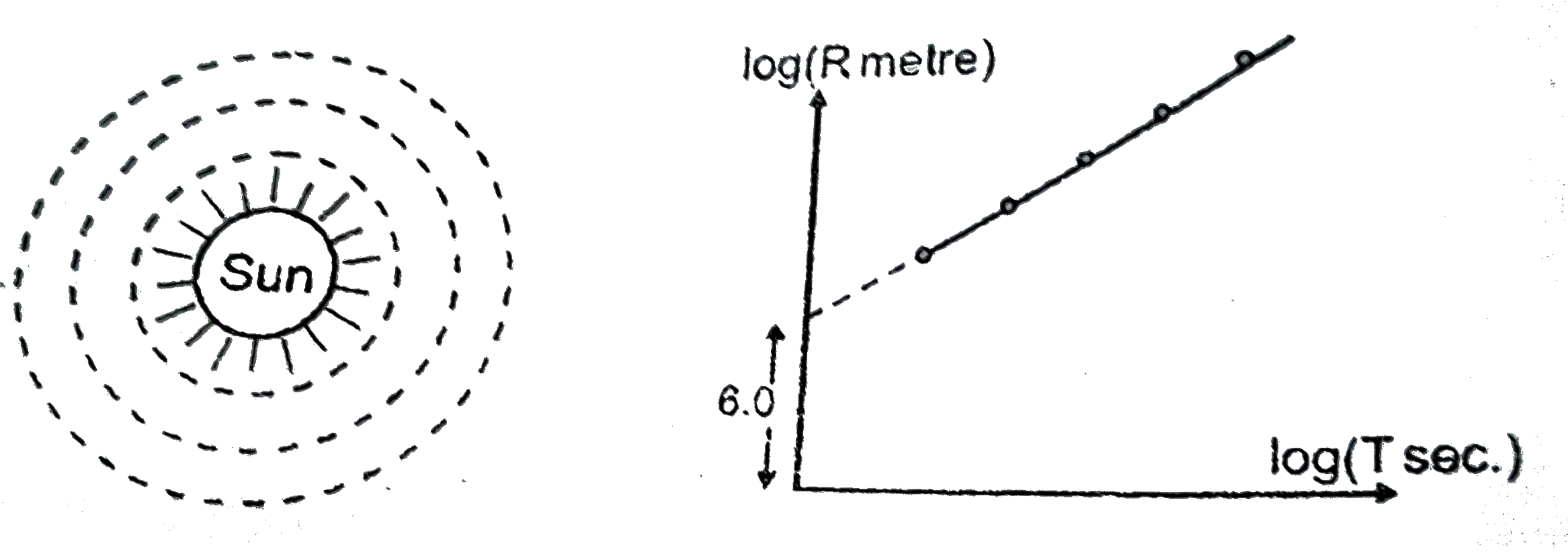
The slope of the line should be .A1B32C23D194
Suppose a light planet is revolving around a heavy star in a circular orbit of radius r and period of revolution T. The gravitational force of attraction between the star and the planet is proportional to 1r3/2. Derive the relation between T and r.
View SolutionMany planets are revolving around the fixed sun in circular orbits of different radius (R) and difference time period (T) To estimate the mass of the sun the orbital radius (R) and time period (T) of planets were noted. Then log10 T v/s log10R curve was plotted.
The curve was found to be approximately straight line (as shown in) having y intercept =6.0 (Neglect the gravitational interaction among the planets) [Take G=203×10−11 in MKS, π2=10]
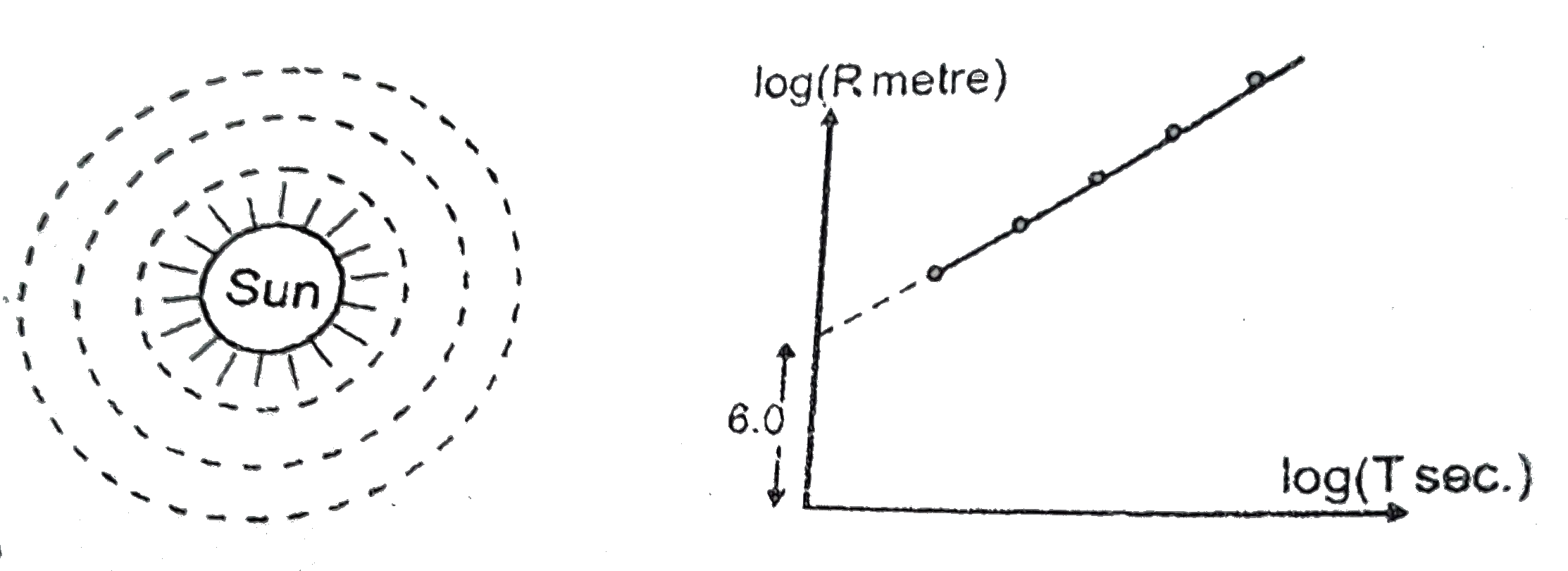
Two plantes A and B having orbital radius R and 4R are initally at the closest position and rotating in the same direction if angular velocity of planet B is ω0 then after how much time will both the planets be again in the closest postion? (Neglect the interaction between planets)
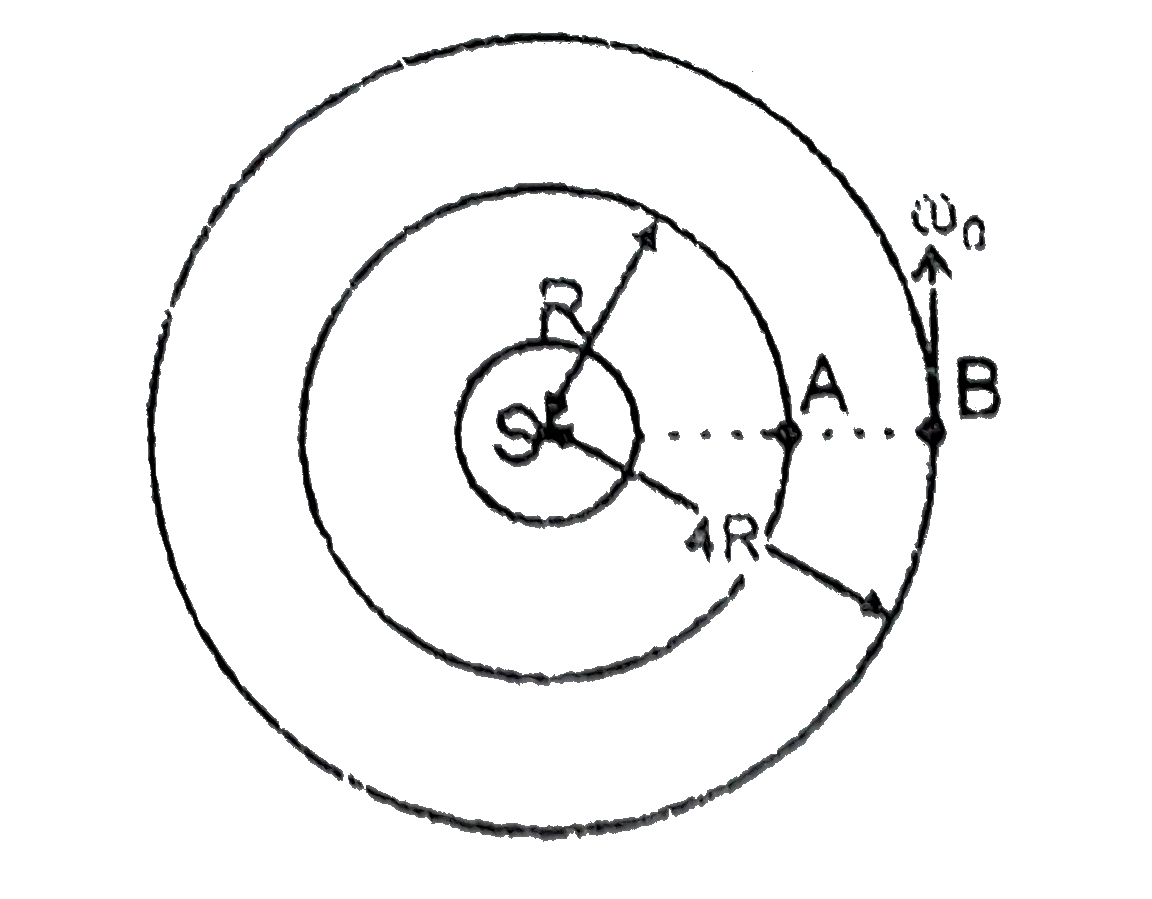 .View Solution
.View SolutionCharge q2 of mass m revolves around a stationary charge q1 in a circulare orbit of radius r. The orbital periodic time of q2 would be
View SolutionA planet is revolving around a star in a circular orbit of radius R with a period T. If the gravitational force between the planet and the star is proportional to R−3/2, then
View SolutionA planet is revolving around the sun in a circular orbit with a radius r. The time period is T .If the force between the planet and star is proportional to r−3/2 then the quare of time period is proportional to
View Solution

