A cylinder of mass M, radius R is kept on a rough horizontal plane at one extreme end of the platfonn at t = 0. Axis of the cylinder is parallel to z-axis. The platform is oscillating in the xy-plane and its displacement from origin is represented by x = 4 cos(2πt) metres. There is no slipping between the cylinder and the platfonn. Find the acceleration of the centre of mass of cylinder at t =16s
(##TRG_PHY_MCQ_XII_C04_E04_001_Q01.png" width="80%">
−53π2
−23π2
−83π2
−43π2
The correct Answer is:C
Step by step video, text & image solution for A cylinder of mass M, radius R is kept on a rough horizontal plane at one extreme end of the platfonn at t = 0. Axis of the cylinder is parallel to z-axis. The platform is oscillating in the xy-plane and its displacement from origin is represented by x = 4 cos(2pit) metres. There is no slipping between the cylinder and the platfonn. Find the acceleration of the centre of mass of cylinder at t =1/6s (##TRG_PHY_MCQ_XII_C04_E04_001_Q01.png" width="80%"> by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - TARGET PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - COMPETITIVE THINKING135videos
OSCILLATIONS
- BOOK - TARGET PUBLICATIONCHAPTER - MODEL QUESTION PAPER EXERCISE - MODEL QUESTION PAPER -II47videos
MODEL QUESTION PAPER
- BOOK - TARGET PUBLICATIONCHAPTER - QUESTION PAPER 2019EXERCISE - MCQ45videos
QUESTION PAPER 2019
Similar Questions
A cylinder of mass M and radius R is resting on a horizontal paltform (which is parallel to the x-y plane) with its exis fixed along the y-axis and free to rotate about its axis. The platform is given a motion in the x-direction given by x=Acos(ωt). There is no slipping between the cylinder and platform. The maximum torque acitng on the cylinder during its motion is ..................
View SolutionA cylinder of mass m and radius R is kept on a rough surface after giving its centre a horizontal speed v0. Find the speed of the centre of the cylinder when it stops slipping.
View Solution
Knowledge Check
- Question 1 - Select One
A uniform solid cylinder of mass 5kg and radius 0.1m is resting on a horizontal platform (parallel to the x-y plane) and is free to rotate about its axis along the y-axis the platform is given a motion in the x direction given by x=0.2 cos (10t) m if there is no slipping then maximum torque acting on the cylinder during its motion is
A0.2N−mB2.0N−mC5.0N−mD10.0N−m - Question 2 - Select One

A uniform solid cylinder of mass m and radius R is placed on a rough horizontal surface. A horizontal constant force F is applied at the top point P of the cylinder so that it start pure rolling. The acceleration of the cylinder isAF/3mB2F/3mC4F/3mD5F/3m - Question 3 - Select One or More
A solid cylinder of mass m and radius r is rolling on a rough inclined plane of inclination θ. The coefficient of friction between the cylinder and incline is μ. Then.
Africtional force is always μmgcosθBfriction is a dissipative forceCby decreasing θ, frictional force decreasesDfrictiona opposes translation and supports rotation.
A cylinder of mass m and radius R rolls down an inclined plane of inclination θ. Calculate the linear acceleration of the axis of cylinder.
View SolutionA cylinder of mass m and radius R rolls down an inclined plane of inclination θ. Calculate the linear acceleration of the axis of cylinder.
View SolutionA uniform plank of mass m, free to move in the horizontal direction only , is placed at the top of a solid cylinder of mass 2m and radius R. The plank is attached to a fixed wall by mean of a light spring constant k. There is no slipping between the cylinder and the plank , and between the cylinder and the ground. Find the time period of small oscillation of the system.
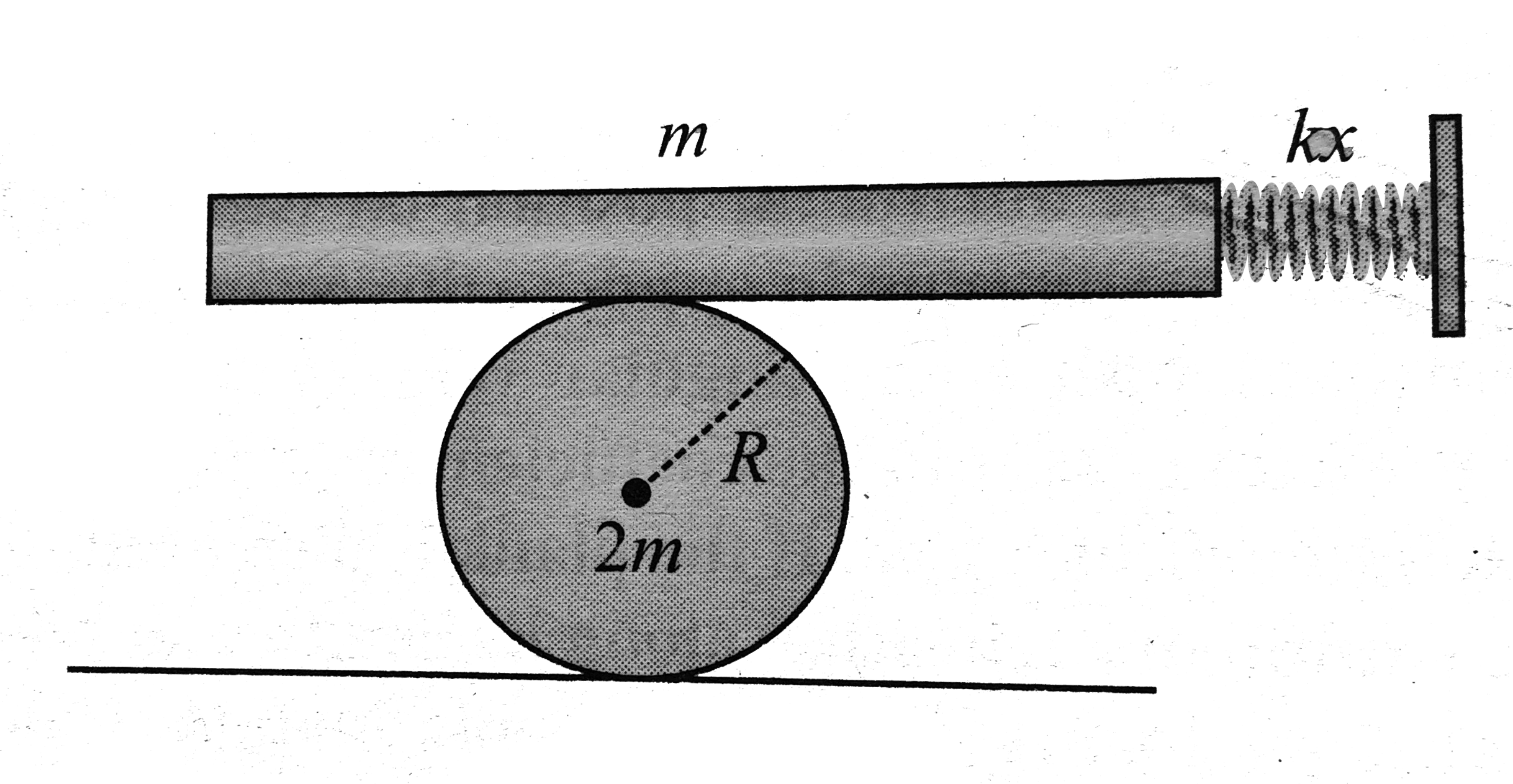 View Solution
View SolutionA solid cylinder of mass M and radius R rolls down an inclined plane of height h. The angular velocity of the cylinder when it reaches the bottom of the plane will be :
View SolutionA solid cylinder of mass M and radius R rolls from rest down a plane inclined at an angle θ to the horizontal. The velocity of the centre of mass of the cylinder after it has rolled down a distance d is :
View Solution

