A cyclotron in which flux density is 1.4 T is employed to accelerate protons. How rapidly should the field between the dees be reversed if mass of protoon be taken as 1.6×10−27 kg ?
4922×105 Hz
4922×107 Hz
4922×104 Hz
4922×106 Hz
The correct Answer is:B
To solve the problem of how rapidly the magnetic field in a cyclotron should be reversed to accelerate protons, we can follow these steps:
Step 1: Understand the relationship between frequency, charge, magnetic field, and mass
The frequency f of a charged particle moving in a magnetic field is given by the formula:
f=qB2πm
where:
- q is the charge of the proton,
- B is the magnetic flux density,
- m is the mass of the proton.
Step 2: Identify the values provided in the question
From the question, we have:
- Charge of the proton, q=1.6×10−19C
- Magnetic flux density, B=1.4T
- Mass of the proton, m=1.6×10−27kg
Step 3: Substitute the values into the frequency formula
Now, substituting the known values into the frequency formula:
f=(1.6×10−19C)×(1.4T)2π(1.6×10−27kg)
Step 4: Calculate the numerator
Calculating the numerator:
1.6×10−19×1.4=2.24×10−19C T
Step 5: Calculate the denominator
Calculating the denominator:
2π×1.6×10−27≈10.053×10−27kg
(using π≈3.14)
Step 6: Calculate the frequency
Now, substituting back into the frequency equation:
f=2.24×10−1910.053×10−27≈2.23×107Hz
Step 7: Conclusion
The frequency at which the magnetic field should be reversed is approximately:
f≈2.23×107Hz
The frequency f of a charged particle moving in a magnetic field is given by the formula:
f=qB2πm
where:
- q is the charge of the proton,
- B is the magnetic flux density,
- m is the mass of the proton.
From the question, we have:
- Charge of the proton, q=1.6×10−19C
- Magnetic flux density, B=1.4T
- Mass of the proton, m=1.6×10−27kg
Now, substituting the known values into the frequency formula:
f=(1.6×10−19C)×(1.4T)2π(1.6×10−27kg)
Calculating the numerator:
1.6×10−19×1.4=2.24×10−19C T
Calculating the denominator:
2π×1.6×10−27≈10.053×10−27kg
(using π≈3.14)
Now, substituting back into the frequency equation:
f=2.24×10−1910.053×10−27≈2.23×107Hz
The frequency at which the magnetic field should be reversed is approximately:
f≈2.23×107Hz
Topper's Solved these Questions
- MAGNETIC EFFECT OF ELECTRIC CURRENTBOOK - TARGET PUBLICATIONCHAPTER - MAGNETIC EFFECT OF ELECTRIC CURRENTEXERCISE - COMPETITIVE THINKING
111 Videos
- MAGNETIC EFFECT OF ELECTRIC CURRENTBOOK - TARGET PUBLICATIONCHAPTER - MAGNETIC EFFECT OF ELECTRIC CURRENTEXERCISE - EVALUATION TEST
19 Videos
- MAGNETIC EFFECT OF ELECTRIC CURRENTBOOK - TARGET PUBLICATIONCHAPTER - MAGNETIC EFFECT OF ELECTRIC CURRENTEXERCISE - EVALUATION TEST
19 Videos
- KINETIC THEORY OF GASES AND RADIATION BOOK - TARGET PUBLICATIONCHAPTER - KINETIC THEORY OF GASES AND RADIATION EXERCISE - Evaluation test
18 Videos
- MAGNETISMBOOK - TARGET PUBLICATIONCHAPTER - MAGNETISMEXERCISE - EVALUATION TEST
14 Videos
Similar Questions
In a cyclotron, a magnetic field of 2⋅4T is used to accelerate protons. How rapidly should the electric field between the dees be reversed? The mass and the charge of protons are 1⋅67×10−27kg and 1⋅6×10−19C respectively.
View SolutionIn cyclotron, magnetic field of 1.4 Wb/m2 is used. To accelerate protons, how rapidly should the electric field between the Dees be reversed?
(π=3.142,Mp=1.67×10−27kg,3=1.6×10−19C)
View Solution
Knowledge Check
An electron is projected with an initial speed v0=1.60×106ms−1 into the uniform field between the parallel plates as shown in fig. Assume that the field between the plates is uniform and directed vertically downward, and that the field outside the plates is zero. the electrons enters the field at a point midway between the plates. Mass of electron is 9.1×10−31kg.
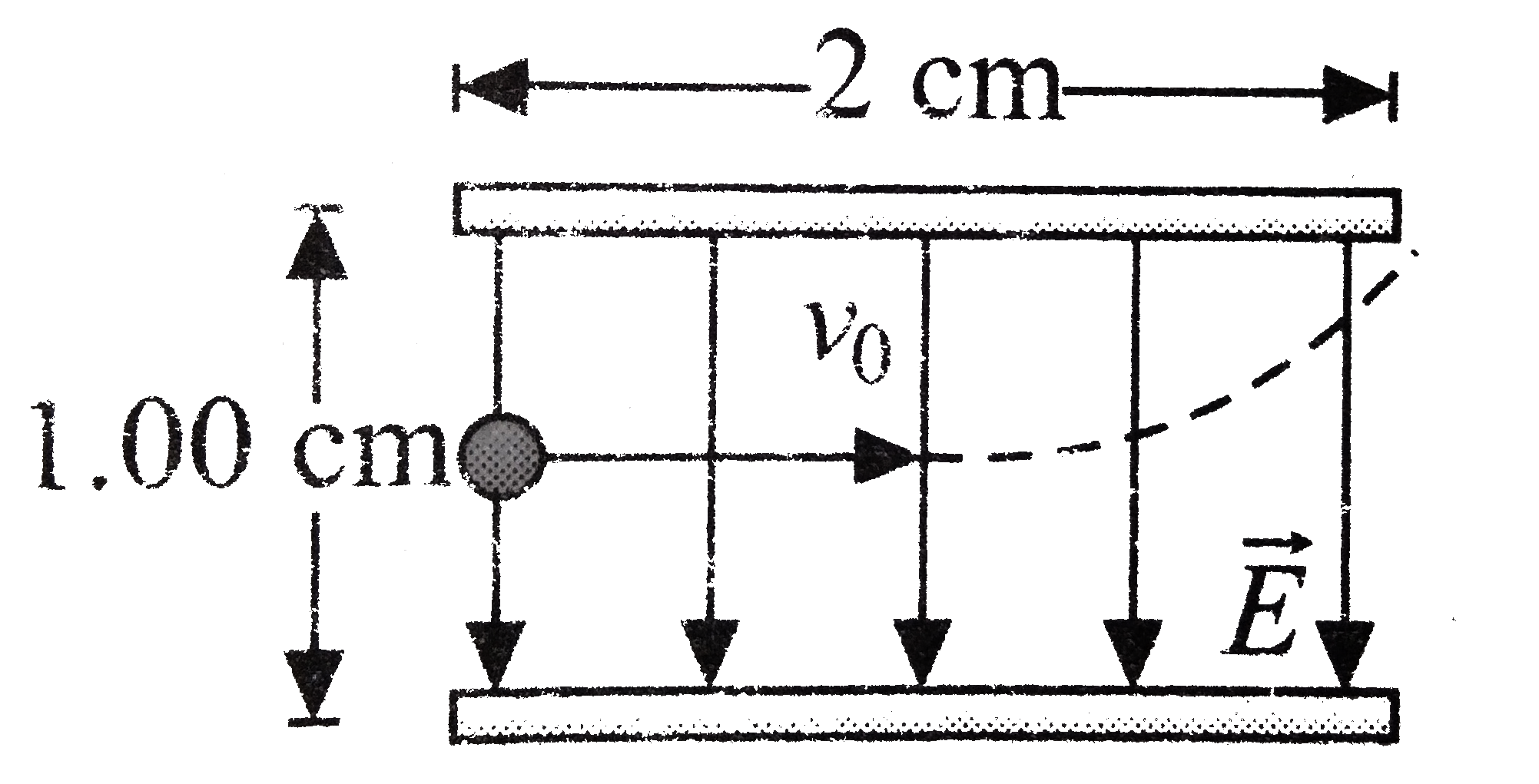
The vertical displacement traveled by the proton as it exits the region between the plated is (mass pf proton is 1.67×10−27kg).A1.6×10−8mB3.25×10−8mC5.25×10−6mD2.73×10−6mA 1.5m diameter cyclotron is used to accelerate proton to an energy of 8 MeV. The required magnetic field strength for this cyclotron is : -
(mp=1.6×10−27kg)A215TB415TC815TD1415T
In a cycloton, the protons are to be accelerated with a magnitude field of magnitude 1⋅5T. How rapidly should the electric field between the dees be reversed? Mass and charge of proton are 1⋅67×10−27kg and 1⋅6×10−19C respectively.
View SolutionFind the rest mass energy of a proton in MeV.
[mp=1.673×10−27kg]
View SolutionIn a cyclotron, a magnetic filed of 3.5Wb/m2 is used to accelerate protons. What should be the time interval in which the electric field between the dees should be reversed? [Mass of the proton =1.67×10−27kg, charge on the proton =1.6×10−19C]
View SolutionHow many protons weight 5kg? The mass of a proton is 1.67×10−27kg.
View SolutionThe radius of dees in a cyclotron is 1.9 m and the magnetic field applied on the cyclotron is 0.8 T. Calculate the energy gained by an emergent proton in cyclotron in keV. Mass of proton is 1.67×10−27 kg.
View SolutionFind the number of revolutions made by a proton in a cyclotron to attain one fourth of speed of light, if the maximum value of accelerating potential provided by the oscillator is 40 kV ? Take mass of the proton =1.67×10−27 kg .
View Solution
