Energy of the lowest level of hydrogen atom is −13.6eV. The energy of the photon emitted in the transition from n=3 to n=1 is
27 eV
9 eV
3 eV
12.09 eV
The correct Answer is:D
To find the energy of the photon emitted during the transition from n=3 to n=1 in a hydrogen atom, we can follow these steps:
Step 1: Understand the Energy Levels
The energy of an electron in the nth level of a hydrogen atom is given by the formula:
En=−13.6eVn2
where n is the principal quantum number.
Step 2: Calculate the Energy at n=3
Using the formula, we can calculate the energy of the electron at n=3:
E3=−13.6eV32
E3=−13.6eV9
E3=−1.51eV
Step 3: Calculate the Energy at n=1
Next, we calculate the energy of the electron at n=1:
E1=−13.6eV12
E1=−13.6eV
Step 4: Find the Energy of the Photon Emitted
The energy of the photon emitted during the transition from n=3 to n=1 is the difference in energy between these two levels:
Ephoton=E1−E3
Substituting the values we calculated:
Ephoton=(−13.6eV)−(−1.51eV)
Ephoton=−13.6eV+1.51eV
Ephoton=−12.09eV
Since energy is typically expressed as a positive value for emitted photons, we take the absolute value:
Ephoton=12.09eV
Final Answer
The energy of the photon emitted in the transition from n=3 to n=1 is 12.09eV.
---
The energy of an electron in the nth level of a hydrogen atom is given by the formula:
En=−13.6eVn2
where n is the principal quantum number.
Using the formula, we can calculate the energy of the electron at n=3:
E3=−13.6eV32
E3=−13.6eV9
E3=−1.51eV
Next, we calculate the energy of the electron at n=1:
E1=−13.6eV12
E1=−13.6eV
The energy of the photon emitted during the transition from n=3 to n=1 is the difference in energy between these two levels:
Ephoton=E1−E3
Substituting the values we calculated:
Ephoton=(−13.6eV)−(−1.51eV)
Ephoton=−13.6eV+1.51eV
Ephoton=−12.09eV
Ephoton=12.09eV
The energy of the photon emitted in the transition from n=3 to n=1 is 12.09eV.
Topper's Solved these Questions
- BOOK - TARGET PUBLICATIONCHAPTER - ATOMS, MOLECULES AND NUCLEI EXERCISE - Competitive Thinking180videos
ATOMS, MOLECULES AND NUCLEI
- BOOK - TARGET PUBLICATIONCHAPTER - ATOMS, MOLECULES AND NUCLEI EXERCISE - Evaluation test19videos
ATOMS, MOLECULES AND NUCLEI
- BOOK - TARGET PUBLICATIONCHAPTER - ATOMS, MOLECULES AND NUCLEI EXERCISE - Evaluation test19videos
ATOMS, MOLECULES AND NUCLEI
- BOOK - TARGET PUBLICATIONCHAPTER - CIRCULAR MOTIONEXERCISE - EVALUATION TEST11videos
CIRCULAR MOTION
Similar Questions
The ground state energy of an atom is −13.6eV. The photon emitted during the transition of electron from n=3 to n=1 state, is incidenet on a photosensitive material of unknown work function. The photoelectrons are emitted from the materials with a maximum kinetic energy of 9 eV. the threshold wavelength of the material used is
View SolutionThe ionization energy of the electron in the lowest orbit of hydrogen atom is 13.6 eV. The energies required in eV to remove an electron from three lowest energy orbits of hydrogen atom respectively are
View Solution
Knowledge Check
- Question 1 - Select One
The energy of the ground state of hydrogen atom is −13.6 eV. The energy of the photon emitted in the transiton from n=4 to n=2 is
A13.6 eVB2.55 eVC2.4 eVD1.66 eV - Question 2 - Select One
Energy of the lowest level of H-atom is -13.6 eV. The energy of the emitted photons in transition from fourth to second energy state is
A2.55 eVB3.2 eVC4.5 eVD5.4 eV - Question 3 - Select One
The ionization energy of the electron in the lowest orbit of hydrogen atom is 13.6 eV. The energies required in eV to remove an electron from three lowest energy orbits of hydrogen atom respectively are
A13.6,6.8,8.4B13.6,10.2,3.4C13.6,27.2,40.8D13.6,3.4,1.51
The energy levels of a hypotherical one electron atom are shown in figure
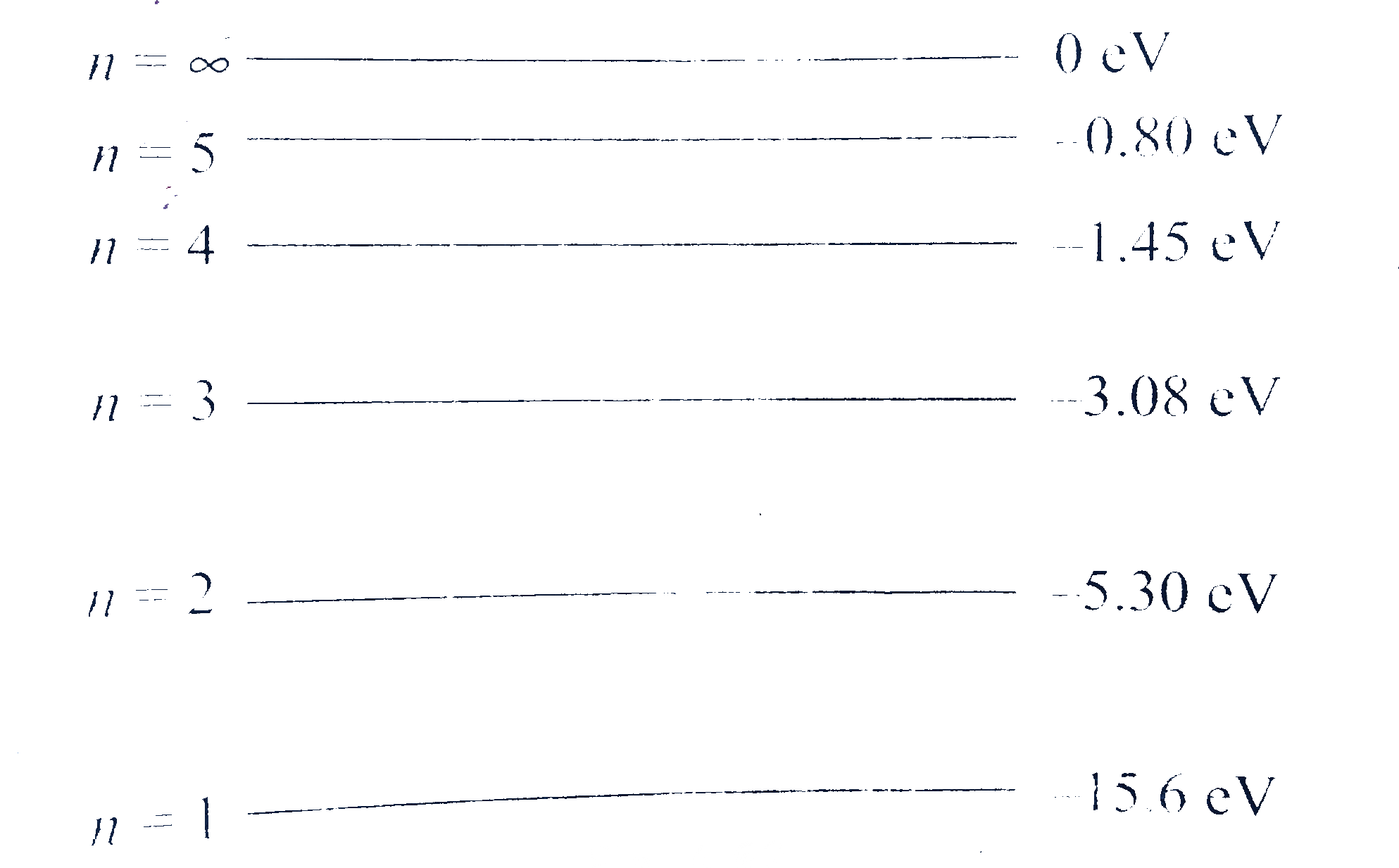
Find the wave number of the photon emitted for the transition n=3→n=1View SolutionThe ionisation energy of hydrogen is 13.6 eV . The energy of the photon released when an electron jumps from the first excited state (n=2) to the ground state of hydrogen atom is
View SolutionThe binding energy of e− in ground state of hydrogen atom is 13.6 eV . The energies required to eject out an electron from three lowest states of He+ atom will be (in eV):
View SolutionThe energy of hydrogen atom in its ground state is -13.6 eV , the energy of the level corresponding to n=7 is
View SolutionThe energy of a hydrogen atom in its ground state is −13.6eV. The energy of the level corresponding to the quantum number n=5 is
View Solution

