A body is projected vertically up from surface of the earth with a velocity half of escape velocity. The ratio of its maximum height of ascent and radius of earth is
The correct Answer is:C
To solve the problem, we need to find the ratio of the maximum height h attained by a body projected vertically upwards from the surface of the Earth with a velocity equal to half of the escape velocity, to the radius of the Earth R.
1. Understand Escape Velocity:
The escape velocity Ve from the surface of the Earth is given by the formula:
Ve=√2GMR
where G is the gravitational constant, M is the mass of the Earth, and R is the radius of the Earth.
2. Initial Velocity:
The body is projected with a velocity V1 which is half of the escape velocity:
V1=12Ve=12√2GMR=√GM2R
3. Conservation of Mechanical Energy:
The total mechanical energy at the surface (initial state) is equal to the total mechanical energy at the maximum height h (final state). The total energy consists of kinetic energy (KE) and potential energy (PE).
- At the Surface:
- Kinetic Energy (KE) at surface:
KE=12mv21=12m(√GM2R)2=12m⋅GM2R=mGM4R
- Potential Energy (PE) at surface:
PE=−GMmR
- Total Energy at surface:
Einitial=KE+PE=mGM4R−GMmR=mGM4R−4mGM4R=−3mGM4R
- At Maximum Height h:
- Kinetic Energy (KE) at maximum height:
KE=0(at maximum height, velocity is zero)
- Potential Energy (PE) at height h:
PE=−GMmR+h
- Total Energy at height h:
Efinal=0−GMmR+h=−GMmR+h
4. Setting Energies Equal:
From conservation of energy, we set the total energy at the surface equal to the total energy at height h:
−3mGM4R=−GMmR+h
5. Canceling Common Terms:
We can cancel −GMm from both sides (assuming m≠0):
34R=1R+h
6. Cross-Multiplying:
Cross-multiplying gives:
3(R+h)=4R
Simplifying this:
3R+3h=4R⟹3h=4R−3R⟹3h=R⟹h=R3
7. Finding the Ratio:
Now we find the ratio of maximum height h to the radius of the Earth R:
hR=R/3R=13
Final Answer:
The ratio of the maximum height of ascent to the radius of the Earth is:
hR=13
The escape velocity Ve from the surface of the Earth is given by the formula:
Ve=√2GMR
where G is the gravitational constant, M is the mass of the Earth, and R is the radius of the Earth.
The body is projected with a velocity V1 which is half of the escape velocity:
V1=12Ve=12√2GMR=√GM2R
The total mechanical energy at the surface (initial state) is equal to the total mechanical energy at the maximum height h (final state). The total energy consists of kinetic energy (KE) and potential energy (PE).
- Kinetic Energy (KE) at surface:
KE=12mv21=12m(√GM2R)2=12m⋅GM2R=mGM4R
- Potential Energy (PE) at surface:
PE=−GMmR
- Total Energy at surface:
Einitial=KE+PE=mGM4R−GMmR=mGM4R−4mGM4R=−3mGM4R
- Kinetic Energy (KE) at maximum height:
KE=0(at maximum height, velocity is zero)
- Potential Energy (PE) at height h:
PE=−GMmR+h
- Total Energy at height h:
Efinal=0−GMmR+h=−GMmR+h
From conservation of energy, we set the total energy at the surface equal to the total energy at height h:
−3mGM4R=−GMmR+h
We can cancel −GMm from both sides (assuming m≠0):
34R=1R+h
Cross-multiplying gives:
3(R+h)=4R
Simplifying this:
3R+3h=4R⟹3h=4R−3R⟹3h=R⟹h=R3
Now we find the ratio of maximum height h to the radius of the Earth R:
hR=R/3R=13
The ratio of the maximum height of ascent to the radius of the Earth is:
hR=13
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - LEVEL II (C.W.)38videos
GRAVITATION
- BOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - LEVEL III44videos
GRAVITATION
- BOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - C.U.Q220videos
GRAVITATION
- BOOK - NARAYNACHAPTER - FRICTIONEXERCISE - Passage type of questions I6videos
FRICTION
- BOOK - NARAYNACHAPTER - KINETIC THEORY OF GASESEXERCISE - LEVEL-III(C.W)52videos
KINETIC THEORY OF GASES
Similar Questions
A body is projected vertically upwards from the surface of the earth with a velocity equal to half of escape velocity of the earth. If R is radius of the earth, maximum height attained by the body from the surface of the earth is
View SolutionA body is projected vertically upwards from the surface of earth with a velocity equal to half the escape velocity. If R be the radius of earth, maximum height attained by the body from the surface of earth is Rn. Find the value of n.
View Solution
Knowledge Check
- Question 1 - Select One
A body is projected vertically upward from the surface of the earth, then the velocity-time graph is:-
A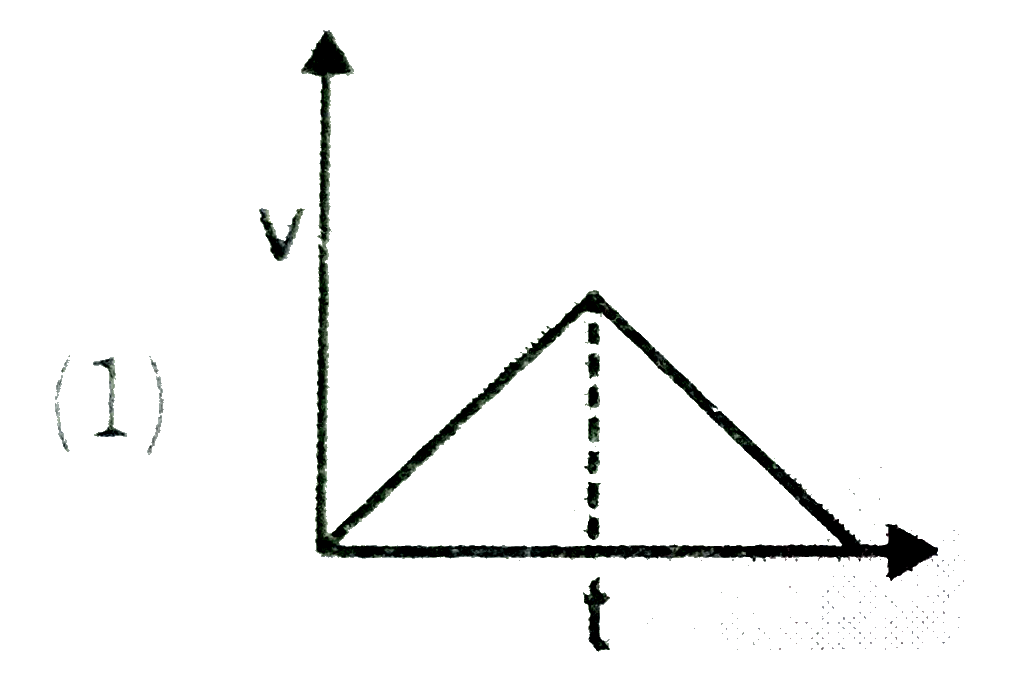 B
B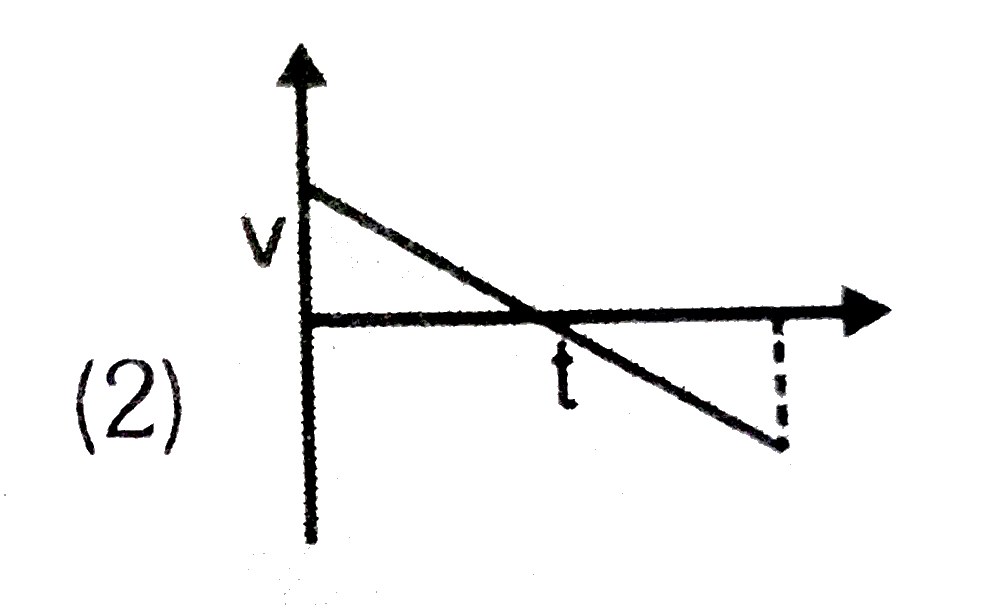 C
C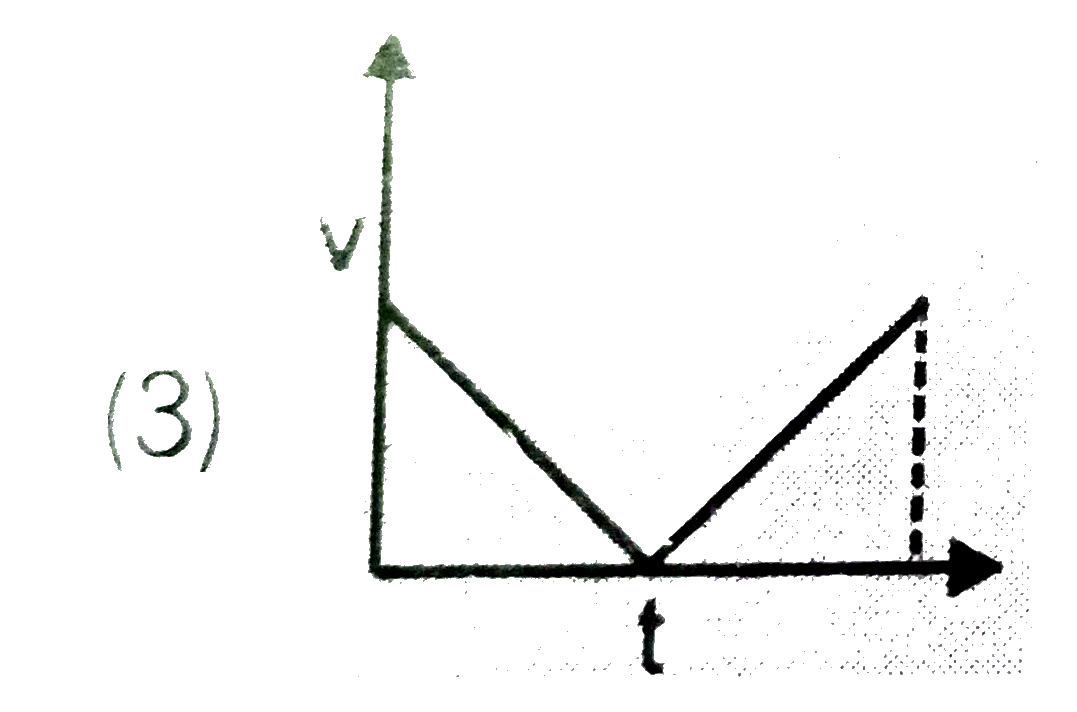 D
D
- Question 2 - Select One
An objects is projected vertically upwards from the surface of the earth with a velocity 3 times the escape velocity ve from earth's surface. What will be its final velocity after escape from the earth's gravitational pull ?
A√2veB2√2veC2veDve√2
A body is projected vertically upward from. the surface of the earth.with a velocity equal to half its escape velocity. If R is radius of the earth, then the maximum height attained by the,body is (Rn). Find n.
View SolutionAn object is projected vertically upward from the surface of the earth of mass M with a velocity such that the maximum height reached is eight times the radius R of the earth. Calculate:
(i) the initial speed of projection
(ii) the speed at half the maximum height.View SolutionA body is projected vertically upward from the surface of the earth with escape velocity. Calculate the time in which it will be at a height (measured from the surface of the arth) 8 time the radius of the earth (R). Acceleration due to gravity on the surface of the earth is g.
View SolutionA particle is projected vertically upwards the surface of the earth (radius Re) with a speed equal to one fourth of escape velocity what is the maximum height attained by it from the surface of the earth?
View SolutionA particle of mass m is projected upwards from the surface of the earth with a velocity equal to half the escape velocity. (R is radius of earth and M is mass of earth)Calculate the potential energy of the particle at its maximum. Write the kinetic energy of the particle when it was at half the maximum height.
View SolutionA particle is projected vertically upward the surface of the earth (radius Re ) with a speed equal to one-fourth of escape velocity. The maximum height attained by it from the surface of the earth is Rek. Find k.
View Solution

