Question

Three identical particles each of mass "m" are arranged at the corners of an equiliteral triangle of side "L". If they are to be in equilibrium, the speed with which they must revolve under the influence of one another's gravity in a circular orbit circumscribing the triangle is

Options

A. `sqrt((3Gm)/L)`
B. `sqrt((Gm)/L)`
C. `sqrt((Gm)/(3L))`
D. `sqrt((3Gm)/(L^(2)))`

Answer

B

Explanation

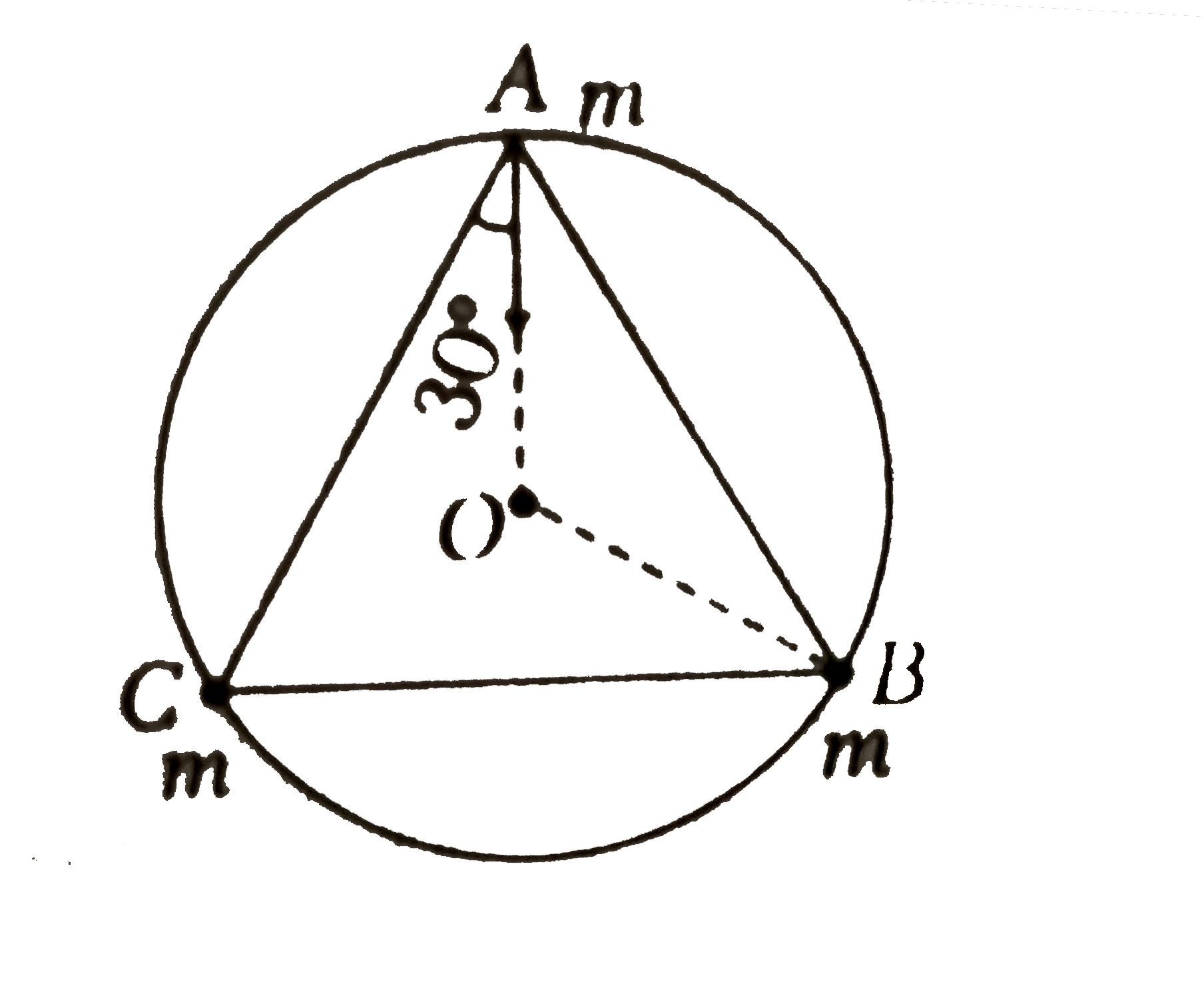
To solve the problem of three identical particles each of mass "m" arranged at the corners of an equilateral triangle of side "L" and determining the speed required for them to revolve in a circular orbit under the influence of each other's gravity, we can follow these steps:

Step 1: Understand the Forces Acting on Each Particle
Each particle experiences gravitational attraction from the other two particles. The gravitational force \( F \) between any two particles is given by Newton's law of gravitation:

\( F = \frac{G m^2}{L^2} \)

where \( G \) is the gravitational constant, \( m \) is the mass of each particle, and \( L \) is the distance between them.

Step 2: Calculate the Resultant Force on One Particle
For particle C, the forces acting on it due to particles A and B (denoted as \( F_{CA} \) and \( F_{CB} \)) can be resolved. Since the angle between the forces is \( 60^\circ \), we can find the resultant force \( F_R \) using vector addition:

\( F_R = \sqrt{F_{CA}^2 + F_{CB}^2 + 2 F_{CA} F_{CB} \cos(60^\circ)} \)

Since \( F_{CA} = F_{CB} = F \):

\( F_R = \sqrt{F^2 + F^2 + 2F^2 \cdot \frac{1}{2}} = \sqrt{3F^2} = \sqrt{3}F \)

Step 3: Determine the Radius of Circular Motion
The particles revolve around the centroid of the triangle. The distance from the centroid to any vertex (let's say point C) can be calculated. For an equilateral triangle, the distance from the centroid to a vertex is given by:

\( r = \frac{L}{\sqrt{3}} \)

Step 4: Apply Centripetal Force Condition
For the particles to remain in circular motion, the centripetal force must equal the resultant gravitational force acting on the particle. The centripetal force \( F_c \) is given by:

\( F_c = \frac{m v^2}{r} \)

Setting the centripetal force equal to the resultant gravitational force:

\( \frac{m v^2}{r} = \sqrt{3}F \)

Substituting \( F = \frac{G m^2}{L^2} \):

\( \frac{m v^2}{\frac{L}{\sqrt{3}}} = \sqrt{3} \cdot \frac{G m^2}{L^2} \)

Step 5: Solve for Velocity \( v \)
Rearranging the equation to solve for \( v^2 \):

\( m v^2 \cdot \frac{\sqrt{3}}{L} = \sqrt{3} \cdot \frac{G m^2}{L^2} \)

Cancelling \( m \) from both sides and simplifying:

\( v^2 = \frac{G m}{L} \)

Taking the square root gives:

\( v = \sqrt{\frac{G m}{L}} \)

Final Answer
The speed with which the particles must revolve in a circular orbit circumscribing the triangle is:

\( v = \sqrt{\frac{G m}{L}} \)