The velocity fo a body is expressed as V=GaMbRc where G is gravitational constant. M is mass, R is radius. The values of exponents a,b and c are:
12,12,−12
1,1,1
12,12,12
1,1,12
The correct Answer is:A
[LT−1]α[M−1L3T−2]aMbLc
Topper's Solved these Questions
- UNITS AND MEASUREMENTSBook:NARAYNAChapter:UNITS AND MEASUREMENTSExercise:LEVEL-III
Explore 21 Videos
- UNITS AND MEASUREMENTSBook:NARAYNAChapter:UNITS AND MEASUREMENTSExercise:Single Option Questions
Explore 12 Videos
- UNITS AND MEASUREMENTSBook:NARAYNAChapter:UNITS AND MEASUREMENTSExercise:LEVEL-I (C.W)
Explore 42 Videos
- TRANSMISSION OF HEATBook:NARAYNAChapter:TRANSMISSION OF HEATExercise:LEVEL-II(C.W)
Explore 27 Videos
- VECTORSBook:NARAYNAChapter:VECTORSExercise:LEVEL-II (H.W)
Explore 14 Videos
Similar Questions
Knowledge Check
If orbit velocity of planet is given by v=GaMbRc, then
Aa=13,b=13,c=−13Ba=13,b=12,c=−12Ca=12,b=−12,c=12Da=12,b=−12,c=−12If the orbital velocity of a planet is given by v=GaMbRc then
Aa=12,b=12,c=12Ba=12,b=12,c=−12Ca=12,b=−12,c=12Da=13,b=−13,c=−13The escape velocity of a sphere of mass m is given by (G= univesal gravitational constant, Me= mass of the earth and Re= radius of the earth)
A√GMeReB√2GMeReC√2GmReDGMeR2e
The escape velocity of a sphere of mass m is given by (G=Universal gravitational constant,M=Mass of the earth and Re=Radius of the earth)
View SolutionIf the energy, E=Gphqcr, where G is the universal gravitational constant, h is the Planck's constant and c is the velocity of light, then the values of p are q and r are, respectively
View SolutionIf the energy, E=Gphqcr, where G is the universal gravitational constant, h is the Planck's constant and c is the velocity of light, then the values of p, q and r are, respectively
View SolutionThe condition for a uniform spherical mass m of a radius r to be a black hole is [G =gravitational constant and g=acceleration due to gravity]
View SolutionThe condition for a uniform spherical mass m of a radius r to be a black hole is [G =gravitational constant and g=acceleration due to gravity]
View Solution

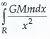 , where G,M and m are constants.
, where G,M and m are constants.