Two glass bulbs A and B are connected by a very small tube having a stop cock. Bulb A has a volume of 100 cm3 and contained the gas, while bulb B was empty. On opening th stop cock. The pressure fell down to 40%. The volume of the bulb B must be:
200
125
66
75
The correct Answer is:C
According to Boyle's law , at constant n and T , we have
pinitialVinitial=pfinalVfinal
pAVA=0.6pA(VA+VB)
pA(100)=0.6pA(100+VB)
100=0.6(100+VB)
166=100+VB
or VB=166−100=66
Topper's Solved these Questions
- STATES OF MATTERBOOK - R SHARMACHAPTER - STATES OF MATTEREXERCISE - Question Bank Level - IV
6 Videos
- STATES OF MATTERBOOK - R SHARMACHAPTER - STATES OF MATTEREXERCISE - ARCHIVES
41 Videos
- STATES OF MATTERBOOK - R SHARMACHAPTER - STATES OF MATTEREXERCISE - Question Bank Level - II
15 Videos
- SOME BASIC CONCEPTS OF CHEMISTRYBOOK - R SHARMACHAPTER - SOME BASIC CONCEPTS OF CHEMISTRYEXERCISE - Archives
26 Videos
- STRUCTURE OF ATOMBOOK - R SHARMACHAPTER - STRUCTURE OF ATOMEXERCISE - ARCHIVES
55 Videos
Similar Questions
Two cylinders A and B of equal capacity are connected to each other vis a stop cock. A contains an ideal gas at standard temperature and pressure. B is completely evacuated. The sto cock is suddenly opened. The process is:
View SolutionInitially bulb "a" contained oxygen gas at 27∘C and 950 mm of Hg and bulb "B" contained neon gas at 27∘C and 900 mm of Hg. These bulbs are connected by a narrow tube of negligible volume equipped with a stopcock and gases were allowed to mix-up freely. The pressure obtained in the combined system was found to be 910 mm of Hg.
If volume of bulb B was measured to be 10 L, then find the volume of oxygen gas present initially in bulb "A" .
View Solution
Knowledge Check
Two glass bulbs x and y are connected by a very small tube having a stop - cock. Bulb X has a volume of 100cm3 and contained the gas, while bulb Y was empty. On opening the stop - cock, the pressure fell down to 60%. The volume of the bulb Y must be
A132.32cm3B124cm3C66.66cm3D150cm3Two glass bulbs A and B are connected by very small tube having a stop cock. Bulb A has a volume of 100 ml and contained the gas while bulb B was empty and had a volume of 150 ml. on opening the stop-cock, the pressure of the gas in bulb A will fall down to:
A0.8B0.6C0.4D0.2Two glass bulbs A and B are connected by a very small tube having a stop cock. Bulb A has a volume of 100 cm3 and contained the gas, while bulb B was empty. On opening th stop cock. The pressure fell down to 40%. The volume of the bulb B must be:
A200B125C66D75
Two glass bulbs of equal volume and filled with an ideal gas at 500 K and pressure of 76 cm of Hg are connected by a norrow tube.One of the bulb is then placed in a water bath maintained at 700 K and the other bulb is maintained at 500 K.What is the new value of the pressure (in cm of Hg) inside the bulbs ? The volume of the connecting tube is negligible.Report your answer after multiplying by 67.
View SolutionTwo identical glass bulbs are interconnected by a thin tube of negligible volume. An ideal gas is filled in the bulbs at STP. One bulb is placed in a tub of melting ice and the other bulb is placed in a hot bath. The gas pressure in the bulbs becomes 1.5 times. Find the tem perature of the hot bath. Which bulb has more gas?
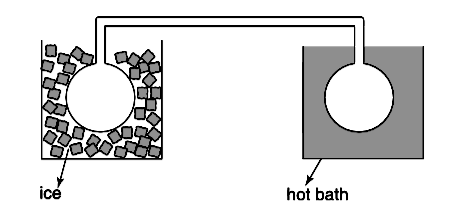View SolutionTwo identical glass bulbs, connected by a thin glass tube, are filled with He gas at S.T.P one of the bulbs is placed in a vessel containign ice while other is placed in a hot bath. The pressure of the gas increases to 1.5 times the initial pressure. If the temperature of a hot bath is 10t∘C. Find the value of t.
View SolutionTwo gases bulbs A and B are connected by a tube having a stopcock. Bulb A has a volume of 100mL and contains H2 gas . After opening the gas from A to the evacuated bulb B , the pressure falls down by 40%. The volume (mL)ofB must be
View SolutionTwo gas bulbs are connected by a thin tube. Calaculate the partial pressure of helium after the connective value is opened at a constant temperature of 27∘C
View Solution