Which of the following types of octahedral complexes can show mer-fac isomerism ?
where M is central metal, A, B and c are different monodentate ligands while AA is a symmetrical bidentate ligand.

A

$M A_{4} B_{2}$ or $M A_{2} B_{4}$

B

$M {(A A)}_{2} B_{2}$ or $M {(A A)}_{2} B C$

C

$M A_{3} B_{3}$

D

$M A_{5} B$

Text Solution

Verified by Experts

The correct Answer is:C

Two diastereoisomers are possible for an octahedral complex of the type $M A_{4} B_{2}$

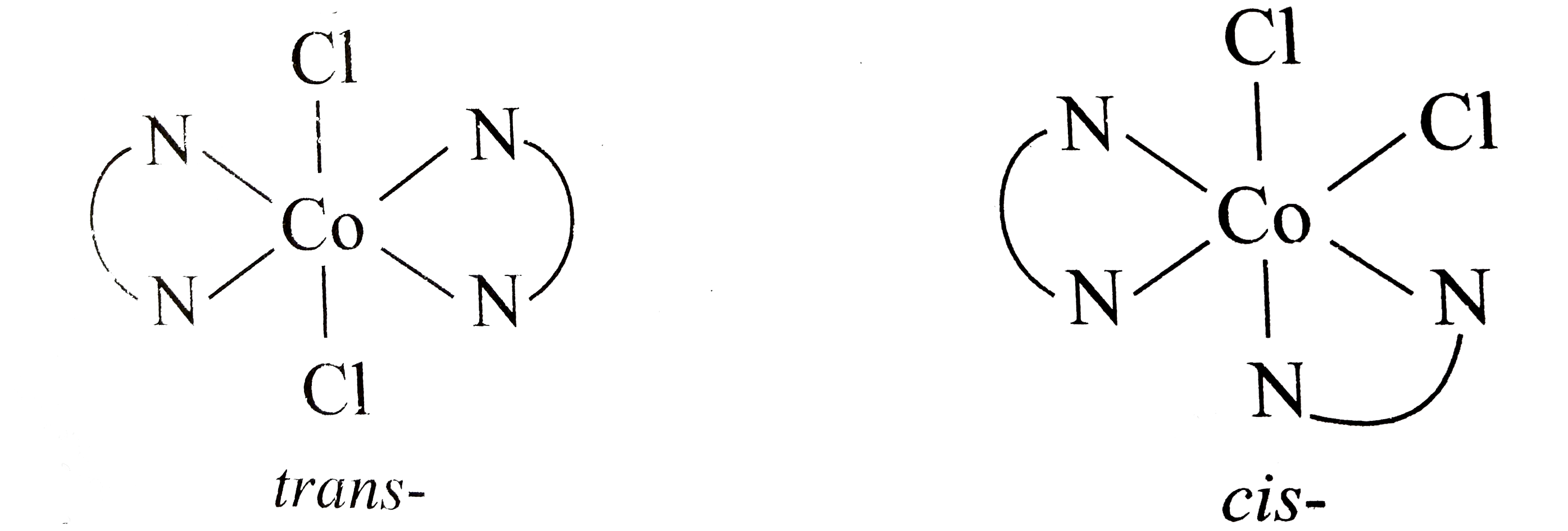
Note that two of the A ligands occupy positions just opposite one another. The four ligands have a square planar arrangement in which cis-trans isomers are possible. Two diastereoisomers are also possible for an octachedral complex of the type $M {(A A)}_{2} B_{2}$ or $M {(A A)}_{2} B C$ as illustrated in Q.2. Octahedral complexes with the general formula $M A_{3} B_{3}$ exhibit mer-fac isomerism. If we first draw an A ligand and a B ligand opposite one another in an octahedral geometry. Then the other ligands can have cis or trans arrangements on the plane perpendicular toi the axis of the first A and B ligands:

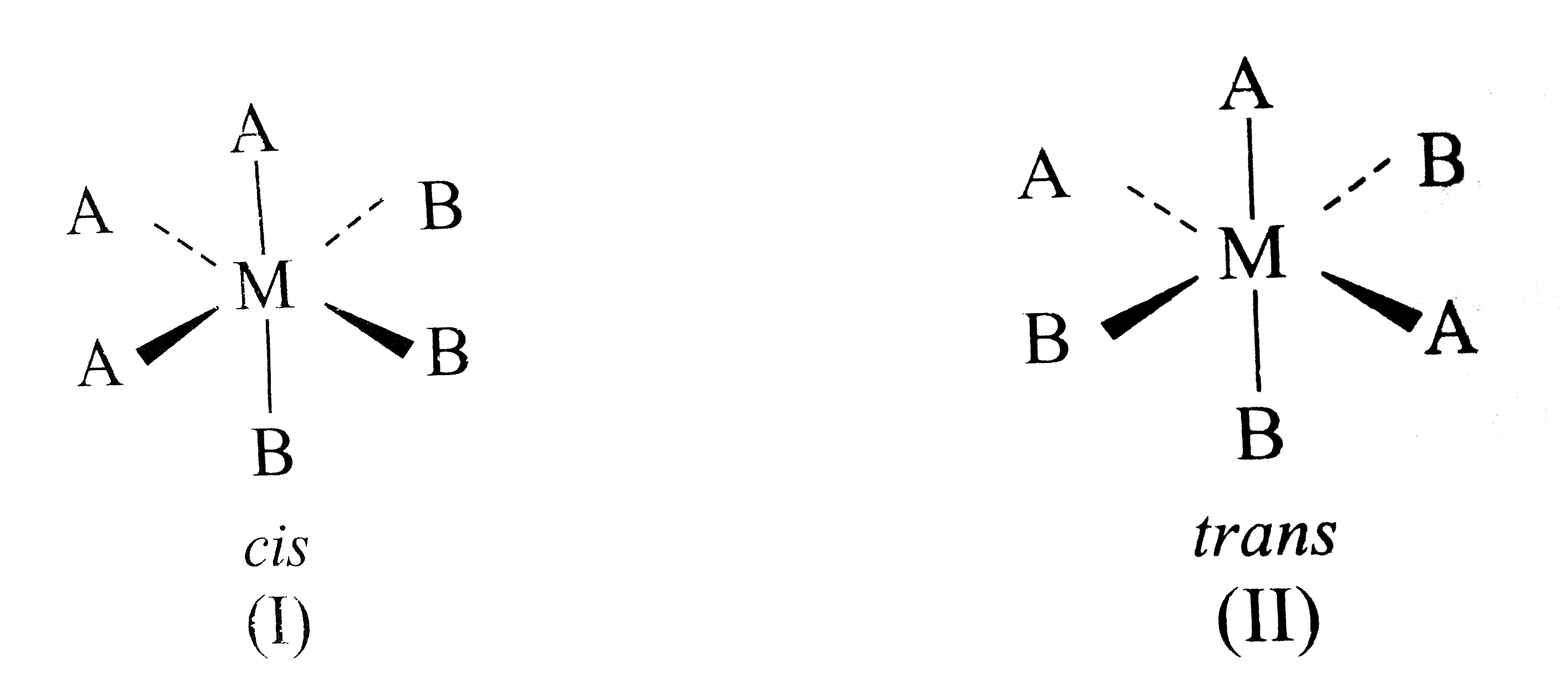
Isomer (I) show above has the three A ligands in adjacent positions ( $90^{\circ}$ separation) on one triangular face of the octahedron (fac-isomer), isomer (II) has all three A ligands in a plane that contains the M (mer-isomer). In isomer (I), all three B-M-B bonds angles are $90^{\circ}$ whereas in isomer (II) two B-M-B angles are $90^{\circ}$ and the third is $180^{\circ}$ . To convince ourselves that only two diasterosiomers of $M A_{3} B_{3}$ exist, look back at the cis-and trans- $[M A_{4} B_{2}]$ and consoider the products obtained form them when one of the four A ligands in cis-isomer is replaced by a B. There are two kinds of A-ligands in the cis-isomer: two A ligands that are trans to each other and two A ligands that are trans to a B ligands. Replacing an A trans to another A with B gives $[M A_{3} B_{3}]$ isomer (I), whereas replacing an A trans to a B with another B gives isomer (II)

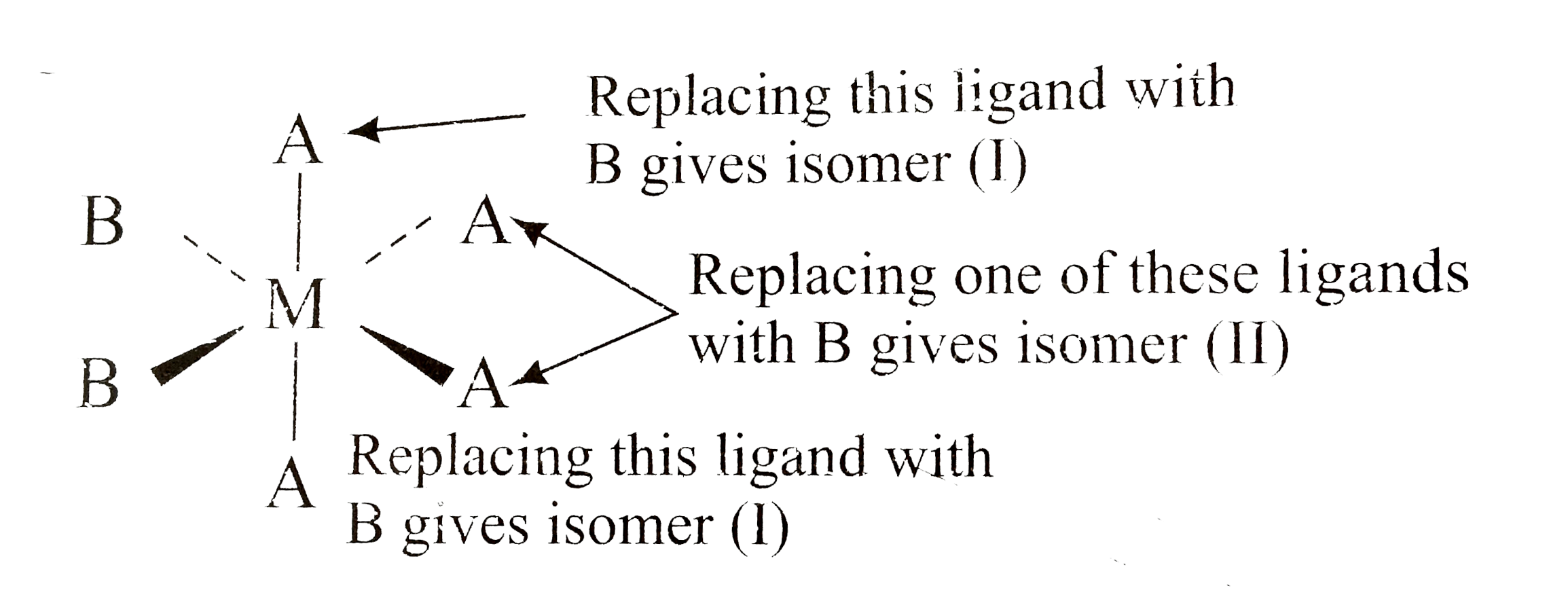
All four A ligands in trans - $[M A_{4} B_{2}]$ are equivalent, and replacing any one of them with a B gives isomer (II).

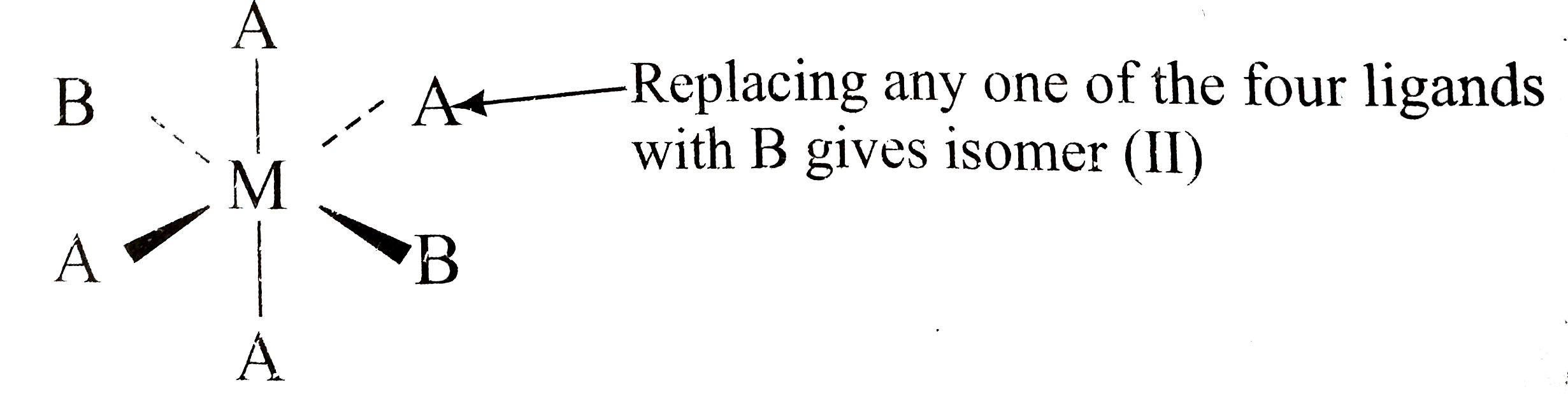
If we rotate the resulting $[M A_{3} B_{3}]$ complex, we can see that it is identical to the previous drawing of isomer (II). Thus, there are only two diasteroisomers for a complex of the type $[M A_{3} B_{3}]$ . Octahedral complexes of the type $[M A_{6}]$ or $[M A_{5} B]$ would not show geometrical isomerism.

Updated on:21/07/2023

|

Class 12 CHEMISTRY COORDINATION COMPOUNDS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Which of the following types of octahedral complexes does not show optical isomerism ?
A $M {(a a)}_{2} x y$
B $[M {(a a)}_{3}]$
C ${[M {(a a)}_{2} x_{2}]}_{2}^{n +}$
D $[M a_{5} b]$
Which of the following types of octahedral complexes does not show optical isomerism ?
A $M A_{2} X_{2} Y_{2}$
B ${[M {(A A)}_{3}]}_{3}^{n +}$
C ${[M {(A A)}_{2} X_{2}]}_{2}^{n +}$
D ${[P t {(N H)}_{3})}_{4}]^{2 +}$
Which of the following types of octahedral complexes does not show optical isomerism?
A(a) $M A_{2} X_{2} Y_{2}$
B(b) ${[P t {(N H)}_{3})}_{4}]^{2 +}$
C(c) ${[M {(A A)}_{3}]}_{3}^{n +}$
D(d) ${[M {(A A)}_{2} X_{2}]}_{2}^{n +}$

R SHARMA-COORDINATION COMPOUNDS-Archives

Home
Ask Doubt
Profile