A particle moves in the x−y plane such that its coordinates are given x=10√3t,y=10t−t2 and t is time, find the initial velocity of the particle.
x=10√3t
vx=dxdt=10√3
y=10t−t2
vy=dydt=10−2t
At t=0,vx=10√3m/s
vy=10−2t=10−2×0=10m/s
Initial velocity v=√v2x+v2y=20m/s
tanθ=vyvx=1010√3=1√3⇒θ=30∘
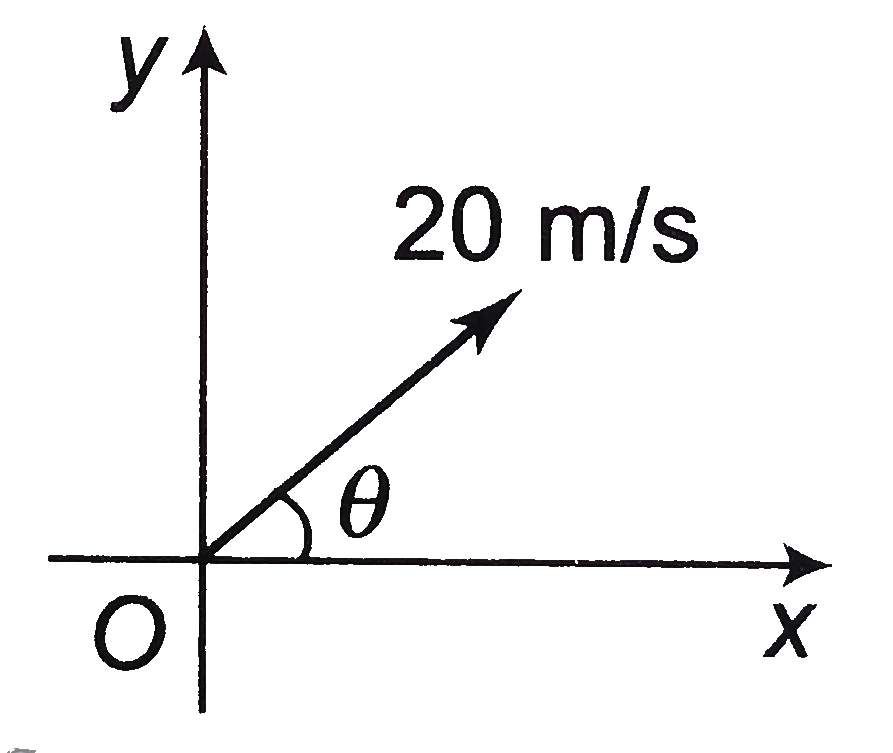
Topper's Solved these Questions
Similar Questions
(a) A particle starts moving at t=0 in x−y plane such that its coordinates (in cm) with time (in sec) change as x=3t and y=4sin(3t). Draw the path of the particle.
(b) If position vector of a particle is given by →r=(4t2−16t)ˆi+(3t2−12t)ˆj, then find distance travelled in first 4 sec.View SolutionA particle moves in an XY-plane in such a way that its x and y-coordinates vary with time according to
x(t)=t3−32t,y(t)=5t2+12
Find the acceleration of the particle, if t = 3 s.View Solution
Knowledge Check
- Question 1 - Select One
A particle moves in a plane such that its coordinates changes with time as x=at and y=bt, where a and b are constants. Find the position vector of the particle and its direction at any time t.
A(a)ˆi+(bt)ˆjB(at)ˆi+(b)ˆjC(at)ˆi+(bt)ˆjD(a)ˆi+(b)ˆj - Question 2 - Select One
A particle moves along X-axis in such a way that its coordinate X varies with time t according to the equation x=(2−5t+6t2)m. The initial velocity of the particle is
A−5m/sB6m/sC−3m/sD3m/s - Question 3 - Select One
A particle moves along x-axis in such a way that its r-coordinate varies with time't according to the equation x= (8−4t+6t2) metre. The velocity of the particle will vary with time according to the graph
A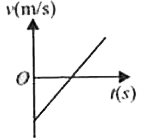 B
B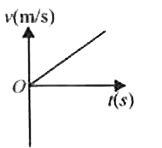 C
C D
D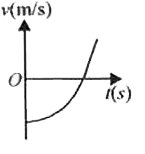
A particle moves along x axis in such a way that its coordinate x varies with time t according to the equation x=A0−A1t+A2t2. The initial velocity of the particle is.
View SolutionA particle moves along x-axis in such a way that its x-coordinate varies with time t according to the equation x=(8−4t+6t2) metre.
The velocity of the particle will vary with time according to the graph :-View SolutionA particle moves in the x-y plane. It x and y coordinates vary with time t according to equations x=t2+2t and y=2t. Possible shape of path followed by the particle is
View SolutionA particle moves along x-axis and its acceleration at any time t is a = 2 sin (πt), where t is in seconds and a is in m/s2 . The initial velocity of particle (at time t = 0) is u = 0.
Q. Then the magnitude of displacement (in meters) by the particle from time t = 0 to t = t will be :View SolutionA particle moves along x-axis and its acceleration at any time t is a = 2 sin (πt), where t is in seconds and a is in m/s2 . The initial velocity of particle (at time t = 0) is u = 0.
Q. Then the distance travelled (in meters) by the particle from time t = 0 to t = t will be :View Solution

