A particle is moving in a plane with velocity $\to v = u_{0} ˆ i + k ω cos ω t ˆ j$ . If the particle is at origin at $t = 0$ , (a) determine the trajectory of the particle. (b) Find its distance from the origin at $t = 3 π / 2 ω$ .

Video Solution

Text Solution

Verified by Experts

(a) $\to v = u_{0} ˆ i + k ω cos ω t ˆ j = v_{x} ˆ i + v_{y} ˆ j$ $v_{x} = u_{0}$
$\frac{d x}{d t} = u_{0} \Rightarrow \int_{0}^{x} d x = u_{0} \int_{0}^{t} d t$
$x = u_{0} t$ (i)
$\Rightarrow t = \frac{x}{u_{0}}$
$v_{y} = k ω cos ω t$
$\frac{d y}{d t} = k ω cos ω t \Rightarrow \int_{0}^{y} d y = k ω \int_{0}^{t} cos ω t d t$
$y = k ω {∣ ∣ ∣ \frac{sin ω t}{ω} ∣ ∣ ∣}_{0}^{t} = k sin ω t$ (ii)
Eliminating $t$ from (i) and (ii), we get
$y = k sin ω t = k sin (\frac{ω t}{u_{0}})$
$= k sin (\frac{ω x}{u_{0}}) [sine curve]$
If $\frac{ω x}{u_{0}} = \frac{π}{2} \Rightarrow x = \frac{π u_{0}}{2 ω}, y = k$
$\frac{ω x}{u_{0}} = π \Rightarrow \frac{π u_{0}}{ω}, y = 0$

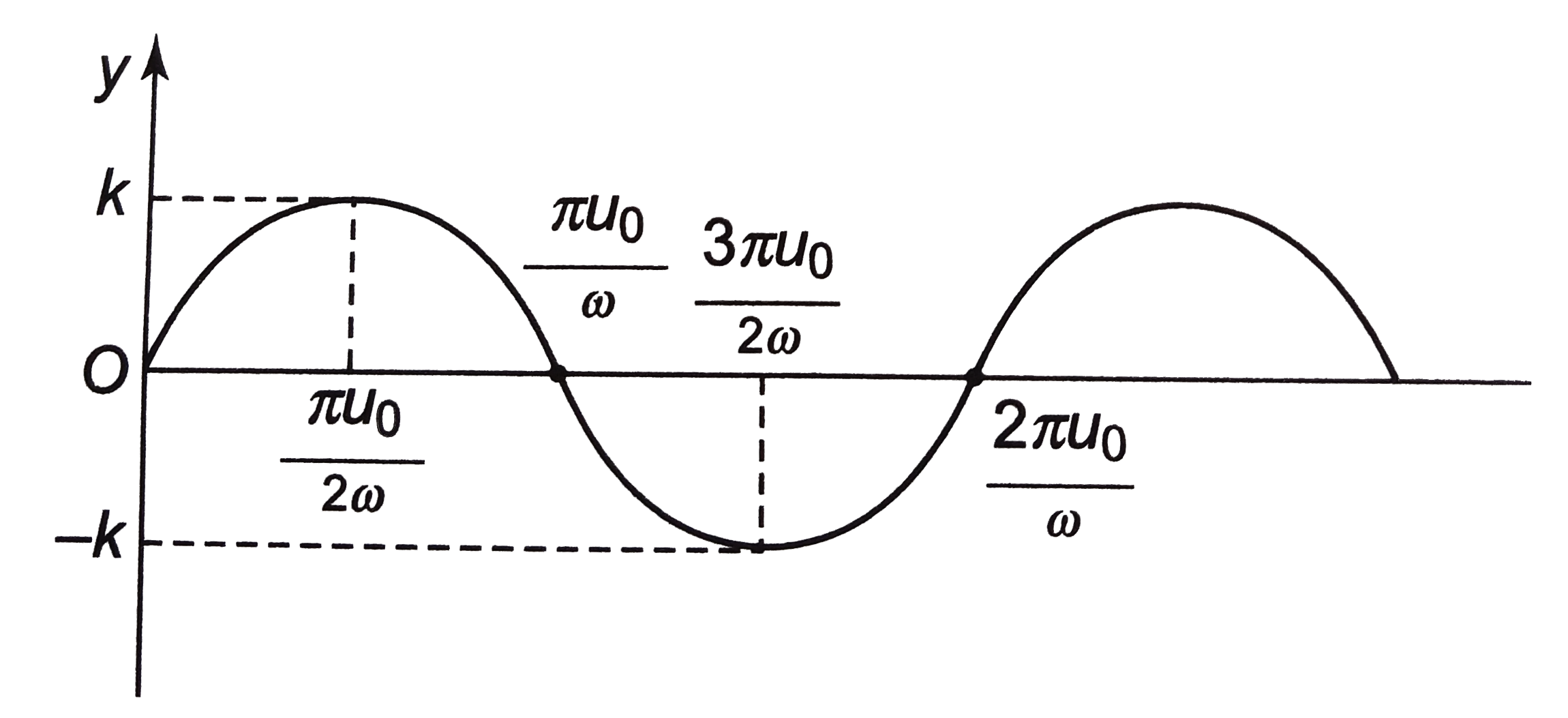
At $t = \frac{3 π}{2 ω}, x = u_{0} t = \frac{3 π u_{0}}{2 ω}$
$y = k sin (\frac{ω . 3 π}{2 ω}) = - k$
$r = \sqrt{x^{2} + y^{2}} = \sqrt{{(\frac{3 π u_{0}}{2 ω})}^{2} + k^{2}}$
where $r$ is the distance from the origin.

Updated on:21/07/2023

A particle moves in the xy plane according to the equation
$\to r = (ˆ i + 2 ˆ j) A cos ω t$
The motion of the particle is
Aon a straight line
Bin an ellipse
Cperiodic
Dsimple harmonic.
A particle moves in x-y plane according to the equation $¯ r = (ˆ i + 2 ˆ j) A cos ω t$ the motion of the particle is
Aon a straight line with a constant speed
Bon an ellipse
Cperiodic not SHM
Dsimple harmonic
A particle is moving in a plane with velocity given by $\to u = u_{0} ˆ i + (a ω cos ω t) ˆ j$ , where $ˆ i$ and $ˆ j$ are unit vectors along x and y axes respectively. If particle is at the origin at $t = 0$ . Calculate the trajectory of the particle :-
A $y = a sin (\frac{u_{0}}{ω x})$
B $y = a sin (\frac{ω x}{u_{0}})$
C $y = \frac{1}{a} . sin (\frac{u_{0}}{ω x})$
D $y = \frac{1}{a} . sin (\frac{ω x}{u_{0}})$