Consider the situation as shown in the figure.
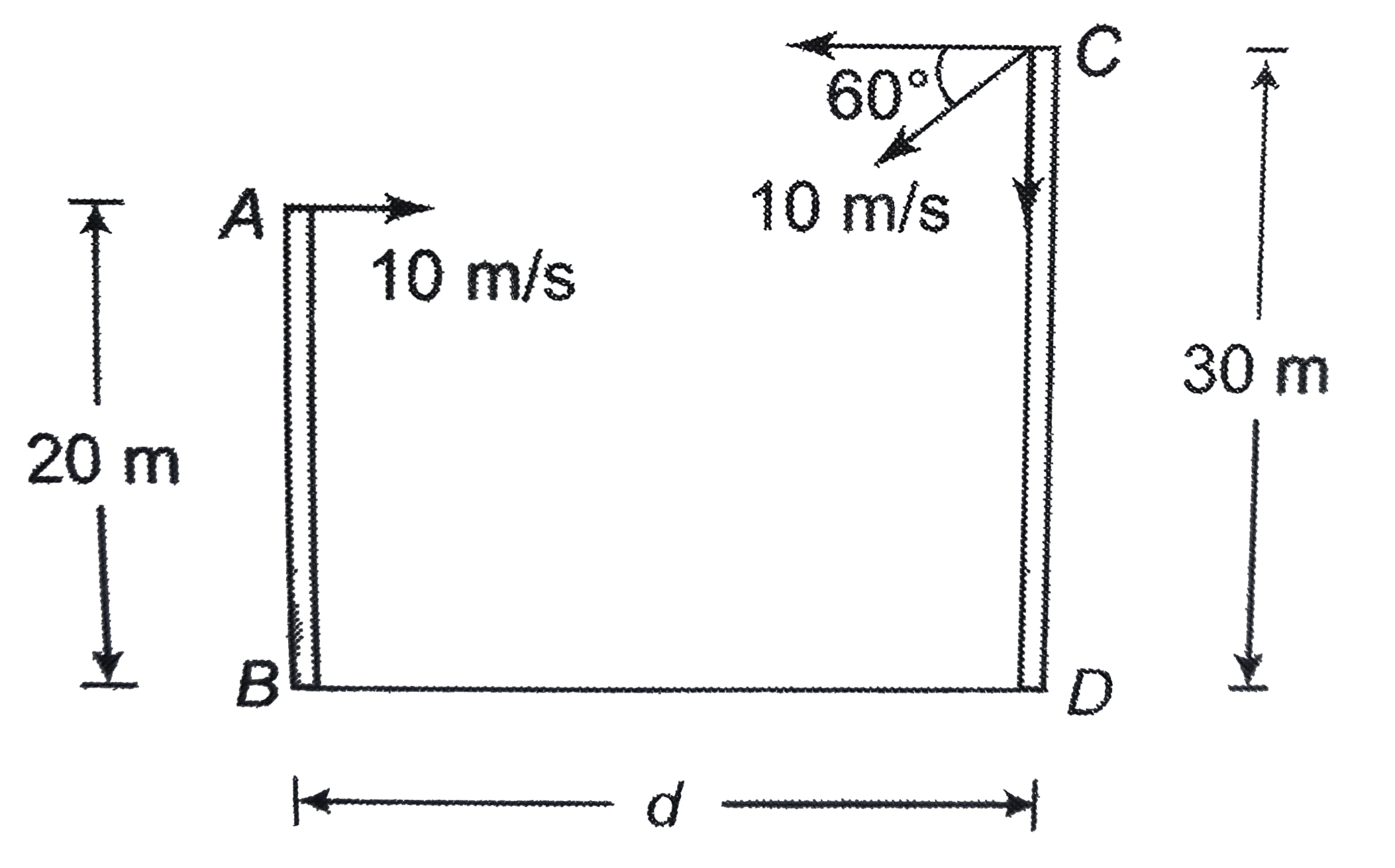
Two balls are thrown simultaneously with same speed 10m/s, one horizontally and another at angle 60∘ in downward direction. After sometime balls cllide in mid-air, find distance d.
Taking B as origin, let the balls collide after time t and at point P(x,y).
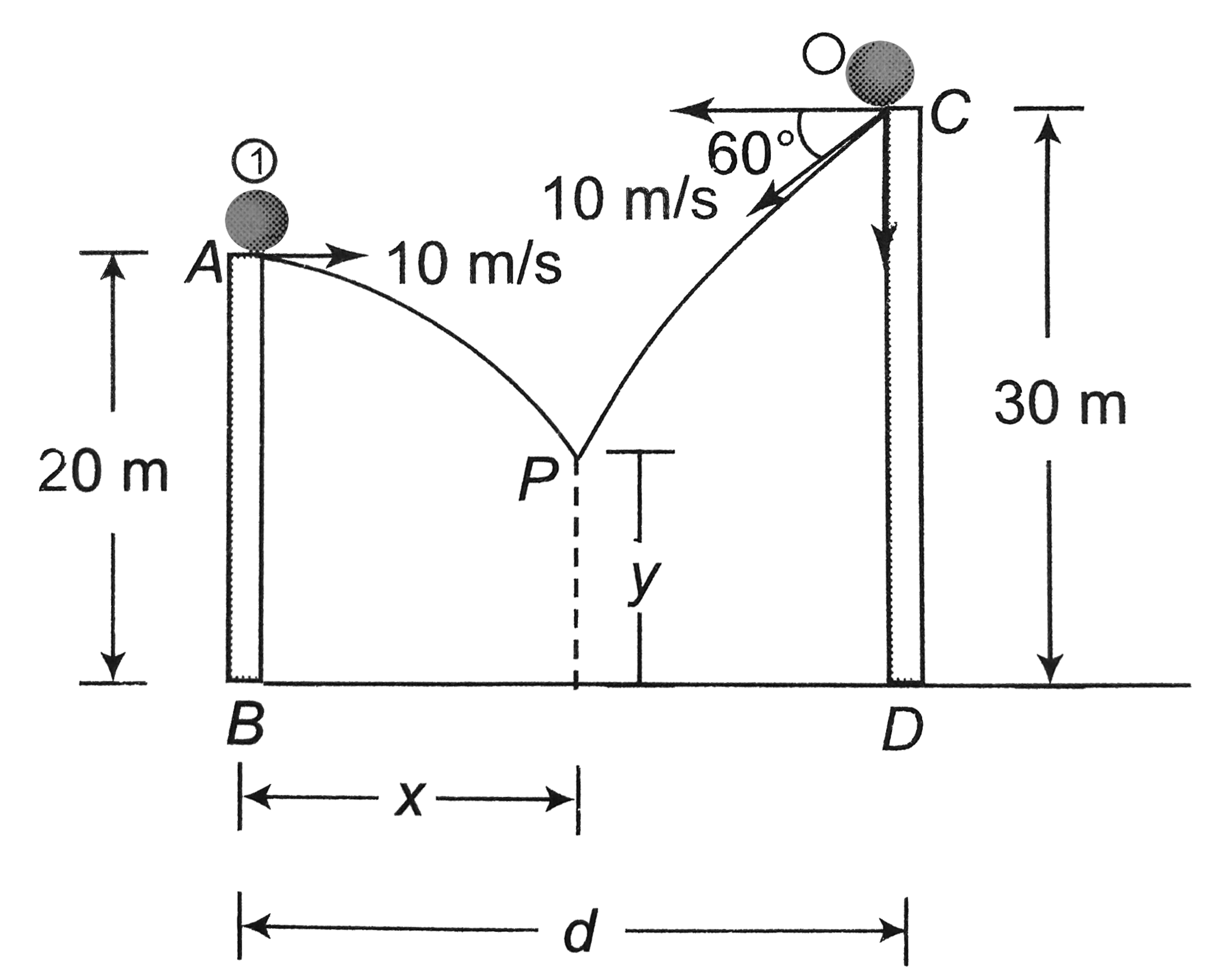
Ball (1): x=10t (i)
y=20−12gt2 (ii)
Ball (2): d−x=10cos60∘t
(iii) y=30−{10sin60∘t+12gt2}
(v) Equating (ii) and (iv), we get
20−12gt2=30−{10sin60∘t+12gt2}
20=30−10√32t⇒t=2√3s
Adding (i) and (iii), we have
d=10t+10cos60∘t
d=15t=15×2√3=30√3=10√3m
Topper's Solved these Questions
Similar Questions
Two balls are thrown up simultaneously from the top of a 400m high tower with speed 10m/s and 55m/s. Sketch a graph showing the separation between the balls versus time.
View SolutionTwo balls of different masses are thrown vertically upwards with the same speed . They pass through the point of projection in their downward motion with the same speed ( Neglect air resistance ).
View Solution
Knowledge Check
- Question 1 - Select One
A ball is thrown with speed 40m/s at an angle 30∘ with horizontally from the top of a tower of height 60m. Choose the correct option
Athe vertical component of velocity first decreases to zero and then increasesBthe ball reaches the ground after 6sCif the ball strikes the ground at maximum horizontal distance from the tower for this the angle of projection should be less than 45∘Dall option are correct - Question 2 - Select One
Two bodies of the same mass are thrown with equal speed from the top of a tower simultaneously. One body (x) 1s thrown vertically downwards. The other (y) is thrown horizontally.
ABoth reaches ground with same Kinetic energyBx reaches-ground with greater Kinetic energyCy reaches ground with greater Kinetic energyDBoth xand y reaches ground simultaneously - Question 3 - Select One
A ball is thrown horizontally with a speed of 20m/s from the top of a tower of height 100m
Horizontal distance travelled by the before it strickes the ground isA10√5mB20√5mC30√5mD40√5m
A ball is dropped from the top of a tower. After 2s another ball is thrown vertically downwards with a speed of 40m/s. After how much time and at what distance below the top of tower the balls meet?
View SolutionThree identical balls are thrown from the top of a building, all with the same initial speed. As shown in figure., the first ball is thrown horizontally, second above horizontal level, and third at an angle below the horizontal. Neglecting air resistance, rank the speeds of the balls at the instant each hits the ground.
 View Solution
View SolutionTwo balls of different masses (one lighter and other heaver) are thrown vertically upwards with the same speed. Which one will pass through the point of projection in the downward direction with greater speed?
View SolutionA ball of mass m is thrown at an angle of 45∘ to the horizontal,, from the top of a 65m high tower AB as shown in Fig. at t=0. Another identical ball is thrown with velocity 20m/s horizontally towards AB from the top of a 30m high tower CD1s after the projection of the first ball. Both the balls move the same vertical plane. If they collide in mid-air,

the height from the ground where the two balls will collide isView SolutionA ball of mass m is thrown at an angle of 45∘ to the horizontal,, from the top of a 65m high tower AB as shown in Fig. at t=0. Another identical ball is thrown with velocity 20m/s horizontally towards AB from the top of a 30m high tower CD1s after the projection of the first ball. Both the balls move the same vertical plane. If they collide in mid-air,

the two balls will collide at time t=View Solution

