
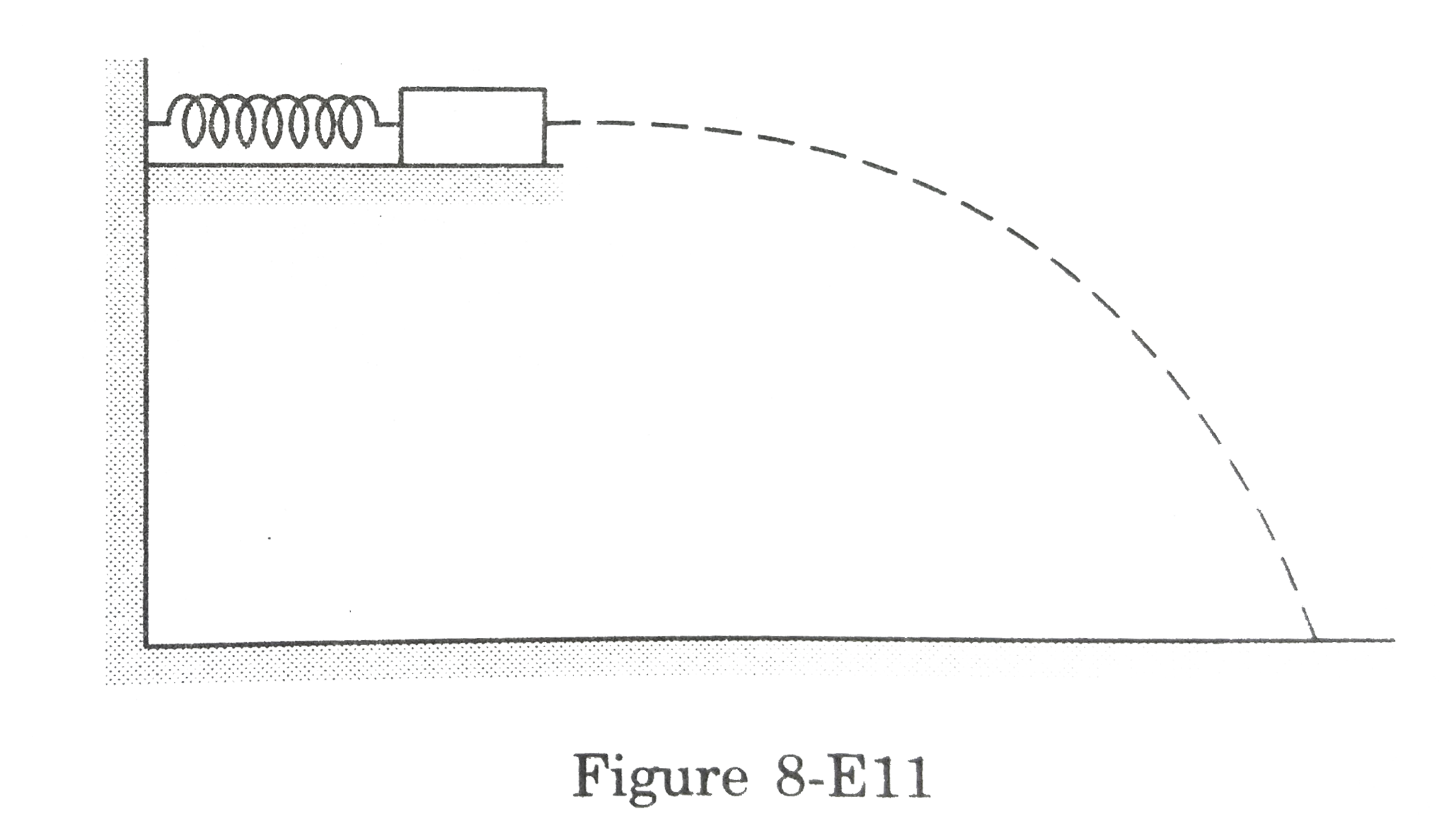
A block of mass is pressed against a horizontal spring fixed at one end to compress the spring through . The natural length of the spring is and spring constant . When released, the block moves horizontally on smooth surface till it leaves the spring. At what horizontal distance from O it strikes the ground.

Between (1) and (2)
A to B (projectile motion)
Topper's Solved these Questions
Similar Questions
A small block of mass 100 g is pressed again a horizontal spring fixed at one end to compress the sprign through 5.0 cm. The spring constant is 100 N/m. When released, the block moves hroizontally till it leaves the spring. Where will it hit the ground 2 m below the spring?
 View Solution
View Solution
A block of mass m is pushed against a spring of spring constant k fixed at one end to a wall.The block can slide on a frictionless table as shown in the figure. The natural length of the spring is L0 and it is compressed to one fourth of natural length and the block is released.Find its velocity as a function of its distance (x) from the wall and maximum velocity of the block. The block is not attached to the spring.View Solution
Knowledge Check
- Question 1 - Select One
A block with mass 0.50kg is forced against a horizontal spring of negligible mass , compressing the spring a distance of 0.20m (figure). When released, the block moves on a horizontal table top for 1.00N/m. What is the coefficient of kinetic friction μk, between the block and the block and the table?
 A0.40B0.50C0.25Dnone of these
A0.40B0.50C0.25Dnone of these - Question 2 - Select One
A block of mass m is pressed against a wall by a spring as shown in the figure. The spring has natural length , l(l>L), and the coefficient of friction between the block and the wall is μ . The minimum spring constant K necessary for equilibrium is:
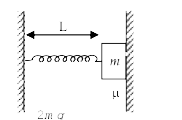 A2mgμ(l−L)Bmgμ(l−L)Cmg2μ(l−L)D2mgμl
A2mgμ(l−L)Bmgμ(l−L)Cmg2μ(l−L)D2mgμl - Question 3 - Select One
A block of mass m is connected at one end of spring fixed at other end having natural length l0 and spring constant K. The block is rotated with constant angular speed (ω) in gravity free space. Find the elongation in spring.
Al0mω2k−mω2Bl0mω2k+mω2Cl0mω2k−mωDl0mω2k+mω
A small block of mass 500 gm is pressed against a horizontal spring fixed at one end to a distance of 10 cm. when released, the block moves horizontally till it leaves the spring. Where it will hit the ground 5 m below the spring. (Take k = 100 N/m of spring)
View SolutionThe ball strikes the block and sticks to it. Find the maximum compression of spring. (L: natural length of spring)
 View Solution
View Solution
A ring of mass m is attached to a horizontal spring of spring constant k and natural length l0. The other end of the spring is fixed and the ring can slide on a horizontal rod as shown. Now the ring is shifted to position B and released Find the speed of the ring when the spring attains its natural length.View SolutionA block of mass M is tied to a spring of force constant k and placed on a smooth horizontal surface. The natural length of the spring is L. P is a point on the spring at a distance L4 from its fixed end. The block is set in oscillations with amplitude A. Find the maximum speed of point P on the spring.
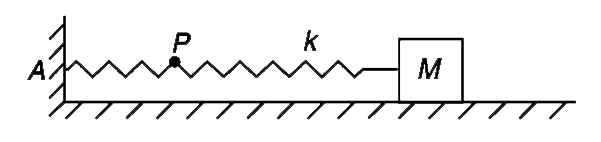 View Solution
View SolutionBlock of mass m is pushed towards a horizontal spring as shown in figure , with initial speed u .

Spring constant of the spring is K and floor is smooth . Calculate maximum possible compression of the spring .View Solution

