
A block of mass 200 g is given velocity 2(m)/(s) on a horizontal surface as shown in the figure. Find the maximum compression of spring of spring constant k=100(N)/(m)

Between (1) and (2)
12mv20=12kx20+Wf
=12kx20+μmgx0
v20=kmx20+2μgx0
(2)2=1000.2x20+2×0.5×10x0
100x20+2x0−0.8=0
x0=−2±√(2)2−4(100)(−0.8)200
=−2±√4+320200=−2±18200
=16200=8100=8cm
Topper's Solved these Questions
Similar Questions
In the fig 4.24 a block of mass m moves with velocity v0 toward a stationaly block of a mass M on a smooth horizontal surface. Find the maximum compression in the spring of stiffnesss constant K.
 View Solution
View SolutionA block of mass m moving at a speed v0 compresses a spring of spring constant k as shown in the figure. Find (a) the maximum compression of spring and (b) speed of the block when the spring is compressed to half of maximum compression.
View Solution
Knowledge Check
- Question 1 - Select One
A block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. Two maximum compression in spring is
 A√2mkv0B√mk.v0C√mk.v0Dm2k.v0
A√2mkv0B√mk.v0C√mk.v0Dm2k.v0 - Question 2 - Select One
A bullet of mass 'm' is fired from a gum of mass M with a (muzzle) velocity u. If the cart on which gun is fixed can move on the smooth horizontal floor as shown

Find maximum compression of spring of spring constant (K) isA√MK(mucosθm)B√KM(MucosθM+m)C√MK(mucosθM+m)D√MK(mucosθM) - Question 3 - Select One
A block of mass m is initially moving to the right on a horizontal frictionless surface at a speed v. It then compresses a spring of spring constant k. At the instant when the kinetic energy of the block is equal to the potential energy of the spring, the spring is compressed a distance of :
Av√m/2kBv√m/kCv√m/4kDmv2/4k
Two identical blocks each of mass M=9kg are placed on a rough horizontal surface of frictional coefficient μ=0.1. The two blocks are joined by a light spring and block B is in contact with a vertical fixed wall as shown in figure. A bullet of mass m=1kg and v0=10m/s hits block A and gets embedded in it. Find the maximum compression of spring. (Spring constant =240N/m,g=10m/s2)
 View Solution
View SolutionA block of mass m is moving with an initial velocity v0 towards a stationary spring of stiffness k attached to the wall as shown in figure

a. Find the maximum compression in the spring.
b. Is the work done by the spring negative or positive?View SolutionA block of mass m sliding n a smooth horizontal surface with velocity →v meets a long horizontal spring fixed ast one end and having spring constant k as shown n figure. Find the maximum compression of the spring. Will the velocity of the block be the same as v whenit comes back to the original position shown?
 View Solution
View SolutionA small block of mass 100 g is pressed again a horizontal spring fixed at one end to compress the sprign through 5.0 cm. The spring constant is 100 N/m. When released, the block moves hroizontally till it leaves the spring. Where will it hit the ground 2 m below the spring?
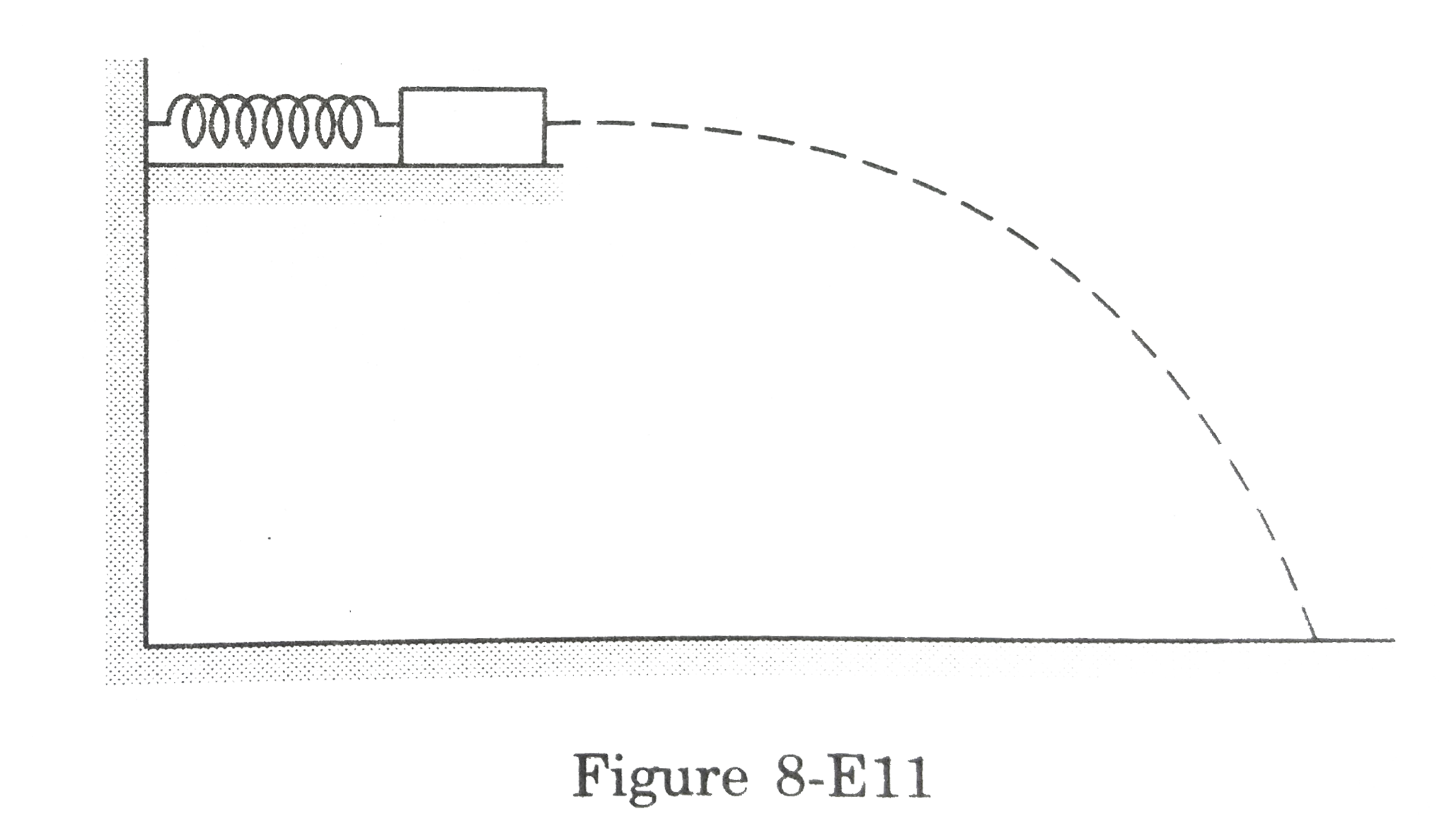 View Solution
View SolutionA block of mass m is moving with a speed v on a horizontal rough surface and collides with a horizontal mounted spring of spring constant k as shown in the figure .The coefficient of friction between the block and the floor is μ The maximum compression of the spring is
 View Solution
View Solution

