A 20 kg body is released from rest so as to slide in between vertical rails and compresses a vertical spring ) placed at a distance m from the strating position of the body. The rails offer a frictional force of 40 N opposing the motion of body. Find (a) the velocity v of the body just before striking with the spring, (b) the maximum compression of the spring and (c ) the distance through which the body is rebounded up.

(a) Between (1) and (2), loss in PE. gain in K.E.work done against friction
(b) Between (2) and (3) loss in P.E. loss in K.E.gain in spring energy work done against friction
(c ) Between (3) and (4):
Topper's Solved these Questions
Similar Questions
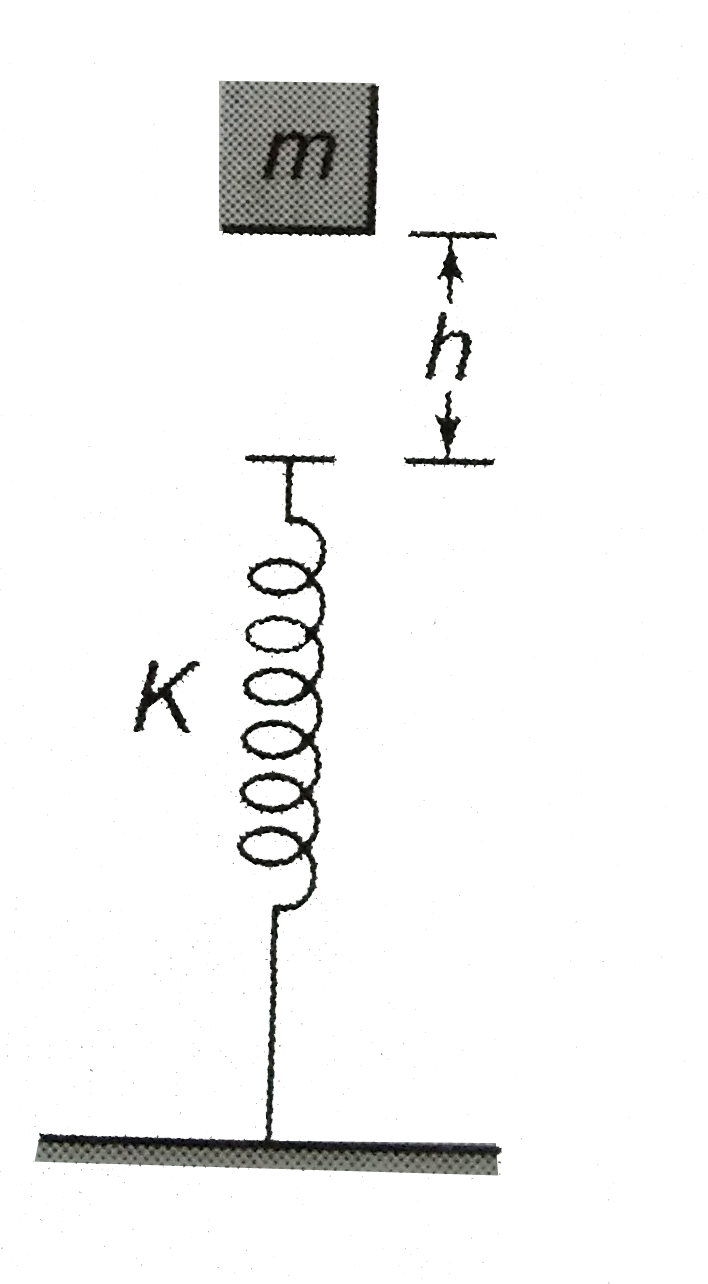
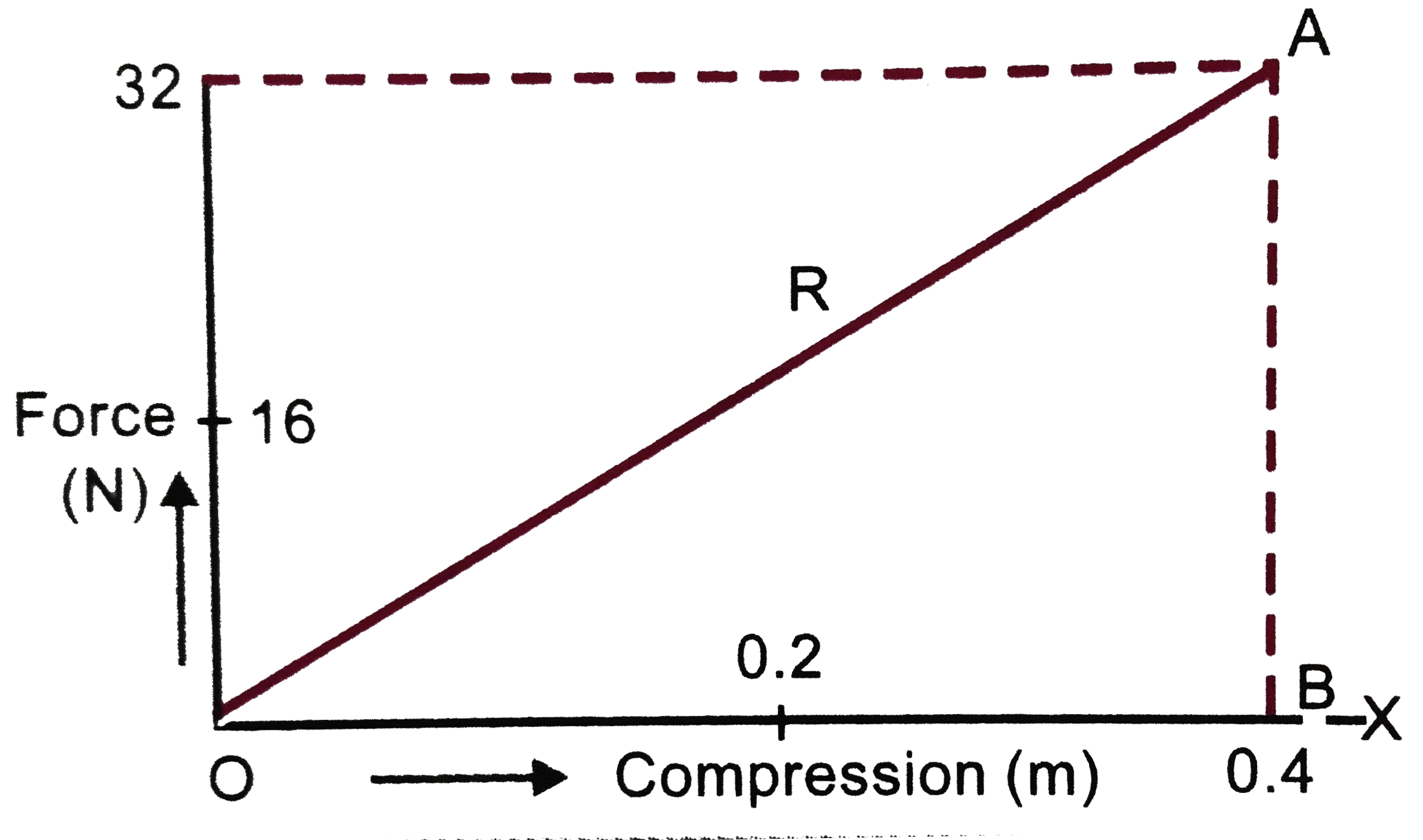
A block is released from height h, find the maximum compression of spring of spring constant k.View SolutionFigure shows a force compression curve of a spring. A body of mass 5kg moving with the velocity of 8m/s hits the spring. Calculate the force constant of the spring and also the compression produced in the spring when the body hits it.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A body of mass m dropped from a certain height strikes a light vertical fixed spring of stifness k. the height of its fall before touching the spring the if the maximum compression of the spring the equal to 3mgk is
A3mg2kB2mgkC3mg4kDmg4k - Question 2 - Select One

A block of mass m initially at rest is dropped from a height h on to a spring of force constant k . the maximum compression in the spring is x thenAmgh=12kx2Bmg(h+x)=12kx2Cmgh=12k(x+h)2Dmg(h+x)=12k(x+h)2 - Question 3 - Select One
A body of mass 0.1 g moving with a velocity of 10 m/s hits a spring (fixed at the other end) of force constant 1000 N/m and comes to rest after compressing the spring. The compression of the spring is
A0.01 mB0.1mC0.2 mD0.5 m
A block of mass m strikes a light pan fitted with a vertical spring after falling through a distance h. If the stiffness of the spring is k, find the maximum compression of the spring.
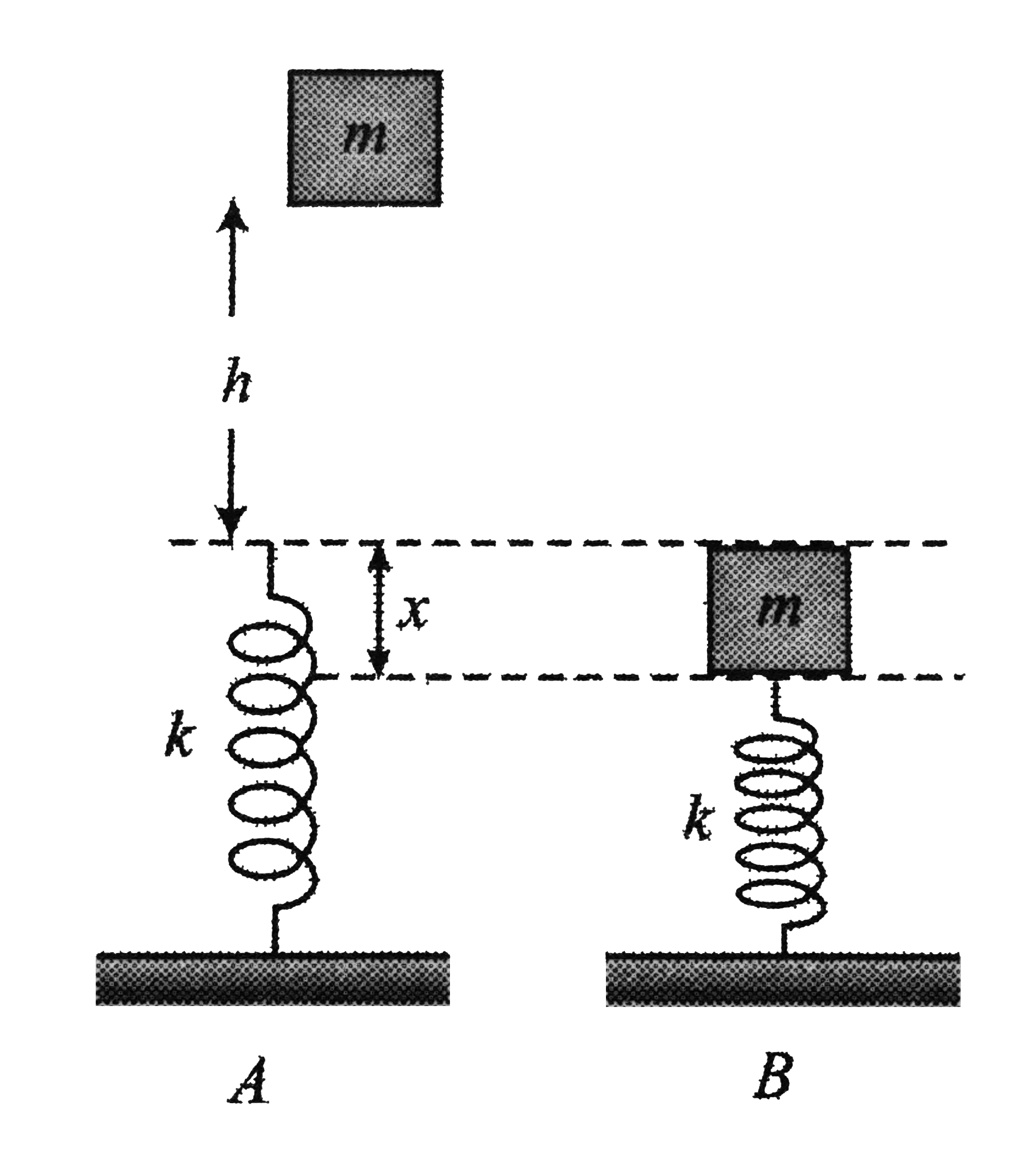 View Solution
View SolutionA spring of spring constasnt 50 N/m is compressed from its natural position through 1 cm. Find the work done by the work done by the spring force on the agency compressing the spring.
View SolutionA body of mass 0.1 g moving with a velocity of 10 m/s hits a spring (fixed at the other end) of force constant 1000 N/m and comes to rest after compressing the spring. The compression of the spring is
View SolutionA body of mass 2 kg is projected vertically upward with a velocity of 2msec−1. The K.E. of the body just before striking the ground is
View SolutionA slab S of mass m released from a height h0, from the top of a spring of force constant k. The maximum compression x of the spring is given by the equation.
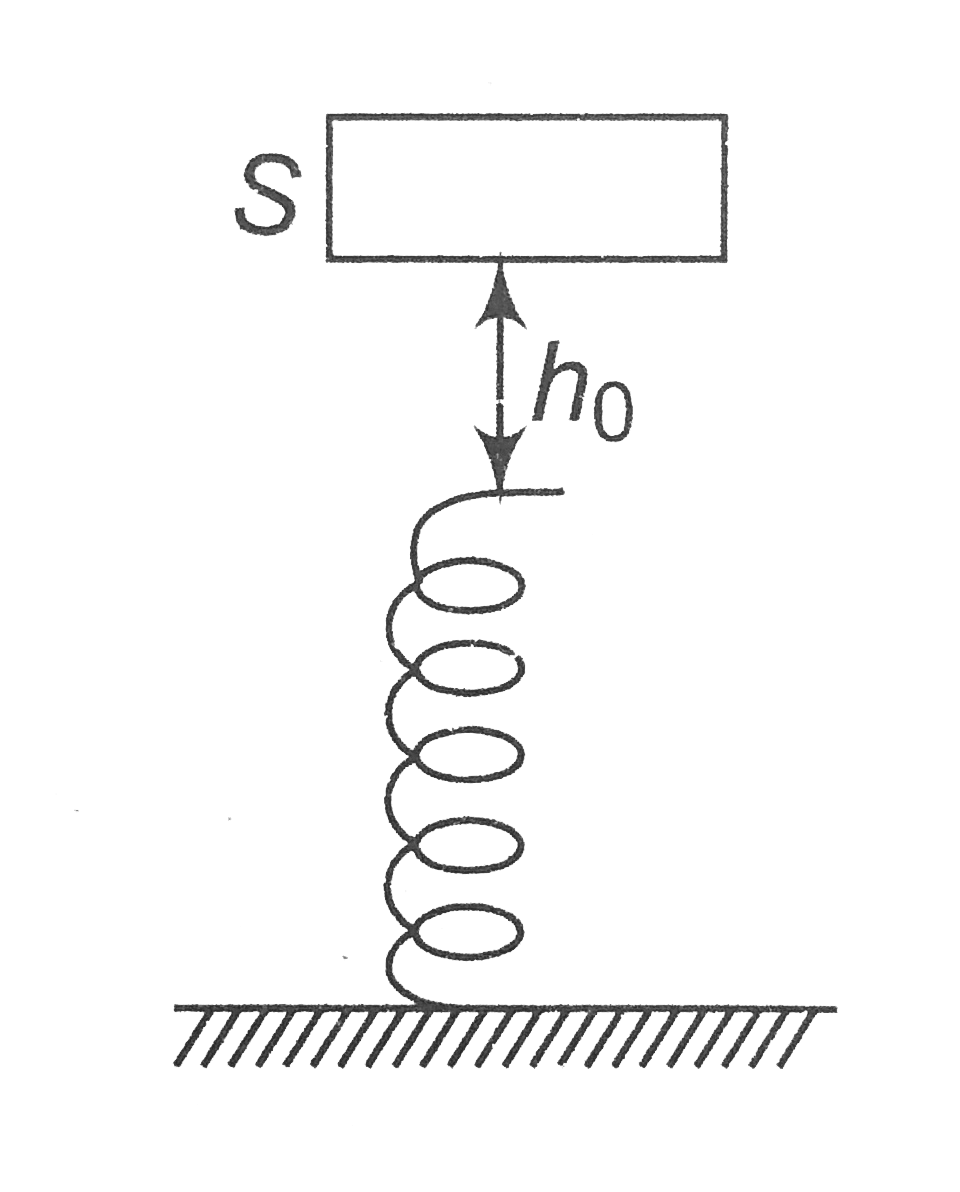 View Solution
View Solution

