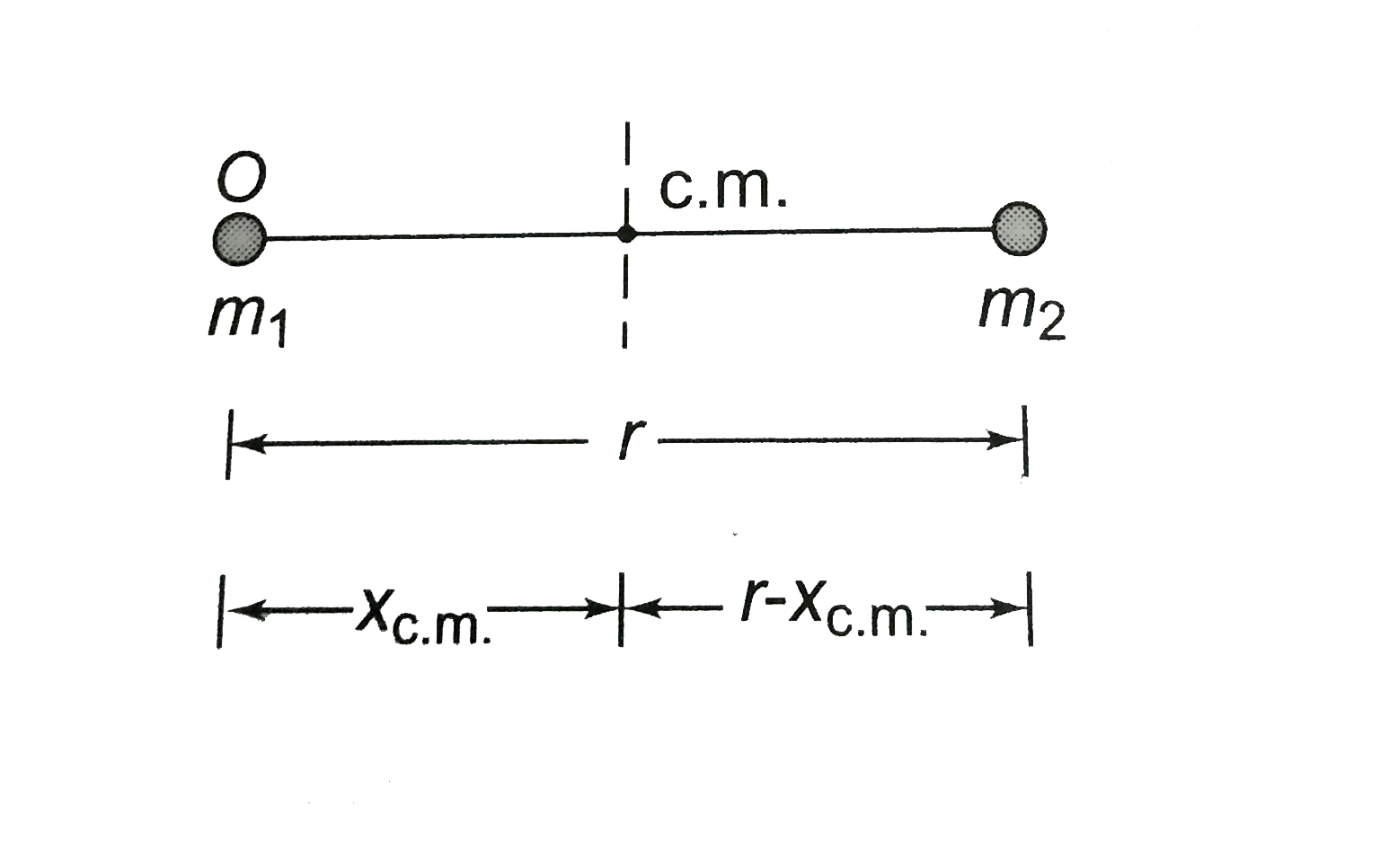
Find the radius of gyration of a system of particles about an axis passing through the center of mass and perpendicular to the line joining the particles. The system consists of two particles of masses $m_{1}$ and $m_{2}$ placed at separation at $r$

Video Solution

Text Solution

Verified by Experts

$x_{c . m .} = \frac{m_{1} \times 0 + m_{2} r}{m_{1} + m_{2}} = \frac{m_{2} r}{m_{1} + m_{2}}$
$I_{A} = m_{1} x_{c . m .}^{2} + m_{2} {(r - x_{c . m .})}^{2}$
$= \frac{m_{1} m_{2}}{m_{1} + m_{2}} r^{2} = (m_{1} + m_{2}) k^{2}$
$k = \frac{\sqrt{m_{1} m_{2}}}{m_{1} + m_{2}} r$

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The position of centre of mass of a system consisting of two particles of masses $m_{1}$ and $m_{2}$ seperated by a distance L apart , from $m_{1}$ will be :
A $\frac{m_{1} L}{m_{1} + m_{2}}$
B $\frac{m_{2} L}{m_{2} + m_{2}}$
C $\frac{m_{2}}{m_{1}} L$
D $\frac{L}{2}$
Question 2 - Select One
Two partcles of masses 1 kg and 2 kg are placed at a distance of 3 m. Moment of inertia of the particles about an axis passing through their centre of mass and perpedicular to the line joining them is (in $k g - m^{2})$
A6
B9
C8
D12
Question 3 - Select One
Two point masses m and 3m are placed at distance r. The moment of inertia of the system about an axis passing through the centre of mass of system and perpendicular to the joining the point masses is
A $\frac{3}{5} m r^{2}$
B $\frac{3}{4} m r^{2}$
C $\frac{3}{2} m r^{2}$
D $\frac{6}{7} m r^{2}$

CP SINGH-ROTATIONAL MOTION-Exercise

Home
Ask Doubt
Profile