A pulley in the form of solid disc of mass $5 k g$ and radius $1 m$ is rotating at an angular speed of 120 rpm when the motor is turned off, Neglecting the friction at the axle, calculate the force that must by applied tangentially to the pulley to bring it to rest in 4 revolutions.

Video Solution

Text Solution

Verified by Experts

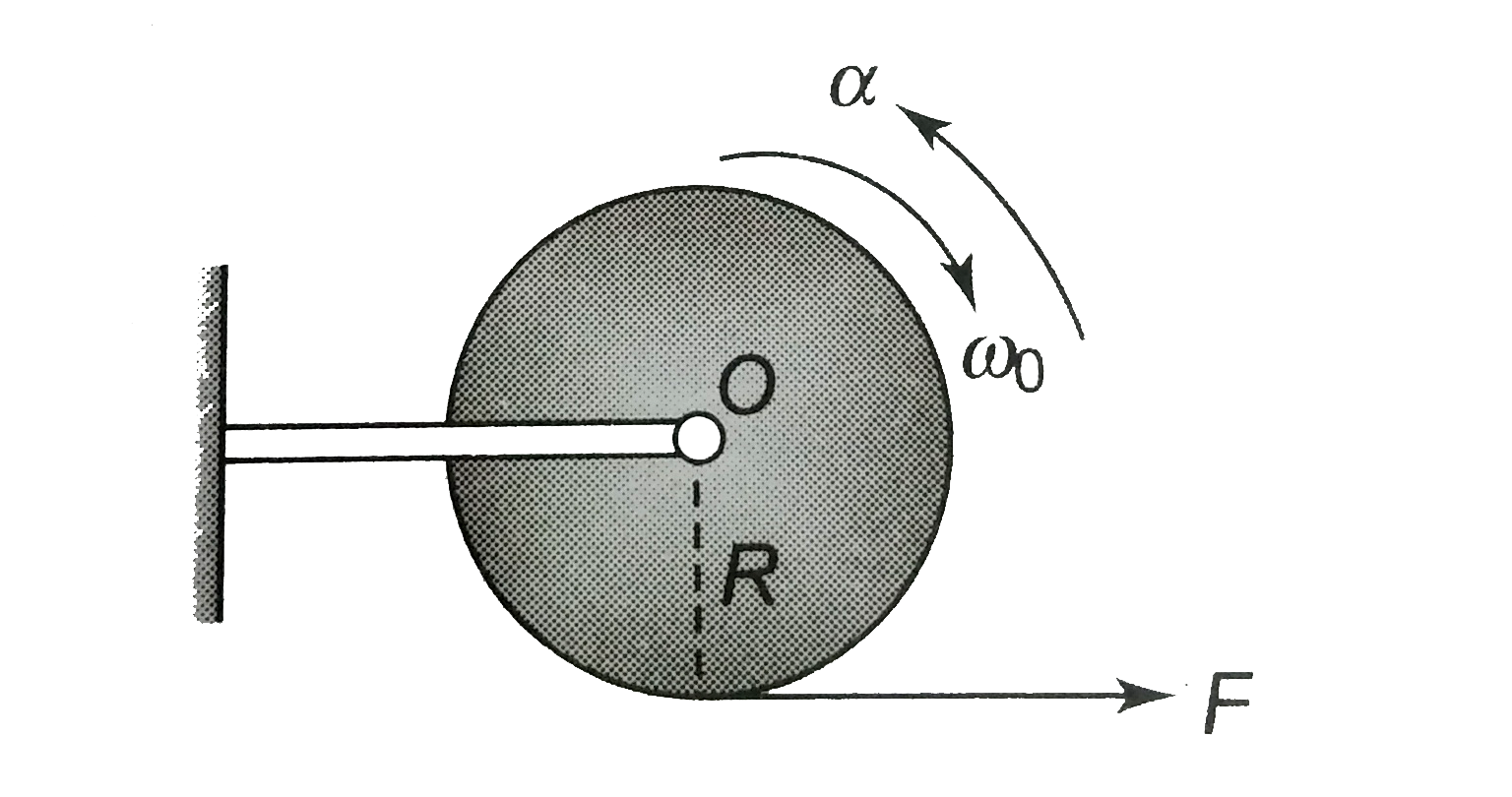
$ω_{0} = 2 π N = \frac{2 π \times 120}{60} = 4 π r a d / s$
$θ = 4 r e v = 8 π r a d$
$ω^{2} = ω_{0}^{2} - 2 α θ$
$o = {(4 π)}^{2} - 2 α (8 π)$
$\Rightarrow α = π r a d / s^{2}$ (angular retardation)
$τ = I α$
$I = \frac{1}{2} m R^{2} = \frac{1}{2} \times 2 \times {(0.5)}^{2} = 2.5 k g m^{2}$
$τ = F R = I α$
$F \times 1 = 2.5 π \Rightarrow F = 2.5 π N$

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A disc of mass M kg and radius R metre is rotating at an angular speed of $ω$ rad/s when the motor is switched off. Neglecting the friction at the axie, the force that must be applied tangentially to the wheel to bring it to rest time t is
A $\frac{M R ω}{2 t}$
B $\frac{M R ω}{t}$
C $\frac{2 M R ω}{t}$
D $\frac{M R^{2} ω}{2 t}$
Question 2 - Select One
A whel of mass 2kg an radius 10 cm is rotating about its axis at an angular velocity of $2 π r a d / s$ the force that must be applied tangentially to the wheel to stop it in 5 revolutions is
A $3 π \times 10^{- 2} k g - m^{2} / s$
B $4 π \times 10^{- 2} k g - m^{2} / s$
C $π \times 10^{- 2} k g - m^{2} / s$
D $2 π \times 10^{- 2} k g - m^{2} / s$
Question 3 - Select One
A flywheel is in the form of solid circular wheel of mass 72 kg and radius of 0.5 m and it takes 70 rpm, then the energy of revolution is
A24 J
B2.4 J
C240 J
D2400 J

CP SINGH-ROTATIONAL MOTION-Exercise

Home
Ask Doubt
Profile