Consider a vehicle taking turn on the horizontal curve with speed v. If the distance between wheels is 2m, height of center of mass above road is 1m and radius of circle is 57.6m, find the maximum value of v for no overturning.
Here 2a=2⇒a=1m
h=1m
R=57.6m
Maximum speed for no overturning
vmax=√gRah=√10×57.6×11=24m/s
Topper's Solved these Questions
Similar Questions
Two wires ACandBC are tied at C of small sphere of mass 5kg which revolves at a constant speed v in the horizontal circle of radius 1.6m Find the maximum value of v
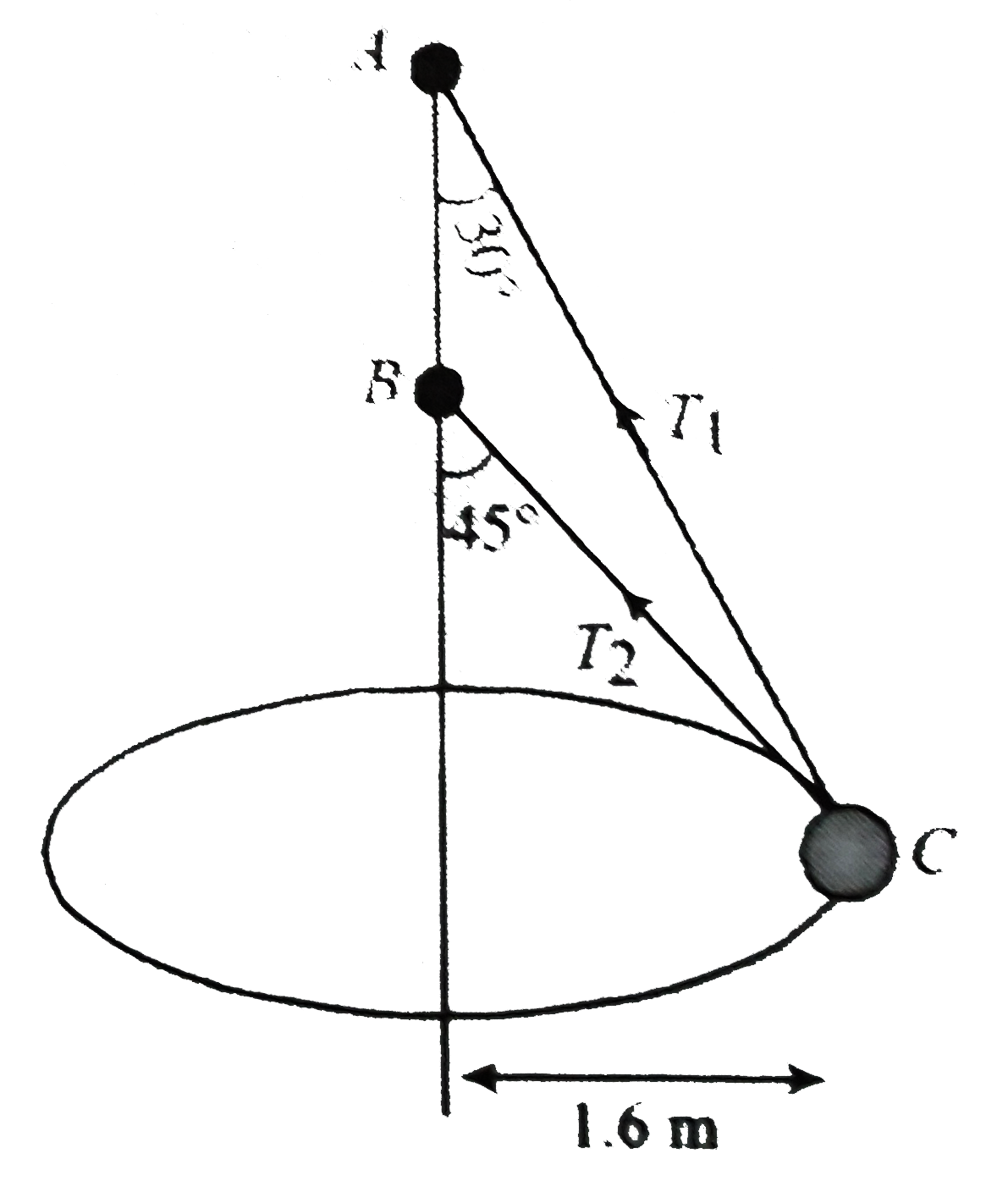 View Solution
View SolutionA car of mass m travelling at speed v moves on a horizontal track. The centre of mass of the car describes a circle of radius r. If 2a is the separation of the inner and outer wheels and h is the height of the centre of mass above the ground, show that the limiting speed beyond which the car will overturn in given by
v2=grah
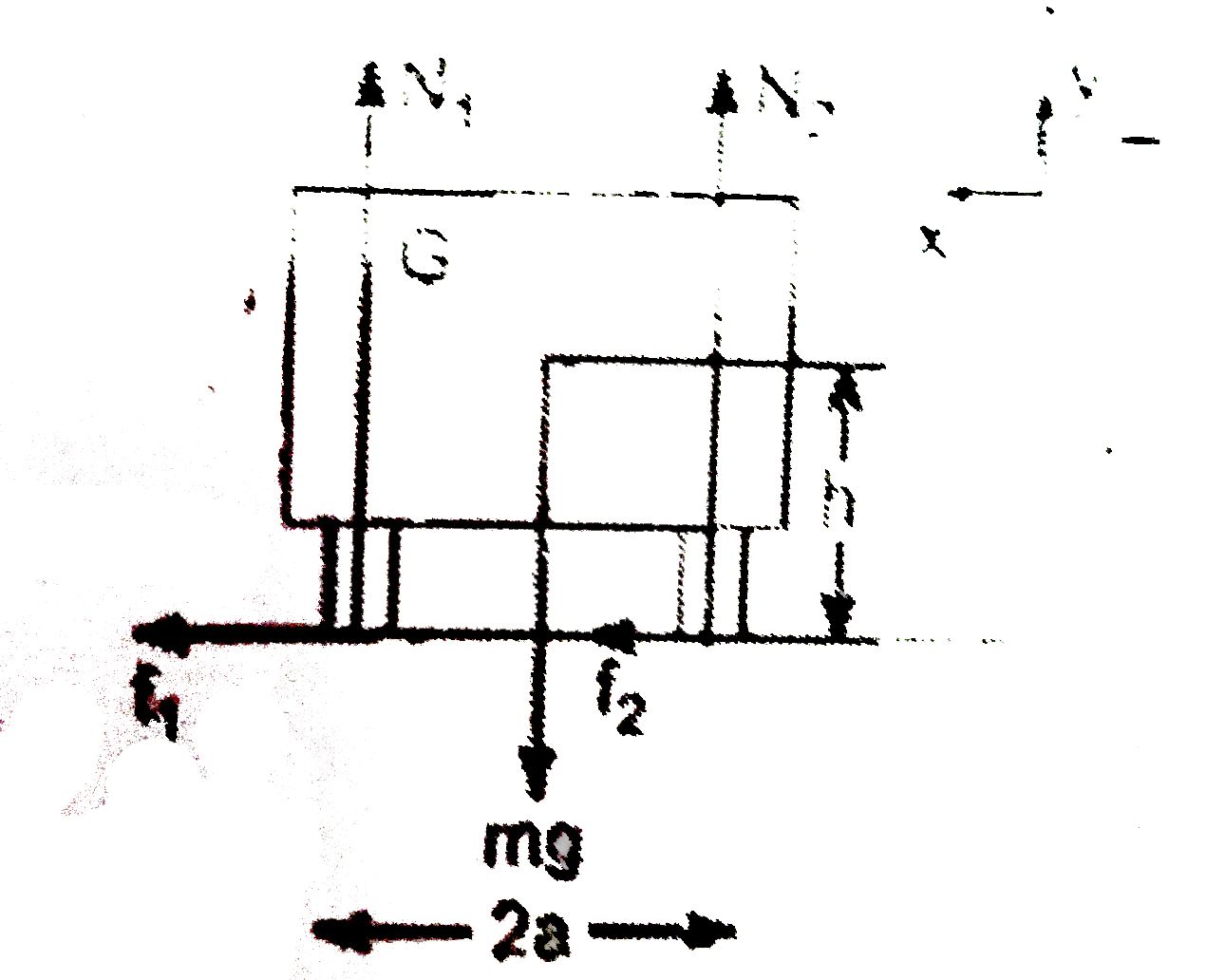 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The height of a T.V. tower is 100m. If radius of earth is 6400km, then what is the maximum distance of transmission from it ?
A100kmB64√10kmC6.4√10kmD8√20km. - Question 2 - Select One
A vehicle of mass M is moving on a rough horizontal road with a momentum P If the coefficient of friction between the tyres and the road is μ is then the stopping distance is .
AP2μMgBP22μMgCP22μM2gDP22μM2g - Question 3 - Select One
A vehicle of mass M is moving on a rough horizontal road with a momentum P. If the coefficient of friction between the tyres and the road is μ, then the stopping distance is
AP2μMgBP22μMgCP22μM2gDP2μM2g
The CG of a loaded truck is at a height of 3 m above the ground and the distance between its wheels is 3m. What is the maximum speed with which it can go round a curved road of radius 200 m without turning turtle ?
View SolutionA vehicle of mass m is moving on a rough horizontal road with momentum p. If the coefficient of friction between the tyres and the road be μ, then the stopping distance is
View SolutionA vehicle of mass m is moving on a rough horizontal road with momentum P . If the coefficient of friction between the tyres and the road br mu, then the stopping distance is:
View SolutionA vehicle moves on a horizontal curved road of radius of curvature 50 m height of centre of gravity 1.5 m the distance between the two wheels 2 m and acceleration due to gravity 9.8m/s2 . Then the maximum velocity with which it can travel on the road will be
View SolutionA car moves with speed v on a horizontal circular track of radius R. A head-on view of the car is shown in figure. The height of the car's centre of mass above the ground is h, and the separation between its inner and outer wheels is d The road is dry, and the car does not skid. The maximum speed the car can have without overturning is :
 .View Solution
.View Solution

