Two balls of masses $m$ and $2 m$ are attached to the ends of a light rod of length $L$ . The rod rotates with an angular speed $ω$ about an axis passing through the center of mass of system and perpendicular to the plane. Find the angular momentum of the system about the axis of rotation.

Video Solution

Text Solution

Verified by Experts

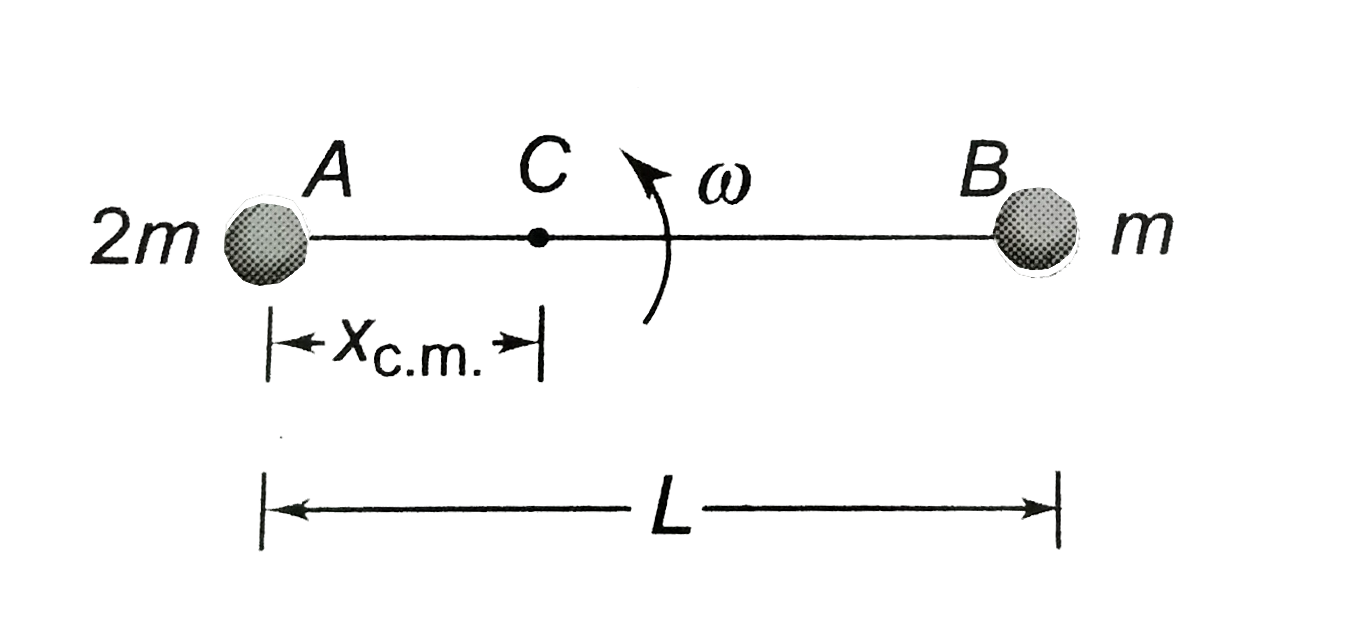
Location of $c . m .$
$x_{c . m .} = (2 m \times 0 + m \times L) (2 m + m) = \frac{L}{3}$
The velocity of ball $A$ w.r.t the center of mass $C$ is
$v_{A} = ω x_{c . m .} = \frac{ω L}{3}$
$v_{B} = ω (L - x_{c . m .}) = \frac{2 ω L}{3}$
Angular momentum of a system about $C$
$L = 2 m v_{A} x_{c . m .} + m v_{B} (L - x_{c . m .})$
$= 2 m \times \frac{ω L}{3} \times \frac{L}{3} + m \times \frac{2 ω L}{3} \times \frac{2 L}{3}$
$= \frac{2 m ω^{2} L}{3}$
OR
$L = I_{c . m .} ω = [2 m x_{c . m .}^{2} + m {(L - x_{c . m .})}_{c . m .}^{2}] ω$
$= [2 m {(\frac{L}{3})}^{2} + m {(\frac{2 L}{3})}^{2}] ω = \frac{2 m ω^{2} L}{3}$
Note: For a particle moving in a circle is as follows.

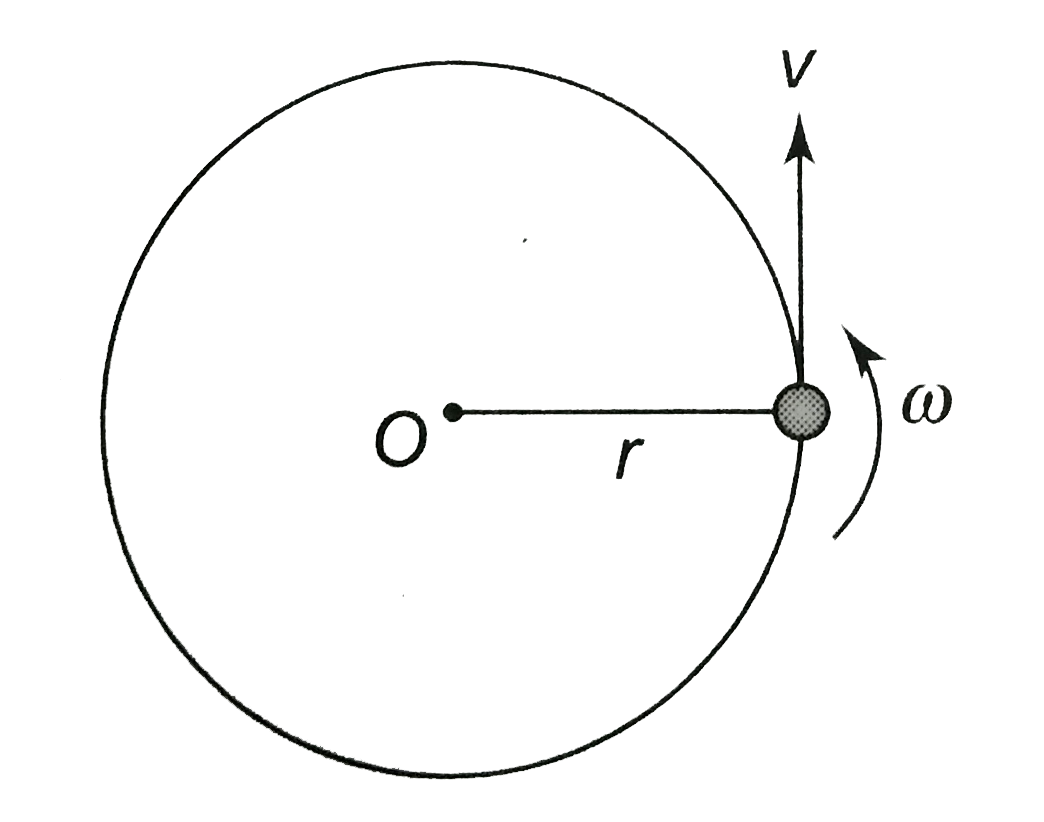
Angular momentum of particle about $O$
$L_{0} = m v r = m (r ω) r = m r^{2} ω$
OR
$L_{0} = I_{0} ω = m r^{2} ω$

Updated on:21/07/2023

Two particles, each of mass m and charge q are attached to the two ends of a light rigid rod of length 2R. The rod is rotated at constant angular speed about a perpendicular axis passing through its centre. The ratio of the magnitudes of the magnetic moment of the system and its angular momentum about the centre of the rod is
A $\frac{q}{m}$
B $\frac{2 q}{m}$
C $\frac{q}{2 m}$
D $\frac{q}{π m}$
Two particles , each of mass $m$ and charge $q$ , are attached to the two ends of a light rigid rod of length $2 R$ . The rod is rotated at constant angular speed about a perpendicular axis passing through its centre. The ratio of the magnitudes of the magnetic moment of the system and its angular momentum about the centre of the rod is
A $\frac{q}{2 m}$
B $\frac{q}{m}$
C $\frac{2 q}{m}$
D $\frac{q}{π m}$
Two masses each of mass $M$ are attached to the end of a rigid massless rod of length $L$ . The moment of interia of the system about an axis passing centre of mass and perpendicular to its length is.
A $\frac{M L^{2}}{4}$
B $\frac{M L^{2}}{2}$
C $M L^{2}$
D $2 M L^{2}$